Article contents
A Numerical Method of Finding a Suitable Bonus Scale
Published online by Cambridge University Press: 29 August 2014
Extract
The bonus system used by Finnish insurers is as follows: Policies are divided into 4 bonus classes, C1, C2, C3, C4, each of them being initially placed in class C1. After one claimless year, a policy placed in class Ch is transferred to class Ch+1 (h ≤ 3) from the beginning of the following year. After a claim year, each policy is entered back to class C1. (Whether the number of claims is one or more does not play any role in this transition system.) From the initial premium, i.e. the premium in class C1, a reduction of pi, per cent is granted in class Ci. In numbers these percentages are as follows: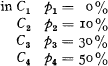
In present investigations there is a trend to replace this scale by another in which mere contingency would not cause too great a change in the premium and in which the „test period” would be longer.
Let us suppose that we want to find a suitable percentage scale P = (P1, P2, …, Pm) for a bonus system (Cl, C2, …, Cm) with a given transition mechanism according to which for each bonus class Ch two bonus classes Ci and Cj are given to which the policy is transferred after one year from Ch according as there have been claims or not.
Information
- Type
- Problems in Motor Insurance
- Information
- Copyright
- Copyright © International Actuarial Association 1962
References
- 9
- Cited by

