Article contents
Driving with markov-programming
Published online by Cambridge University Press: 29 August 2014
Extract
Let us consider the following problem.
A motorist has decided to effect an accident insurance under the following conditions. The insurance runs for one year. The premium for the first year amounts E0. If no damages have been claimed during i successive years, i = 1, 2 or 3 the premium is reduced to Ei. After four years of damagefree driving no further premium reduction is granted, so the premium remains E3. The premium is due on the first day of the year. The own risk amounts a0.
The number of accidents of our motorist during a time period T is assumed to be Poisson distributed with parameter λT. The extent of the damage 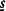 has distribution function F(s) with finite mean and variance.
has distribution function F(s) with finite mean and variance.
The problem of our motorist will be to decide whether to claim a damage or not. He will have to develop a strategy that specifies his decisions in every possible situation. His strategy will be called optimal if it minimizes the expected costs in the long run.
We may expect that in view of the premium reduction, it will be unprofitable to claim damages which are not much larger than a0. Once a damage is claimed it will be profitable to claim all following damages that exceed a0 during the remaining part of the year.
Hence his decisions will also depend on the time of the year and the premium paid at the beginning of that year. So we distinguish between four types of years, for each premium one.
Information
- Type
- Astin Colloquium 1966 Arnhem Subject two
- Information
- Copyright
- Copyright © International Actuarial Association 1968
- 7
- Cited by

