I. INTRODUCTION
Rate control (RC) is an important tool that helps to deal with bit rate and compressed media quality fluctuations. RC methods have been widely studied and suitable schemes have been developed for specific applications [Reference Wu, Xie, Zhang and Wu1]. This problem is also related to challenging issues such as resource availability, computational complexity and real-time [Reference Chen and Ngan2]. More precisely, we consider RC for a specific class of applications, namely video conferencing. In this context, one of the most interesting issues to focus on is the quality enhancement of regions of interest.
Indeed, in various fields such as video conferencing systems, video surveillance, and telemedicine, the subjective visual quality mainly depends on some important areas, called regions of interest (ROIs). Therefore, many contributions have introduced rate control algorithms aiming the improvement of the quality in the ROIs. For example, in [Reference Yang, Zhang, Ma and Zhao3] a rate control scheme based on adjustable quality of the ROI has been proposed. The RC algorithm used the quadratic model implemented in H.264/AVC to compute for each region a quantization parameter (QP) referring to a quality level chosen by the user. The same quadratic model is used in [Reference Chiang, Hsieh, Chang, Jou and Lie4] to compute the QP of each macroblock and then adjust it referring to an input saliency map and to the number of bits allocated to each region. For a video surveillance system, RC in [Reference C.-Wu and P.-Su5] uses a linear rate-quantization (R-Q) model to decide the bit-stream length and then the QP of each region.
A different ROI-based method has been proposed in [Reference Hu, Li, Lin, Li and Sun6]. It uses a macroblock classification based on rate-distortion (R-D) characteristics to generate three kinds of regions (called basic units). A weighted bit allocation per region is performed with predetermined factors in heuristic ways. Finally, a linear rate-quantization stepsize (R-QS) model and a distortion-quantization stepsize (D-QS) model compute a QP per basic unit.
These techniques considered the R-Q linear model [Reference C.-Wu and P.-Su5, Reference Hu, Li, Lin, Li and Sun6] or the quadratic RC model [Reference Yang, Zhang, Ma and Zhao3, Reference Chiang, Hsieh, Chang, Jou and Lie4] and are useful for H.264/AVC implementations. Meanwhile, the new HEVC standard has been recently finalized by ITU-T and ISO/IEC [Reference Sullivan, Ohm, Han and Wiegand7] and many works have focused on rate control and developed new R-Q schemes for it. In the reference software, two different algorithms have been proposed. The first one is based on a quadratic model and the mean absolute difference (MAD) between the original and the reconstructed signal [Reference Choi, Nam, Yoo and Sim8, Reference Choi, Nam, Yoo and Sim9]. In the second algorithm, an R-λ model that takes into account the hierarchical coding structure has been adopted [Reference Li, Li, Li and Zhang10]. This model, initially introduced in HM.10, has been improved in a recent version of the reference software (HM.13). Adaptive bit allocation at the frame level has been introduced [Reference Li, Li and Li11] by considering variable weights for each hierarchical level that depend on video content characteristics. Then, in [Reference Karczewicz and Wang12], intra frame rate control has been modified by enabling basic unit level rate control.
Recent works on high-efficiency video coding (HEVC) have proposed bit allocation approaches that take into account coding units (CUs) texture. In [Reference Lee, Kim and Nguyen13], CUs are classified referring to their depth in the quad tree and their coding type. Texture-based rate models for HEVC have been developed according to signal characteristics in different CU depths and coding types. Rate models for three types of Cus of different texture levels have been constructed to deal with more complex content and to ensure more accurate rate control at the CU level.
All the above-mentioned RC algorithms, which have been developed for HEVC, do not take into account the importance of particular regions of the frame. Therefore, we propose a new rate control scheme for video conferencing systems which processes the faces (ROIs) and the background separately. We propose two versions for this algorithm. The first one is based on the model implemented in the reference software HM.10 [Reference Li, Li, Li and Zhang10] performing the R-λ model on B-frames only. While, the second one considers the modified RC model introduced in HM.13 [Reference Li, Li and Li11] that performs RC for both I and B frames. The reference controller is enhanced with three main features; first, using an object detection method, we detect our ROI and generate automatically a binary map (ROI map). The target bit rate is allocated for each region considering a fixed weight. Then, the QP of each coding tree unit (CTU) is computed referring to the rate model of the corresponding region and the allocated bit budget. Finally, the proposed method considers independent R-D models for each region and different clipping values for QP variation, taking into account the importance of each part of the image. Overall, we show that the quality of the ROI is improved and the bit rate limit is respected. The proposed method has been compared to the ROI-based controller described in [Reference Chiang, Hsieh, Chang, Jou and Lie4]. This algorithm based on a quadratic representation of the R-D model was implemented and tested for H.264/AVC. In our work, we adapt it to HEVC, implement it in HM.9 and compare its performance to our approach.
The paper is organized as follows. Section II introduces different methods for ROI detection and describes the general rate control problem. Then, Section III briefly reviews the main features of rate control for HEVC based on the R-λ model, compares it to the quadratic model and studies the evolution of the controller. The proposed algorithm is explained and detailed in Section IV. Moreover, the main modification of the adopted controller are detailed. In Section V, the experimental results related to both HM.10 and HM.13 integrations are presented and the controller implemented in HM.9 is evaluated. Finally, conclusions and future research directions are given in Section VI.
II. RELATED WORKS
A) ROI detection algorithms
Many algorithms have been proposed for automatic ROI detection. They can be classified into two categories: bottom-up methods assume that human eyes skirt rapidly across the entire image and select small areas, while top-down methods suppose that people pay more attention to areas corresponding to semantic objects of the image [Reference Chuang, Cheng and Yung-Yu14]. Top-down approaches mainly consist in generating a saliency map taking into account the importance of semantic objects such as text, faces, eyes, etc.
One of the earliest works in face detection is a real-time system developed in [Reference Zahir, Samad and Mustafa15] to emphasize the face region. The proposed method is based on a shape recognition algorithm. The system is able to detect and track human faces considering skin color segmentation and contour evaluation.
Viola and Jones object detector [Reference Viola and Jones16] is a famous and successful tool, widely used for face detection. For specific applications, such as video conference or supervision systems, this algorithm is appropriate as it has shown strong power in detecting faces, while for other applications, some improvements have been introduced to Viola and Jones algorithm by introducing new feature images. This framework used a set of Haar-like features in which each characteristic was described by a template. OpenCV library has included different implementations of Viola and Jones object detector algorithm [Reference Li, Niaz and Merialdo17].
In our work, as we focus on video conferencing systems, we used OpenCV library for face detection and ROI map generation. We do not aim at making a perfect segmentation of the face at the pixel level. The generated mask is done at the CTU level. Thus, a binary mask is generated to register if each CTU of the frame belongs to the ROI or not.
B) RC theory
The objective of RC is to achieve a target bit rate as close as possible to a given constant while ensuring minimum quality distortion. Knowing that quantization consists in reducing the bit rate of the compressed video signal, the major role of RC algorithms is thus to find for each transform coefficient the appropriate QP under the constraint R s (QP) ≤ R max . The fixed bit budget is R max and R s (QP) is the number of coding bits for the source sample s. If we note D s the distortion measure between the original and the constructed samples, the problem can be formulated as:
In video coding, RC usually incorporates rate-distortion optimization (RDO). Knowing the QP given by the rate control, RDO consists in minimizing the cost
to achieve the optimized mode decision of each CU. Using a Lagrange multiplier λ MODE in (2), the distortion D(QP) is associated with the number of bits R(QP) to evaluate all possible coding modes and select the one minimizing J [Reference Sullivan and Wiegand18, Reference Wiegand, Schwarz, Joch, Kossentini and Sullivan19].
Consequently, these problems need explicit models that relate the average bit rate to the QP. Several works have therefore been done in perceptual quality, for estimating the distortion, and in rate modeling. Different rate models have been developed, some of them based on simple linear expressions, others on more complex mathematical representations. For example, in [Reference Ma, Si and Wang20], the traditional linear model that was employed in TM5 for high bit rate video coding is studied for HEVC:
where C is the model parameter. The quadratic model represented as
where C 1 and C 2 are the model parameters and the MAD is the MAD between the original frame and the reconstructed one [Reference Choi, Nam, Yoo and Sim8]. This model has been adopted in VM8 for MPEG4 [Reference Yu and Ahmad21], H.264/AVC [Reference Li, Gao, Pan, Ma, Lim and Feng22], and also for HEVC [Reference Naccari and Pereira23].
The accuracy of these models has been enhanced by introducing the so-called complexity of the source, using the per pixel gradient value in the R-Q model in [Reference Sun, Au and Dai24]. The sum of absolute transformed differences (SAD) has been adopted in [Reference Si, Ma and Gao25]. In a different way, the RC was improved by considering a representation in the ρ domain [Reference Yoon, Kim, Jung and Jun26] as proposed in [Reference He and Mitra27] and by taking into account additional parameters, like the frame rate [Reference Ma, Xu, Ou and Wang28].
The most recent R-D model in the HEVC reference software is the R-λ model expressed as follows:
where α and β are the model parameters [Reference Li, Li, Li and Zhang10]. We note that this model defines a relationship between the rate in bits per pixel, R, and the Lagrange parameter λ which is used in RDO to decide the coding mode. Using this R-λ model, λ is generated first, and then the QP at the frame level is computed. In our work, this model has been adopted for the frame level bit allocation and modified for our video conferencing system.
C) ROI and rate control
With rapid demands for ROI in applications like video conferencing, video surveillance and telemedicine, ROI-based rate control has gained increasing attention from researchers [Reference Yang, Zhang, Ma and Zhao3–Reference Hu, Li, Lin, Li and Sun6]. All these works are based on the controller implemented in the H.264/AVC reference software.
In [Reference Yang, Zhang, Ma and Zhao3], an ROI quality adjustable rate control algorithm has been proposed. Bit allocation is initially done according to user's interest level and available budget. The proposed quadratic R–D model defined in (4) considers the bit rate constraint and possible quality levels to define a QP margin. A number of bits is then allocated for each region and the QP is refined. In this scheme, ROI is processed first, and then the non-ROI areas. A QP is assigned for each region.
In [Reference Chiang, Hsieh, Chang, Jou and Lie4], the same quadratic model is used and again faces are considered as ROIs. However, new features are introduced in this proposition. First, human psychovisual clues are used to compute a saliency map for each frame, which is used for rate control. A quality factor is defined and the bit budget is allocated for ROI and non-ROI separately. Finally, the quadratic model is used to assign a QP for each region considering a clipping range for smooth visual quality along the temporal direction and across region boundaries.
In [Reference C.-Wu and P.-Su5], an ROI-based rate control was designed for traffic surveillance systems. A fast ROI extraction method for the real-time video compression is used to generate the ROI map. A linear function has expressed the relation between the bit-stream length and the quantization step (3). This model helps to predict the frame level bit allocation and the region level QP determination. In this work, the model is used for each block. Thus, a QP is computed for each macroblock.
In [Reference Hu, Li, Lin, Li and Sun6], a complete ROI-based controller is proposed. The scheme includes five steps, starting with region devising using the R-D characteristics of each macroblock. Macroblocks with similar characteristics are classified in the same basic unit and an overall bit allocation is performed using two linear models (R-QS and D-QS). A QP is computed for each basic unit. Finally, RDO is performed for each macroblock and models' parameters are updated as done in previous propositions.
The above-mentioned algorithms provide a bit rate repartition that takes into account the high priority of the ROI. They have been developed considering linear and quadratic models and implemented in the H.264/AVC JM software. In this paper, we propose a new ROI-based rate control scheme for HEVC characterized by several features. First, face detection is performed using Viola and Jones algorithm [Reference Viola and Jones16], an ROI map is generated and an ROI and non-ROI bit partition is determined accordingly. Second, the proposed model is used separately for ROI and non-ROI. Finally, a QP is assigned for each unit and clipped to keep quality smoothness.
The RC algorithm proposed in [Reference Chiang, Hsieh, Chang, Jou and Lie4] is the most appropriate for HEVC. It is possible to adapt it to the HEVC controller, as it uses a quadratic model for QP computing which is not the case in reference [Reference C.-Wu and P.-Su5] and keeps processing blocks in encoding order, which is not the case in the reference algorithm [Reference Yang, Zhang, Ma and Zhao3]. Consequently, the proposed ROI-based controller in [Reference Chiang, Hsieh, Chang, Jou and Lie4] has been implemented in HM.9 and compared to our algorithm. A detailed description of these algorithms is given in the next section.
III. RATE CONTROL FOR HEVC
In video coding, controllers have been designed to achieve the main goals of high coding efficiency and accurate matching of the target rate. Our approach aims at providing an ROI-based bit allocation between regions and achieves the controller goals (quality and budget). Thus, it is important to evaluate the key elements of the controller before introducing the ROI constraint. This section briefly describes rate control scheme for HEVC and different options at the frame and CTU levels.
A) R-λ-based rate control
1. R-λ SCHEME
As stated before, each model targets a specific video coding system under particular conditions. However, all the rate control methods aim at allocating the appropriate number of bits and at determining the QP of each CTU. The complete R-λ rate control scheme in HEVC can be represented as illustrated in Fig. 1:
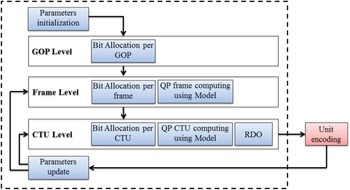
Fig. 1. RC scheme for HEVC.
As it can be seen from this figure, the controller operates at three main levels: group of pictures (GOPs), frame, and CTU [Reference Sullivan, Ohm, Han and Wiegand7]:
-
(i) GOP level: the input parameters are the global target bit rate, the sequence frame rate, the GOP size and the virtual buffer occupancy. The rate control algorithm computes here an average number of bits per GOP.
-
(ii) Frame level: considering the average number of allocated bits per frame, a target bit rate is fixed for the current frame. For B-frames, the bit allocation can introduce equal, hierarchical or adaptive weights, whereas for I-frames the initial budget is refined using a predefined multiplication weight. Then, the R-λ model is used to compute the frame QP.
-
(iii) CTU level: the process is divided into three main parts. First, the required number of allocated bits for the CTU is computed using the frame budget, the cost of the coded CTUs of the frame and the complexity of the CTUs. The complexity is measured using the MAD [Reference Li, Li, Li and Zhang10] or the sum of absolute transformed differences (SATD) [Reference Karczewicz and Wang12]. Second, the budget is used in the R-λ model to compute λ and then the QP of each CTU. The QP variation is clipped in a pre-defined range. Finally, the last step is the RDO in order to find the optimized mode decision [Reference Ma, Gao and Lu29], referring to the obtained QP. The unit is then repartitioned, coded and all the parameters are updated.
2. COMPARISON BETWEEN THE R-λ MODEL AND QUADRATIC MODEL IN HEVC
Both quadratic and R-λ models have been used for rate control in HEVC. The first proposed controller is based on the unified quadratic model (URQ) described in (4) and has been introduced in HM.5, and then improved in later versions. It helps to reduce bit fluctuation and ensures a good quality encoding [Reference Choi, Nam, Yoo and Sim8]. The R-λ model as represented in (5) has been introduced in HM.11 [Reference Li, Li, Li and Zhang10] and improved in HM.13 [Reference Li, Li and Li11].
Comparative tests made to choose the appropriate model for our work show that global R-D performances are improved using the R-λ model. Referring to Fig. 2 the gain goes from −22.6 to −79.6% for Class E sequences [Reference Bossen30] and using a low delay configuration with an intra period equal to 60.
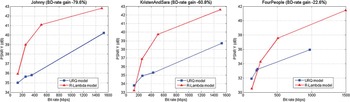
Fig. 2. R–D performances of the R-λ algorithm, compared URQ model.
Fig. 3 shows some per-frame bit cost comparing the used R-λ model and the old URQ model. For example, for the test sequence “Johnny” at different bit rates, R-λ model gives a better bit distribution over GOPs and a smoother repartition of the bit budget at the frame level.

Fig. 3. Comparison of bit fluctuation per frame of R-λ and URQ models for sequence Johnny.
B) GOP-level bit allocation
At the GOP level, bit allocation is performed as described in [Reference Li, Li, Li and Zhang10], taking into account the target bit rate R max , the frame rate f and the number of frames in a GOP N g . The target number of bits in a GOP are determined by:
where the smoothing window S w is equal to 40, N′ s is the number of pictures already coded and T′ s is the bit cost of these pictures.
C) Frame-level bit allocation
Both inter and intra picture bit allocation are supported in the HEVC rate control algorithm, but the process is different. All I-frames belongs to the same level. Thus, the same factor is used to refine their allocated budget, while the cost of inter pictures is determined according to different weights w p for the different hierarchical levels.
At the frame level, an initial budget is allocated per frame, using T g computed in (6) and the bit cost of already coded pictures in the current GOP T′ g ,
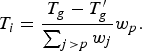 $$T_{i} = \displaystyle{T_{g} - T^{\prime}_{g}\over{\sum_{j \gt p} w_j}} w_{p}.$$
$$T_{i} = \displaystyle{T_{g} - T^{\prime}_{g}\over{\sum_{j \gt p} w_j}} w_{p}.$$
1. WEIGHTED BIT ALLOCATION FOR INTER PICTURES
As said before, at the frame level, three main ways of bit allocation are possible. Equal and hierarchical bit allocations have been introduced in HM.10. Then, adaptive bit allocation has been added in the latest version of HEVC test model (HM.13) [Reference Li, Li and Li11] to improve the model performance. Equal bit allocation method considers the same weight for all B-frames of the sequence. Hierarchical bit allocation consists in giving a predetermined weight to each frame B referring to its level in the GOP and the target bit rate. Using adaptive bit allocation importance weights are updated for each GOP considering the Lagrangian parameter λ computed as in (5) [Reference Li, Li and Li11].
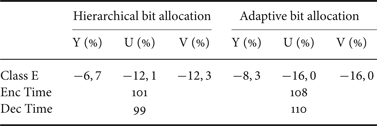
In Table 1, we compare the global performance of the controller using equal, hierarchical and adaptive bit allocation. We compute the R-D performance of the hierarchical method then the adaptive one compared to equal bit allocation. The comparison is made with low delay configuration and using test sequences of class E with video conference content [Reference Bossen30]. Results show that hierarchical and adaptive methods are slightly better then the equal bit allocation and the adaptive allocation gives the best performance, with 1.6% of gain compared to the hierarchical one.
Table 1. R-D performance of R-λ algorithm using hierarchical and adaptive bit allocation, compared to equal bit allocation.
2. BUDGET REFINEMENT FOR INTRA PICTURES
In the R-λ controller implemented in HM.10, the refinement is done considering a weight W that depends on the number of bits per pixel as specified in Table 2 [Reference Li, Li, Li and Zhang10].
Table 2. Intra bit allocation refinement weights.

The final allocated budget per picture T p is then:
where T i is the initial allocated budget. In HM.13, intra picture bit allocation has been improved by replacing the old refinement method by:
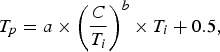 $$T_{p} = a \times \left(\displaystyle{C}\over{T_i}\right)^b \times T_i + 0.5\comma \;$$
$$T_{p} = a \times \left(\displaystyle{C}\over{T_i}\right)^b \times T_i + 0.5\comma \;$$
where a = 0.25, b = 0.5582 and C is the complexity measure of the frame as defined in the next subsection [31].
D) CTU-level bit allocation
Large coding units (LCUs) or CTUs are the basic processing units used in HEVC standard to specify the decoding process. They are basically the replacement of macroblocks and blocks in prior standards. Each unit contains luma coding tree block (CTB) and the corresponding chroma CTBs and syntax elements. Bit allocation at the CTU level depends on three main features: CTU size, complexity measure, and R-λ model.
1. CTU SIZE
The size of a CTU can go up to 64 × 64 pixels in HEVC. At the unit level, rate control algorithm is applied to evaluate the average bit budget for each CTU and then compute a QP from the model. In our work, we consider CTUs of 64 × 64 pixels. First, larger sizes enable better encoding performances. Second, from our tests, the rate control algorithm shows a better matching of the target bitrate when the unit size is equal to 64 × 64.
2. COMPLEXITY MEASURE
To perform bit allocation, a weight w B is computed for each CTU. In HM.10, the weight is estimated by the prediction error (in form of MAD) between the current unit p and the coded unit p′ in the previous coded picture belonging to the same level [Reference Li, Li, Li and Zhang10]. The weight of each CU of index i is defined as:
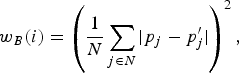 $$w_{B}\lpar i\rpar = \left(\displaystyle{{1}\over{N}} \sum_{j \in N}{\vert p_j - p_j^{\prime}\vert}\right)^2\comma \;$$
$$w_{B}\lpar i\rpar = \left(\displaystyle{{1}\over{N}} \sum_{j \in N}{\vert p_j - p_j^{\prime}\vert}\right)^2\comma \;$$
where N is the number of pixels of the CTU.
In the latest version of the reference software (HM.13) [31], the CTUs weight for B-frames has been modified. It depends on the model parameters α i and β i at the CTU level, the λ of the picture and the number of pixels N. For a CTU of index i:
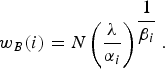 $$w_{B}\lpar i\rpar = N\left(\displaystyle{{\lambda}\over{\alpha_i}}\right)^{\displaystyle{{1}\over{\beta_i}}}.$$
$$w_{B}\lpar i\rpar = N\left(\displaystyle{{\lambda}\over{\alpha_i}}\right)^{\displaystyle{{1}\over{\beta_i}}}.$$
Finally, the complexity measure for I-frame (CTU) is calculated by deriving the sum of absolute Hadamard transformed difference (SATD) as described in [Reference Karczewicz and Wang12]:
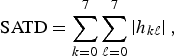 $${\rm SATD}= \sum_{k=0}^{7} \sum_{\ell=0}^{7} \left\vert h_{k\ell}\right\vert \comma \;$$
$${\rm SATD}= \sum_{k=0}^{7} \sum_{\ell=0}^{7} \left\vert h_{k\ell}\right\vert \comma \;$$
where h kl are the coefficients obtained after applying the Hadamard transform to the original 8 × 8 block. The weight w I (i) of a CU of index i is defined as the sum of SATD calculated for all 8 × 8 blocks within the CTU (N b is the number of 8 × 8 units in the CTU).
 $$w_{I}\lpar i\rpar = \sum_{j=0}^{N_b - 1} {\rm SATD}\lpar j\rpar .$$
$$w_{I}\lpar i\rpar = \sum_{j=0}^{N_b - 1} {\rm SATD}\lpar j\rpar .$$
3. R-λ MODEL
The R-λ implementation introduced in HEVC reference software uses different methods of QP computing and bit allocation for the I and the B frames. In HM.10, bit allocation at the CTU level for intra frames was not considered. All the units have the same QP obtained at the frame level. For B-frames, the model introduced by (5) in Section II is used at the CTU level and its parameters α and β are updated after encoding each unit.
In HM.13, to better control the rate allocation of intra coded frames, the complexity measure defined in (12) and (13) is additionally taken into consideration in the R-λ model as follows:
 $$\lambda_i = \alpha \left(\displaystyle{w_I \lpar i\rpar \over R_i}\right)^{\beta}.$$
$$\lambda_i = \alpha \left(\displaystyle{w_I \lpar i\rpar \over R_i}\right)^{\beta}.$$
For a CTU of index i, λ i depends on model parameters at the frame level. The parameters α and β remain constant for the entire frame; however, the number of allocated bits per pixel R i is computed per CTU. Consequently, the model gives a λ and thus a QP for each CTU.
IV. PROPOSED APPROACH
The proposed approach is based on the R-λ model for HEVC. The relationship between R and λ represented by (5) in Section II is used to compute QP of the frame and each CTU of the image. This model has given better performance than the quadratic one [Reference Choi, Nam, Yoo and Sim8, Reference Choi, Nam, Yoo and Sim9].
Our contribution proposes an ROI-based rate control algorithm where the CUs bit allocation depends on the number of bits allocated per region and on the weights of CTUs of the same region. The same process is done independently for units of different regions (ROI or non-ROI). In this section, we describe the initial proposed approach that has been implemented in HM.10 and how we adapted it to the latest version of HEVC test model 13 (HM.13). We focus on the two main steps of the rate control: the bit allocation at both the frame and CTU levels and the computation of QP by the proposed model for both I and B frames.
This section ends up with a detailed description of the adopted ROI-based controller [Reference Chiang, Hsieh, Chang, Jou and Lie4] to HEVC URQ algorithm [Reference Choi, Nam, Yoo and Sim9]. The implementation is done in HM.9 and results are illustrated in the next section.
A) ROI-based model scheme
Fig. 4 shows the proposed ROI-based rate control scheme. The first step consists in detecting the faces in the scene and generating automatically a binary ROI map per frame, which will be given as input to our controller. The target bit rates allocated for the GOP and the current frame are obtained using the reference algorithm described in [Reference Li, Li, Li and Zhang10] and improved in [Reference Karczewicz and Wang12].
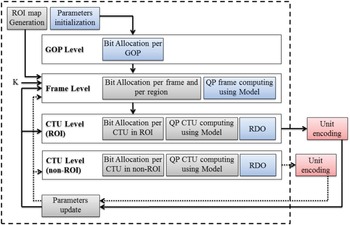
Fig. 4. ROI-based rate control scheme for HEVC.
Then, the frame budget is divided into two parts according to a fixed factor K which is the desired ratio between the bit rate of the ROI and the bit rate of the rest of the frame (non-ROI). At the CTU level, the binary ROI map is used to make a separate bit allocation for CTUs of different regions. The R-λ model is then applied for each CTU using the allocated bit budget for the corresponding region (ROI or non-ROI). Once the CTU is encoded, the model parameters of the corresponding region are updated, and the next CTU is processed in a similar way.
In the first implementation of the controller (in HM.10), the described process is only used for B-frames of different hierarchical levels. Then, it was adapted to HM.13 and introduced in both I-frames and B-frames, considering some differences in complexity computing and model parameters update.
B) Region bit allocation for B-frames
We introduce the region bit allocation at two levels: at the frame level to initialize a target amount of bits for each region, and at the CTU level to make independent bit allocation of CTUs of different regions. At the frame level, the positive constant K is selected. It represents the desired ratio between the ROI and non-ROI bit rates:
where the subscript r denotes the ROI and n the non-ROI. We assume that the current number of allocated bits per frame T p is the sum of the number of bits of the two regions, T r for the ROI and T n for the non-ROI:
where M is the total number of pixels of the frame and P n the area of non-ROI. From (15), (16) and (17), the non-ROI bit rate R n is computed as follows:
At the CTU level, the bit allocation for B-frames depends on the number of bits allocated per region and on the weights of CTUs of the same region. For CTU of index i of the ROI, the allocated bits are:
where T′ r is the effective number of bits of already encoded CTUs of the ROI, I r is the set of indexes of ROI CTU that have not yet been coded, and w r (i) is the weight of the current CTU of the ROI computed referring to (10). The same process is applied independently to CTUs of the rest of the frame (non-ROI).
C) Region-independent rate control models
For B-frames, once the rate of each CTU is found, the QP is computed using the R-λ model. Our proposal separates the models of the different regions. Consequently, the model parameters of CTUs from the ROI r are independent from the ones of CTUs of the non-ROI n. In fact, we have two models; in ROI, using the effective number of bits per pixel R r (i) of each unit of index i ∈ I r ,
and for CTUs from the non-ROI (of index j ∈ I n ), using the effective number of bits per pixel R n (i),
The model parameters are then updated separately. For the ROI, the parameters α r and β r are updated referring to the original rate control algorithm [Reference Li, Li, Li and Zhang10], as follows:
where α′, β′, and λ′ are the updated values of α, β, and λ. In (22) and (24), R′ r is the effective number of bits per pixel after encoding the unit. The same update process is used for the CTUs of the non-ROI.
D) QP and λ variation
The last modification compared to the reference algorithm consists in considering new clipping ranges for λ and QP, at the CTU level. As we try to make independent QP computing for each region, the QP of the current CTU depends on the QP of the last CTU of the same region and the QP of the current frame. We allow a larger QP range than in the reference algorithm, to accommodate differences in quality between the ROI and the non-ROI. We define Δ QP p > 2 and Δ QP u > 1 that guarantees
where QP u , QP p , and QP u′ are respectively the QPs of the current CTU, the current picture and the previously encoded CTU of the same region. It is also possible to consider different clipping ranges for CTUs of different regions and use asymmetric clipping.
E) Extended version of ROI-based rate control algorithm
Modifications have been introduced to our initial approach taking into consideration the evolution of the controller in the new version of HEVC test model (HM.13). There are two main modifications in the new proposal: ROI bit allocation for frame B is adapted to the new version and ROI bit allocation for frame I at the CTU level is introduced.
1. B-FRAMES ROI BIT ALLOCATION
In the new version of the controller, the weight of a CTU is computed by (11). Thus, in our updated ROI-based controller the weight of a CTU from the ROI of index i is expressed as follows:
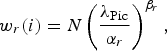 $$w_r\lpar i\rpar = N \left(\displaystyle{\lambda_{\rm Pic}\over \alpha_r}\right)^{\beta_r}\comma \;$$
$$w_r\lpar i\rpar = N \left(\displaystyle{\lambda_{\rm Pic}\over \alpha_r}\right)^{\beta_r}\comma \;$$
where α r and β r are the R-λ model parameters for CTUs of the ROI and λ Pic is the current picture λ. This weight is then used to compute an initial target allocated bit rate T r (i):
The target allocated bits for a CTU
![]() $\widetilde{T}_{r}\lpar i\rpar $
takes into account T
r
(i), the allocated budget for the rest of CTUs of the same region, the effective number of bits of already encoded units of the ROI T′
r
and a smoothing window W fixed at 4 in our simulations:
$\widetilde{T}_{r}\lpar i\rpar $
takes into account T
r
(i), the allocated budget for the rest of CTUs of the same region, the effective number of bits of already encoded units of the ROI T′
r
and a smoothing window W fixed at 4 in our simulations:
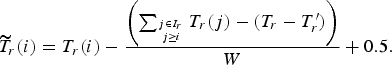 $$\widetilde{T}_{r}\lpar i\rpar = T_r \lpar i\rpar - \displaystyle{{\left(\sum_{j \in I_{r} \atop j \geq i}{T_r\lpar j\rpar } - \lpar T_r - T^{\prime}_r\rpar \right)}\over{W}} + 0.5.$$
$$\widetilde{T}_{r}\lpar i\rpar = T_r \lpar i\rpar - \displaystyle{{\left(\sum_{j \in I_{r} \atop j \geq i}{T_r\lpar j\rpar } - \lpar T_r - T^{\prime}_r\rpar \right)}\over{W}} + 0.5.$$
The number of bits per pixel for a CTU of the ROI is then:
2. I-FRAMES ROI BIT ALLOCATION
At the frame level, the refinement of the initial number of bits is done referring to (9) then the K factor is considered to make ROI-based budget repartition as represented in (29) and compute T
r
and T
n
. At the CTU level, the weight of a unit is its cost and is calculated by deriving the SATD as described in Section III by (12) and (13). This weight is used to compute an initial target allocated bits T
r
(i) as in (28). Then, the number of bits left to encode the ith CTU
![]() $\widetilde{T}_{r}\lpar i\rpar $
is defined as:
$\widetilde{T}_{r}\lpar i\rpar $
is defined as:
 $$\widetilde{T}_{r}\lpar i\rpar =\lpar T_r - T^{\prime}_r\rpar + \displaystyle{{\left(\lpar T_r - T^{\prime}_r\rpar - \sum_{j \in I_{r} \atop j \geq i} T_r \lpar j\rpar \right)\lpar L_r - i\rpar } \over {W}}.$$
$$\widetilde{T}_{r}\lpar i\rpar =\lpar T_r - T^{\prime}_r\rpar + \displaystyle{{\left(\lpar T_r - T^{\prime}_r\rpar - \sum_{j \in I_{r} \atop j \geq i} T_r \lpar j\rpar \right)\lpar L_r - i\rpar } \over {W}}.$$
Finally, the number of bits per pixel for an intra CTU of the ROI is:
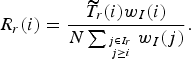 $$R_r \lpar i\rpar = \displaystyle{{\widetilde{T}_{r}\lpar i\rpar w_I\lpar i\rpar }\over{N \sum_{j \in I_{r} \atop j \geq i}{w_I \lpar j\rpar }}}.$$
$$R_r \lpar i\rpar = \displaystyle{{\widetilde{T}_{r}\lpar i\rpar w_I\lpar i\rpar }\over{N \sum_{j \in I_{r} \atop j \geq i}{w_I \lpar j\rpar }}}.$$
F) URQ ROI-based controller for HEVC
This section introduces a second ROI-based controller. As said before, the idea has been proposed in [Reference Chiang, Hsieh, Chang, Jou and Lie4] for H.264 standard and it consists in estimating the bit count per region using a quadratic R-D model. We adopted this algorithm to the URQ controller introduced in [Reference Choi, Nam, Yoo and Sim9]. The final version of the URQ ROI-based algorithm is then based on the model proposed in [Reference Chiang, Hsieh, Chang, Jou and Lie4] and the controller implemented in HM.9 [32], but enhanced with several features.
1. BIT ALLOCATION PER REGION
At the frame level, separate bit allocation per region is performed. First, the initial budget fixed by the network is divided into two parts using a quality factor K as defined in (15) assigned by users or control systems. Target bit counts T r and T n are initialized to ROI and non-ROI referring to (16), then used for bit allocation at the frame and CTU levels.
The final target bit left budget
![]() $\widehat{T}_{r}\lpar i\rpar $
for CTU from the ROI is based on the remaining bits in ROI (T
r
− T′
r
), the number of pixels in the current CTU N(i) and the number of pixels left in ROI:
$\widehat{T}_{r}\lpar i\rpar $
for CTU from the ROI is based on the remaining bits in ROI (T
r
− T′
r
), the number of pixels in the current CTU N(i) and the number of pixels left in ROI:
 $$\widehat{T}_{r}\lpar i\rpar = \displaystyle{{\lpar T_r - T^{\prime}_r\rpar \times N\lpar i\rpar }\over{\sum_{j \in I_{r} \atop j \gt i} N\lpar j\rpar }}.$$
$$\widehat{T}_{r}\lpar i\rpar = \displaystyle{{\lpar T_r - T^{\prime}_r\rpar \times N\lpar i\rpar }\over{\sum_{j \in I_{r} \atop j \gt i} N\lpar j\rpar }}.$$
The final target bit occupancy
![]() $\widetilde{T}_{r}\lpar i\rpar $
for CTU from the ROI is computed using the initialized bit count in ROI and ROI virtual buffer occupancy V
r
(i):
$\widetilde{T}_{r}\lpar i\rpar $
for CTU from the ROI is computed using the initialized bit count in ROI and ROI virtual buffer occupancy V
r
(i):
where U r (i) is the number of units left in ROI after encoding CTU of index i.
The final bit budget is a weighted average of the target bit left and the target bit occupancy:
where β is the weight defined in [Reference Choi, Nam, Yoo and Sim9]. The same process is done for CTUs of the rest of the frame.
2. URQ MODEL FOR QP DETERMINATION
The strategy for intra pictures and non-reference frames is kept as described in the document [Reference Choi, Nam, Yoo and Sim9] while the ROI-based URQ model is used at the CTU level for referenced B-frames. In this case, the final bit target T r f is refined as follows:
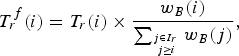 $$T^f_r\lpar i\rpar = T_r\lpar i\rpar \times \displaystyle{{w_B\lpar i\rpar }\over{\sum_{j \in I_{r} \atop j \geq i} w_B\lpar j\rpar }}\comma \;$$
$$T^f_r\lpar i\rpar = T_r\lpar i\rpar \times \displaystyle{{w_B\lpar i\rpar }\over{\sum_{j \in I_{r} \atop j \geq i} w_B\lpar j\rpar }}\comma \;$$
where w B (i) is the MAD of the current CTU as expressed in (10). After estimating this target bit count for the considered CTU, the preliminary QP value is determined as in [Reference Choi, Nam, Yoo and Sim9] by the quadratic model introduced in (4).
3. QP ADJUSTMENT
The QP obtained using the quadratic R-D model is then modified by considering the smoothness issues over the temporal and spatial domains. The four constraints proposed in [Reference Chiang, Hsieh, Chang, Jou and Lie4] are used. All QPs are then clipped between 0 and 51 as proposed in URQ reference controller implemented in HM.9.
V. EXPERIMENTAL RESULTS
A) Test conditions
First, we implemented the proposed rate control scheme on HEVC test model 10 (HM.10) [33] and we evaluated the obtained results. Then we introduced the extended version on HM.13 [31, Reference Kim, McCann, Sugimoto, Bross, Han and Sullivan34] by taking into account the evolution of the controller and compared the obtained results in the two cases. Finally, we implemented the URQ ROI-based model in HM.9 [32]. Performed tests help us evaluate and compare the performance of the proposed methods.
To compute a binary map as represented in Fig. 5, we used the same ROI detection method. We introduce HM Viola and Jones object detection algorithm [Reference Viola and Jones16].

Fig. 5. Test sequences and ROI maps (a) Johnny (ROI represents 13%), (b) KristenAndSara (ROI represents 14%), (c) FourPeople (ROI represents 10%).
Since video conferencing applications require low coding delay, all pictures were coded in display order. Three different configurations have been used to test the first and the second ROI-based controller: All-B, All-I, and an hybrid configuration that considers GOPs of B-frames and introduces an intra picture each second. In the first and the third algorithms (HM.10 and HM.9), I-frame bit allocation at the CTU level has not been yet introduced, so, all the frames were considered as B-frames except the first one (I-frame), while, for the extended version of our code in HM.13, we tested all the configurations.
Three HD 720p sequences from class E have been tested: “Johnny”, “KristenAndSara”, “FourPeople” [Reference Bossen30]. As we can see in Fig. 5, the selected test sequences have typical video conferencing content and different characteristics, like number of faces and ROI size. We used different bit rates, budget partitioning per-region and QP ranges to evaluate the performance of our approach.
B) Implementation and performed tests
The introduced modifications have been done mainly in rate control class of the reference softwares HM.10 [33], HM.13 [31], and HM.9 [32]. A reference test “Ref” is performed using the rate control algorithm described in [Reference Li, Li, Li and Zhang10] and improved in [Reference Li, Li and Li11]. While evaluating the URQ model the reference used is described in [Reference Choi, Nam, Yoo and Sim9]. These first tests give us the reference performance: the ratio K between ROI bit rate and non-ROI bit rate, the bit budget used for encoding each region, the PSNR and the structural similarity (SSIM) index [Reference Zhao, Zeng, Rehman and Wang35] of each region that goes from 0 to 100. Second, we activate all modified functions: we introduce a new bit repartitioning between regions by fixing a factor K and a large QP margin. Then we perform an evaluation test of our method that we note “New”.
C) Performance of ROI-based controller in HM.10
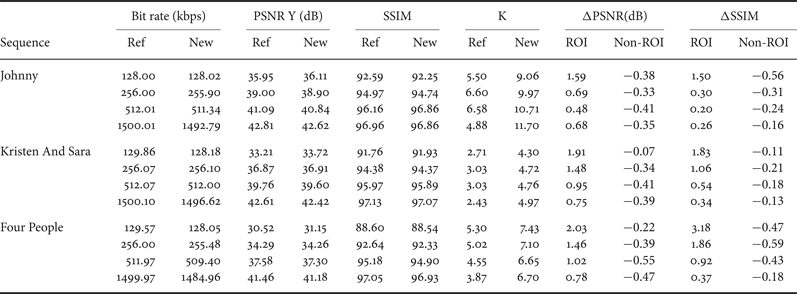
Table 3 summarizes the results of the performed test at 128 and 256 kbps. Both equal and hierarchical bit allocations are tested. The table shows that introducing a K factor for bit repartitioning between regions does not impair the R-D performance. We can increase the effective ratio comparing to the reference by keeping an output bit rate close to the assigned value. Moreover, the overall PSNR is practically the same as the reference encoder.
Table 3. Control accuracy comparison of the reference and the proposed controller for inter frames using HM.10.
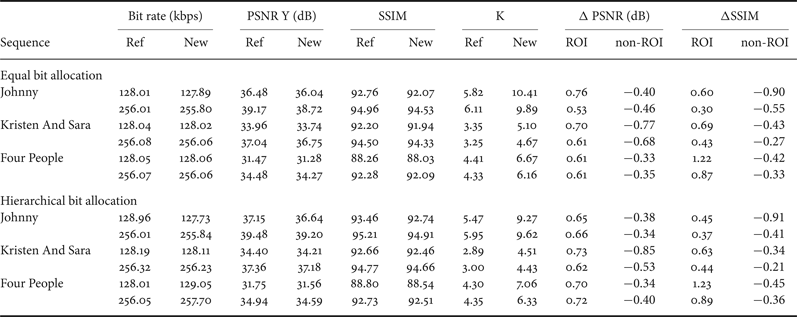
Table 4. Control accuracy comparison of the reference and the proposed controller for intra frames using HM.13.
Now we examine the quality of ROI and non-ROI for different ratios K. In Table 3, ΔPSNR ROI is the difference in quality of the ROI using the proposed controller and the reference one and ΔSSIM ROI is the difference in similarity of the ROI using the proposed controller and the reference one (and the same for non-ROI). We notice that the overall quality of the ROIs is improved using different configurations but also different target rates. The global gain in the ROI goes from 0.5 to 0.7 dB in terms of PSNR and from 0.3 to 1.2 in terms of SSIM. However, as we reduce the number of allocated bits in the non-ROI, its quality decreases.
In Fig. 6, we plot ΔPSNR of the ROI and ΔPSNR of the non-ROI per GOP. Overall, the bigger is K the better is the global quality of the ROI in the sequence and the lower is the PSNR of the non-ROI. The quality of the ROI is improved in all the GOPs (and frames) while the quality of the non-ROI is slightly decreased. The curves show that for each region the difference in quality between the proposed scheme and the reference RC [Reference Li, Li, Li and Zhang10] is more important when K is bigger. This means that our method leads to allocate more bits to the ROI by improving its quality and respecting the bit rate constraint.
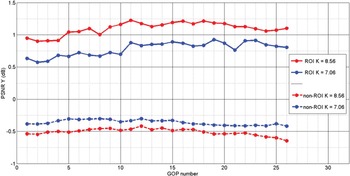
Fig. 6. ΔPSNR ROI and non-ROI (dB) for the last 25 GOPs of FourPeople at 128 kbps and using hierarchical bit allocation.
D) Performance of ROI-based controller in HM.13
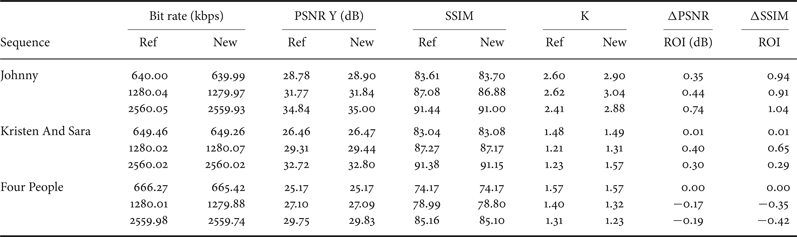
1. INTRA PICTURE ROI-BASED ALGORITHM PERFORMANCE
Using the all intra configuration of the encoder, we tested the performance of the proposed algorithm. Three different rate points are used per sequence (640, 1280, and 2560 kbps). The budget constraint is respected and the global quality is not altered.
In intra case, units from the ROI are coded from other units of the non-ROI. Consequently, our novel bit repartition affects the non-ROI and so the ROI. We can see that in some cases the quality of the ROI decreases.
2. INTER PICTURE ROI-BASED ALGORITHM PERFORMANCE
A low delay B configuration is used to evaluate the performance of ROI-based allocation for B-frames. We first evaluate the global performance as done in HM.10. Results are given at 128 and 256 kbps to compare the performance with the first version of the controller. Equal, hierarchical, and adaptive bit allocations are tested.
From Table 5 we can deduce the same conclusions as in the previous version of our controller implemented in HM.10: the bit budget constraint is respected and ROI quality is improved proportionally to the repartition factor K.
Table 5. Control accuracy comparison of the reference and the proposed controller for inter frames using HM.13.
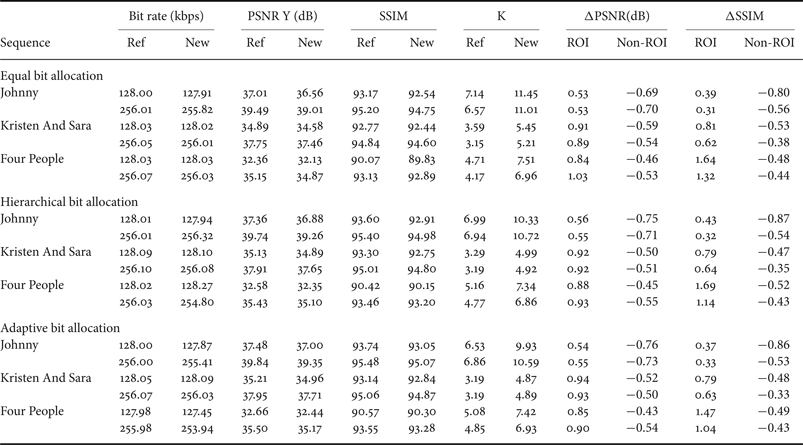
At the CTU level the proposed approach gives a new QP distribution. Fig. 7 shows that smaller QP values are assigned to Johnny's face (QP = 30), while the rest of the frame takes bigger QPs that go from 34 to 38.
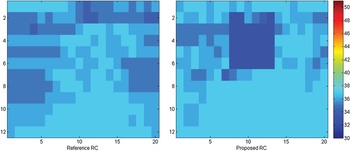
Fig. 7. Comparison of QP repartition at the CTU level of Johnny.
3. ROI-BASED ALGORITHM PERFORMANCE USING HYBRID CONFIGURATION
For a video conferencing system the low delay configuration is the most appropriate as we have the real-time constraint. However, to reduce packet loss effect and limit error propagation, an intra frame is introduced every second. Consequently, the final configuration of our encoder is the hybrid one. It handles a GOP of four B-frames coded in display order and an I-frame after 60 inter pictures. We choose the adaptive bit allocation at the frame level as it gives the best R-D performances and we tested four different rate points per sequence (128, 256, 512, and 1500 kbps).
From Table 6, we conclude that the controller global performance is maintained and the quality of the ROI is improved. At low bit rate, we can gain up to 2 dB in the ROI. Moreover, SSIM of the ROI is improved considerably when picture SSIM is smaller than 95. We can reach an improvement in the ROI quality of 3.18 dB for example. As SSIM is saturated when it gets close to 100, ΔSSIM is reduced when the picture index is higher than 95. We still in that case have noticeable improvement in ROI quality as the SSIM index goes from 0.20 to 0.92.
Table 6. Control accuracy comparison of the reference and the proposed controller in HM.13
Experimental results show advantages in objective PSNR, in SSIM that predicts subjective opinion with high precision and visual evaluation for ROI as represented in Figs 8–13. We notice that for both intra and inter pictures and using our proposed scheme we can distinguish more details in the face and less artifacts, while the non-ROI does not present noticeable deterioration in visual quality as in video conferencing system the background is not changing in most of the cases.

Fig. 8. Subjective comparison of Johnny coded at 128 kbps for an I frame. (a) Reference RC, (b) Proposed RC.
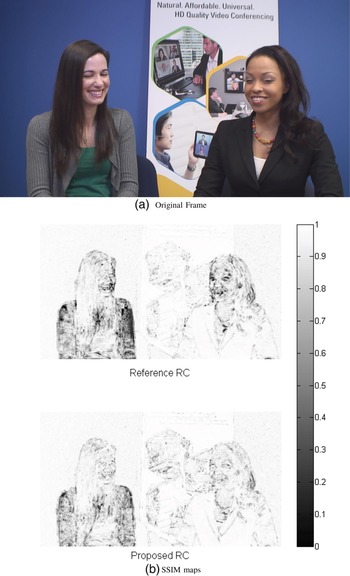
Fig. 9. Subjective comparison of Johnny coded at 128 kbps for a B frame. (a) Reference RC, (b) Proposed RC.

Fig. 10. Subjective comparison of KristenAndSara coded at 128 kbps for an I frame. (a) Reference RC, (b) proposed RC.

Fig. 11. Subjective comparison of KristenAndSara coded at 128 kbps for a B frame. (a) Reference RC, (b) proposed RC.

Fig. 12. Subjective comparison of FourPeople coded at 128 kbps for an I frame. (a) Reference RC, (b) proposed RC.

Fig. 13. Subjective comparison of FourPeople coded at 128 kbps for a B frame. (a) Reference RC, (b) proposed RC.
Locally the SSIM index has been evaluated and an SSIM map has been computed for each frame to prove quality improvement in the ROI. Figs 14–16 represent the SSIM index over the whole frames (SSIM values goes from 0 for high distortion to 1 for high similarity). We notice that considering the proposed method SSIM index in the faces is closer to 1 (white faces). It shows an improvement in the details of the faces of the three tested sequences.

Fig. 14. SSIM map comparison Johnny. (a) Original frame, (b) SSIM maps.

Fig. 15. SSIM map comparison KristenAndSara (a) Original Frame, (b) SSIM maps.
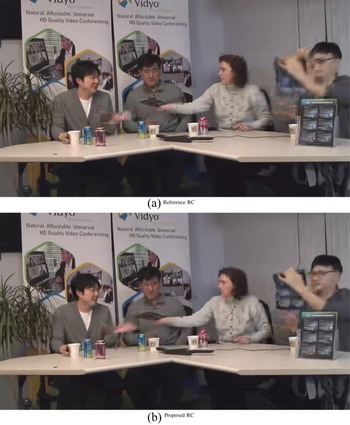
Fig. 16. SSIM map comparison FourPeople. (a) Original frame, (b) SSIM maps.
E) Comparison of the proposed R-λ ROI-based controller with URQ ROI-based controller
The last step consists in using an ROI-based RC algorithm initially proposed for H.264 and based on the quadratic model, then, adapt it to HEVC as described in Section IV. The performed tests in this section use a low delay configuration where all frames are coded in bidirectional mode (B-frames). We tested the three sequences at four different bit rates (128, 256, 512, and 1500 kbps).
We notice from Table 7 that the URQ ROI-based method implemented in HM.9 respects the budget constraint at low bit rate. It is also the case at high bit rate as represented in Fig. 17.

Fig. 17. R-D performances of R-λ ROI-based algorithm and URQ ROI-based model compared to URQ reference RC algorithm.
Table 7. RC results using URQ model at 128 kbps.
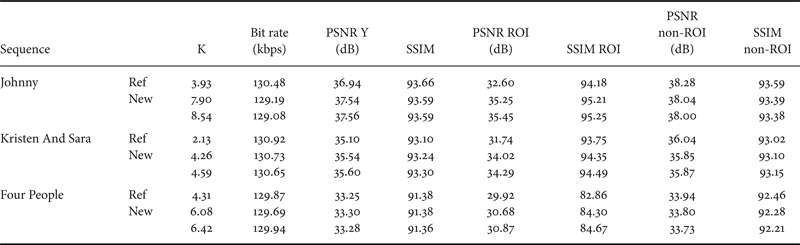
R–D performance evaluation shows an important improvement in rate control performances. The obtained R-D curve is better than the reference URQ model and comparable to the one given by our R-λ algorithm implemented in HM.13. Moreover, table 7 shows that URQ ROI-based method improves the quality of the ROI while using higher bit ratio K.
Fig. 18 shows bit distribution over GOP at low and high bit rates for Johnny sequence. We conclude that the proposed R-λ method gives a smoother bit allocation compared to the URQ methods at low bit rate with no unsettled bit picks, while at high bit rate the three algorithms gives comparable distribution over GOPs. The same conclusion is valid for all tested sequences.
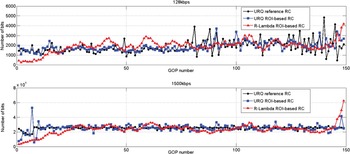
Fig. 18. Comparison of bit fluctuation per GOP of R-λ and URQ ROI-based models at low and high bit rate for sequence Johnny.
Fig. 19 represents R-D performance of all evaluated methods. It gives the overall ROI PSNR for each bit rate. For the three tested sequences, the reference URQ controller has the worst R–D performances. Once introducing the ROI, both URQ-based method and R-λ-based method show better R-D performance compared with the reference.
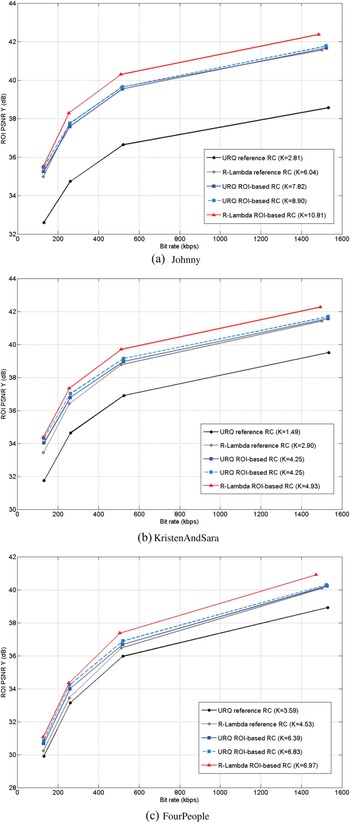
Fig. 19. Comparative ROI-based R-D performances of different methods. (a) Johnny, (b) KristenAndSara, and (c) FourPeople.
Finally, in the URQ scheme ROI-based bit allocation is only performed for referenced frames of type B. Our algorithm (based on R-λ method) makes ROI-based allocation for all frame types, which leads to a better QP repartition over regions in the full sequence. With our algorithm we can reach higher ratios K, as shown in Fig. 19.
VI. CONCLUSION
In this paper, an ROI-based rate control for HEVC is proposed for HM.10 and improved for HM.13. A second ROI-based RC algorithm studied in the state-of-the-art has been adapted to HEVC controller and implemented in HM.9.
Our proposed scheme uses the R-λ model, takes into account both I and B frames and achieves better visual quality in ROIs thanks to an independent processing of ROI and non-ROI regions at the CTU level and a larger QP clipping range, while the reference scheme used the quadratic model and performs rate control only in referenced B-frames.
The proposed algorithms lead to better quality in ROI, while respecting the global bit rate constraint. All implemented schemes are useful for video conferencing systems to allow a better representation of the facial expression.
Marwa Meddeb (S′13) received the double engineering degree in telecommunications from the High School of Communication of Tunis (SUP'COM), Tunis, Tunisia and Télécom ParisTech, Paris, France, in 2013 thanks to a double degree program in telecommunications and multimedia technologies within EURECOM, Sophia Antipolis, France. Since February 2013, she is working toward the Ph.D. degree within the Image and Signal Processing Department at Télécom ParisTech (Paris, France). Her research interests includes image and video coding, segmentation and transmission.
Marco Cagnazzo (M′05-SM′11) obtained the Laurea (equivalent to the M.S.) degree in Telecommunication Engineering from Federico II University, Napoli, Italy, in 2002, and the Ph.D. degree in Information and Communication Technology from Federico II University and the University of Nice-Sophia Antipolis, Nice, France in 2005.
He was a post-doc fellow at I3S Laboratory (Sophia Antipolis, France) from 2006 to 2008. Since February 2008 he has been Associate Professor at Institut Mines-Télécom, Télécom ParisTech (Paris), within the Multimedia team. He is author of more than 90 contributions in peer-reviewed journals, conferences proceedings, books and book chapters. His current research interests are three-dimensional video communication and coding, distribued video coding, robust video delivery, network coding.
Dr. Cagnazzo is an Area Editor for Elsevier Signal Processing: Image Communication and Elsevier Signal Processing. Moreover he is a reviewer for major international scientific reviews (IEEE Trans. Multimedia, IEEE Trans. Image Processing, IEEE Trans. Signal Processing, IEEE Trans. Circ. Syst. Video Tech., Elsevier Signal Processing, Elsevier Sig. Proc. Image Comm., and others) and conferences (IEEE International Conference on Image Processing, IEEE MMSP, European Signal Processing Conference, and others).
Béatrice Pesquet-Popescu (SM′06, F′13) received the engineering degree in telecommunications from the “Politehnica” Institute in Bucharest in 1995 (highest honours) and the Ph.D. degree from the Ecole Normale Supérieure de Cachan in 1998. In 1998, she was a Research and Teaching Assistant with Université Paris XI, Paris. In 1999, she joined Philips Research France, Suresnes, France, where she worked for two years as a Research Scientist, then as a Project Leader, in scalable video coding. Since Oct. 2000 she is with Télécom ParisTech (formerly, ENST), first as an Associate Professor, and since 2007 as a Professor, Head of the Multimedia Group. She is the Head of the UBIMEDIA common research laboratory between Alcatel-Lucent and Institut Télécom. Her current research interests are in source coding, scalable, robust and distributed video compression and sparse representations. Dr. Pesquet-Popescu was an EURASIP BoG member (2003–2010), and an IEEE Signal Processing Society IVMSP TC member and MMSP TC associate member. She serves as an Associate Editor for IEEE Trans. on Image Processing, IEEE Trans. on Multimedia, IEEE Trans. on CSVT, Elsevier Image Communication, and Hindawi Int. J. Digital Multimedia Broadcasting journals and was till 2010 an Associate Editor for Elsevier Signal Processing. She was a Technical Co-Chair for the PCS2004 conference, and General Co-Chair for IEEE SPS MMSP2010, EUSIPCO 2012, and IEEE SPS ICIP 2014 conferences. Beatrice Pesquet-Popescu is a recipient of the “Best Student Paper Award” in the IEEE Signal Processing Workshop on Higher-Order Statistics in 1997, of the Bronze Inventor Medal from Philips Research and in 1998 she received a “Young Investigator Award” granted by the French Physical Society. She holds 23 patents in wavelet-based video coding and has authored more than 290 book chapters, journal and conference papers in the field. In 2006, she was the recipient, together with D. Turaga and M. van der Schaar, of the IEEE Trans. on Circuits and Systems for Video Technology “Best Paper Award”.



























