I. INTRODUCTION
Nowadays, the demand continues to increase for speaker recognition technology in such applications as telephony, security, and communication. For example, the application of voice mining is used to monitor the communications, which is popularly adopted by intelligence agencies, government and law Enforcement. Speaker recognition is a kind of biometric verification such as fingerprint, iris, and face recognition. The major components of speaker recognition, which finds the identity information of a speaker from speech signals, include feature analysis, statistical modeling, and verification decision.
Most speaker recognition systems use cepstrum-based features such as Mel-frequency cepstral coefficients (MFCC) [Reference Davis and Mermelstein1] or perceptual linear prediction [Reference Hermansky2] cepstral coefficients, which provide an estimate of short-term energy as a function of frequency. Gaussian mixture model (GMM) has been commonly applied for statistical modeling in speaker recognition applications with speaker adaptation techniques. To solve speaker data sparseness and channel mismatch problems, maximum a posteriori (MAP) has been widely used to adapt the speaker model from the universal background model (UBM) [Reference Bimbot3]. To compensate the channel and session effects, eigenchannel is applied in speaker recognition [Reference Kenny, Boulianne, Ouellet and Dumouchel4]. Recently, i-vector technique is proposed to estimate total variability for speaker adaptation [Reference Dehak, Kenny, Dehak, Dumouchel and Ouellet5].
Different from speech recognition with HMM modeling [Reference Huang and Wu6], the common speaker recognition methods are based on GMM framework. The advantage of the GMM-based approach is that speaker recognition can be performed in a completely text-independent manner [Reference Park and Hazen7] and all speech frames without any transcription and segmentation are used to estimate speaker information and build GMMs. However, one disadvantage of such a GMM modeling approach is that the acoustic variability of phonetic events is not taken into account during comparisons with different speakers [Reference Park and Hazen7]. To solve this problem, many previous studies focused on using specific constrained groups of data to improve the speaker recognition performance.
A) Related works in ensemble-based speaker recognition
The generalization ability of an ensemble could be significantly better than that of a single learner. Zhang et al. intended to improve the performance of the speaker recognition system by introducing a novel method combining optimizing annular region-weighted distance k-nearest neighbor with BagWithProb ensemble learning schemes [Reference Zhang, Tang, Li and Qian8]. In the DataBoost-UP algorithm, the data (i-vectors) is synthesized using the utterance partitioning technique instead of random generation of attribute values in the minimum and maximum interval. Both the minority (target speaker) and majority (background speakers) classes are oversampled to prevent overemphasis on the hard instances of the minority class. The DataBoost-UP is used to create an ensemble of SVM classifiers [Reference Sreenivasa Rao and Sarkar9]. Sturim et al. presented text-constrained Gaussian mixture models to close the gap between text-dependent and text-independent speaker verification. Speech is segmented into acoustic units such as words or phones, and then GMM–UBM verifiers are trained and tested using only speech from constrained groups of units [Reference Sturim, Reynolds, Dunn and Quatieri10]. Park and Hazen proposed speaker identification using domain-dependent automatic speech recognition (ASR) to provide phonetic segmentation. A combination of classifiers is used to reduce identification errors [Reference Park and Hazen7]. Baker et al. studied GMM modeling using multilingual broad phonetics to construct syllabic events and segmentations for speaker verification [Reference Baker, Vogt and Sridharan11]. Bocklet and Shriberg described a speaker recognition approach using syllable-level constraints for cepstral frame selection. Complementary information and improvement can be found by combining eight subsystems including syllable onsets, syllable nucleii, syllable codas, syllables following pauses, one-syllable words, and three other kinds of syllables [Reference Bocklet and Shriberg12]. Sanchez et al. studied the performances between constraint-dependent and constraint-independent approaches for training UBMs and joint factor analysis. They explored unit-based constraints, which are regions constrained by specific syllables, phones, or sub-phone regions [Reference Sanchez, Ferrer, Shriberg and Stolcke13]. In addition, unsupervised clustering was applied to speaker recognition to compensate the domain mismatch between training, enrollment, and testing data in [Reference Shum, Reynolds, Garcia-Romero and McCree14]. Attempts of ensemble of speaker recognition systems have been made in [Reference Garcia-Romero, Zhou and Espy-Wilson15].
All of the above work segmented and selected data for more detailed speaker model construction based on prosody, syllable, or phoneme analysis. Although these approaches showed improvements in speaker recognition, many shortcomings remain in them. For example, the quality of the feature frame selection is obviously influenced by the accuracy of ASR or prosody estimation systems. Furthermore, prior or auxiliary knowledge is required for such constrain-based approaches as language information. According to these reasons, we do not have experimental comparisons. Although there is no comparison with the existing work on the ensemble of speaker recognition, the performance of the proposed method is consistently better than the baseline.
B) Proposed framework
In this study, we propose an ensemble learning using unsupervised data selection, which considers acoustic variability in the model training, speaker enrollment and testing. The speech data are segmented into several subsets of speech frames without any auxiliary information or pre-processor (ASR or prosody estimator systems) and then ensemble classifiers are trained using these subsets in a divide-and-conquer manner. The ensemble framework is similar to neural networks or mixture of experts [Reference Jacobs, Jordan, Nowlan and Hinton16]. In such a way, we can avoid the local optimization training when a single conventional classifier is adopted.
Figure 1 shows the pipeline of the proposed ensemble-based speaker recognition using unsupervised data selection. Basically, there are three elements before we do ensemble training and testing. First, at the feature extraction stage, we aim at extracting discriminative and effective acoustic features by applying long-term feature (LTF) analysis. Second, at the distance metric stage, we explore two categories of distance metrics, including vector-based and likelihood-based distance metrics, to measure the similarity between data. Finally, the clustering algorithm can be naturally employed at the clustering stage. We conducted experiments on the 2010 and 2008 NIST Speaker Recognition Evaluation (SRE) datasets.

Fig. 1. The pipeline of the proposed ensemble based speaker recognition using unsupervised data selection.
C) Outline of the paper
The rest of this paper is organized as follows. In Sections II–IV, the pipeline of the proposed method, namely, feature extraction, distance metric, and clustering for ensemble-based speaker recognition, are described. In Section V, we describe our experiment setup and protocol, and introduce the performance evaluation metrics. We present the experiment results as well as a discussion of the results in Section VI. Finally, we conclude this work in Section VII.
II. FEATURE EXTRACTION
At the first stage of ensemble-based speaker recognition pipeline is feature extraction. Feature extraction is an important process to estimate a numerical representation from speech samples and to characterize the speakers. Many kinds of feature analysis have been proposed for speaker recognition in previous studies. The conventional short-term spectral features, such as MFCC, are useful acoustic features for speaker recognition. Many efforts have been devoted to improving the effectiveness of MFCC, such as reducing the dimensionality, enhancing discriminative ability [Reference Gales17], and characterizing speakers with temporal features [Reference Reynolds18]. Due to the importance of phase in human speech, features are extracted by integrating MFCC and phase information for speaker identification and verification [Reference Wang, Ohtsuka and Nakagawa19]. In deep neural network (DNN) speech recognition [Reference Pan, Liu, Wang and Hu20], experiments show the gain of DNN is almost entirely attributed to DNN's feature vectors that are concatenated from several consecutive speech frames within a relatively long context window. In this study, we aim at extracting discriminative and effective acoustic features for speaker recognition, by applying LTF analysis to enhance the discriminative capability of short-term spectral features as shown in Fig. 2.

Fig. 2. Illustration of speaker discriminative feature analysis using the mean of short-term spectral features in a long-term window.
We applied LTF analysis [Reference Huang, Su, Ma and Li21] as the feature extraction based on the traditional MFCCs of a short-time spectral analysis of 16 ms. We extracted 36 MFCCs consisting of 12 coefficients in addition to the first and second derivatives. Speech signals were divided into 18 sub-bands between 250 and 3500 Hz using the Mel-filter bank to make spectral contents that resemble those of telephone channels. LTF is used to average several short-time spectral features in a long-time window and capture the spectral statistics over a long period of time. The overlapping long-term windows are applied on the short-term features, reducing short-term MFCC frames J to LTF frames K, with K=(J−L)/Z+1. L denotes the size of the long-term window and Z is the step of the long-term window shift. Since the mean of multiple short-term spectral features is used, LTF can simultaneously take account of short-term frequency characteristics and long-term resolution. This transformation results in a more compact feature vector for statistical modeling. According to the previous study [Reference Huang, Su, Ma and Li21], the optimal values of L and Z were 4 and 2, respectively.
III. DISTANCE METRIC
The second stage of ensemble-based speaker recognition pipeline is distance metric calculation. The distance metric calculation of ensemble-based speaker recognition is similar to the speaker diarization scheme [Reference Anguera Miro, Bozonnet, Evans, Fredouille, Friedland and Vinyals22,Reference Senoussaoui, Montreìal, Kenny, Stafylakis and Dumouchel23]. The similarity of between them is to search for homogeneous segments. The differences between them are purposes. In speaker diarization, speaker segmentation is applied to extract the longest possible homogenous segments in a conversation. In ensemble-based speaker recognition, the distance metric calculation is used to measure similarity of short feature frames in speech of a speaker. The distance metrics are used for acoustic clustering of the speech data. We explore two distance metrics, the vector-based and likelihood-based distance metrics, to measure the similarity and construct partitioning clusters for ensemble learning.
A) Vector-based distance metrics
In this study, we use the LTF to analysis acoustic characteristics on the longer range. A feature frame can be viewed as a data point in an n-dimensional vector space. The data points with similar acoustic characteristics tend to cluster together. Thus, Euclidean and Mahalanobis distance metrics are reasonable solutions for the clustering. We applied Euclidean distance to measure the length of the path connecting two feature vectors. The Euclidean distance between vectors x and y in an n-dimensional space is given by
The other common distance measure is the Mahalanobis distance metric. The Mahalanobis distance metric considers correlations of data, and thus the similarity is estimated by
where A is the covariance matrix. In addition, the cosine measure is a type of vector-based distance metric used to estimate the similarity between vectors x and y as
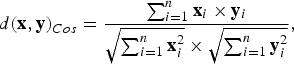 $$d{(\bf{x},\bf{y})}_{Cos} ={{\sum\nolimits_{i=1}^n {\bf{x}}_i \times {\bf{y}}_{i} }\over{\sqrt {\sum\nolimits_{i=1}^n {\bf{x}}_{i}^2 } \times \sqrt{\sum\nolimits_{i=1}^n {\bf{y}}_{i}^2}}}, $$
$$d{(\bf{x},\bf{y})}_{Cos} ={{\sum\nolimits_{i=1}^n {\bf{x}}_i \times {\bf{y}}_{i} }\over{\sqrt {\sum\nolimits_{i=1}^n {\bf{x}}_{i}^2 } \times \sqrt{\sum\nolimits_{i=1}^n {\bf{y}}_{i}^2}}}, $$
where n is the dimension of the feature vector. The cosine distance is suitable to measure the similarity between the data points with strong directional scattering patterns. For instance, the cosine distance is popularly used on the applications of information retrieval [Reference Huang and Wu24,Reference Huang, Ma, Li and Wu25] and i-vector-based speaker recognition [Reference Dehak, Kenny, Dehak, Dumouchel and Ouellet5].
B) Likelihood-based distance metric
Besides the vector-based distance metrics, we can also use the likelihood estimation for the similarity measure. We explore two likelihood-based similarity measures. One is the log-likelihood distance metric. The other is delta-Bayesian information criterion (BIC) estimation. We treat each cluster as a Gaussian model
![]() $\lambda =\{{\bf{u}},{\bf{\Sigma}}\}$
in the log-likelihood estimation. The log-likelihood score is estimated by
$\lambda =\{{\bf{u}},{\bf{\Sigma}}\}$
in the log-likelihood estimation. The log-likelihood score is estimated by
where
![]() $L(\bf{x}\vert \lambda _{k} )$
is the likelihood of acoustic feature x given the model λ
k
. The mean vector
$L(\bf{x}\vert \lambda _{k} )$
is the likelihood of acoustic feature x given the model λ
k
. The mean vector
![]() $\bf{u}_{k} \in \Re ^{n}$
and the covariance matrix
$\bf{u}_{k} \in \Re ^{n}$
and the covariance matrix
![]() $\bf{\Sigma}_{k} \in \Re ^{n}$
are applied for each Gaussian; n is the dimension of acoustic feature vector x\ and\ k is the label of the cluster.
$\bf{\Sigma}_{k} \in \Re ^{n}$
are applied for each Gaussian; n is the dimension of acoustic feature vector x\ and\ k is the label of the cluster.
The other likelihood-based similarity measurement is the BIC which can be used for speaker clustering [Reference Schwarz26]. The BIC value shows how well the data x fit the model λ k estimated by
where ε is a design parameter, δ k is the number of free parameters in λ k , and n x is the number of feature vectors in x. The similarity between data x and y is given by the delta-BIC score. The delta-BIC score is widely used for audio segmentation, model selection, and speaker clustering [Reference Wu and Hsieh27,Reference Tang, Chu, Hasegawa-Johnson and Huang28]. Based on Gaussian assumption, the delta-BIC score between x and y is estimated by
where N=N
x
+N
y
is the total number of frames.
![]() $\bf{\Sigma}_{x}$
and
$\bf{\Sigma}_{x}$
and
![]() $\bf{\Sigma}_{y}$
represent the covariance matrices of x and y, respectively.
$\bf{\Sigma}_{y}$
represent the covariance matrices of x and y, respectively.
![]() $\bf{\Sigma }$
is the covariance matrix of the aggregate of x and y. P is a penalty factor given by
$\bf{\Sigma }$
is the covariance matrix of the aggregate of x and y. P is a penalty factor given by
with different penalty factors, we can perform various model selection criterions such as AIC and MDL [Reference Wu and Hsieh27].
IV. CLUSTERING FOR ENSEMBLE BASED SPEAKER RECOGNITION SYSTEMS
The last stage of ensemble-based speaker recognition pipeline is clustering. In this study, we investigate two clustering algorithms for the unsupervised data selection and the combination of ensemble classifiers.
A) Unsupervised clustering
The unsupervised data selection can be achieved in various ways. We explore two data clustering algorithms based on the partitioning and hierarchical techniques in this study. One popular partitioning technique is the K-means clustering algorithm that partitions data into K clusters in which each data belongs to the cluster with the nearest mean. The K-means clustering algorithm aims to assign every speech frames in a cluster to its respective acoustic characteristics. For example, we can find that the gender information is identified if we set the number of clusters is two. We implement the K-means clustering algorithm with multiple random starting points and an iteratively optimized objective function in this study.
Moreover, we explore the hierarchical technique to build a hierarchy of clusters. There are two strategies for hierarchical clustering. One is agglomerative and the other is divisive. The agglomerative hierarchical clustering is a bottom-up manner in which each observation starts on its own cluster. Pairs of clusters are merged and move up the hierarchy. The divisive hierarchical clustering is a top-down manner in which all data start from one cluster. Splits are performed recursively, and data move down the hierarchy. We conducted the divisive hierarchical clustering in this study. To compare with the K-means clustering algorithm, the termination condition of the hierarchical method is specified by the desired number of K clusters.
B) Data normalization and selection
With clustering algorithms, the feature warping [Reference Pelecanos and Sridharan29] is performed using clustered feature vectors. A transformation function φ(.) is applied to convert features according to a lookup table. A lookup table is devised so as to map a rank order determined from the sorted cepstral feature elements to a warped feature using the desired warping target distribution. The feature warping is a kind of normalization process used to map a feature stream to a standard normal distribution. This process effectively Gaussianises the distribution of selected feature vectors so as to better fit to Gaussian assumptions in the model training and testing. The similar technique such as histogram equalization (HEQ) is commonly used in image processing and speech recognition [Reference Torre, Peinado, Segura, Perez-Cordoba, Bentez and Rubio30,Reference Huang, Tsao, Hori and Kashioka31].
For the training of ensemble clusters of the unsupervised data selection, the UBM training dataset is utilized. The created clusters are then used to split the following data into subsets: UBM training, score normalization, speaker enrollment, and testing. The ensemble-based speaker recognition systems are trained and tested with the corresponding subsets. Because the selection of number K may lead to a data sparsity problem in the training and the testing of speaker recognition, we study different numbers of K in our experiments.
C) Combination of ensemble classifiers
We usually consult several experts before making an important decision in daily life. Ensemble-based systems weigh several opinions and combine them to reach a final decision instead of a single-expert system [Reference Polikar32,Reference Rokach33]. Figure 3 illustrates the proposed ensemble classifiers for speaker recognition based on the divide-and-conquer strategy. The original speech data are segmented into several data subsets from which ensemble-based speaker recognition systems are trained and tested by non-overlapping segmentations.

Fig. 3. Testing procedure of ensemble classifiers using unsupervised data selection.
We consider two factors for building the ensemble-based speaker recognition. One is to cluster and select data based on acoustic variability. The other is to combine the results of ensemble classifiers. In this study, the frame counts (FCs) of the subsets are used as the weights for a combination of ensemble classifiers. With conventional GMM–UBM architecture, the speaker recognition decision is based on the log-likelihood ratio (LLR) between target speaker GMM λ SPK and UBM λ UBM .
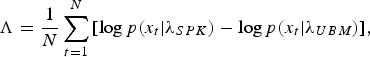 $$\Lambda ={{1}\over{N}}\sum\limits_{t=1}^N {[\log p(x_t \vert \lambda _{SPK} )} -\log p(x_t \vert \lambda _{UBM} )], $$
$$\Lambda ={{1}\over{N}}\sum\limits_{t=1}^N {[\log p(x_t \vert \lambda _{SPK} )} -\log p(x_t \vert \lambda _{UBM} )], $$
where N means the total frames. If the score exceeds threshold
![]() $\Lambda > {\theta }$
, then the claimed speaker will be accepted, or else rejected. To exploit the ensemble classifiers in the GMM–UBM architecture, the proposed LLR score
$\Lambda > {\theta }$
, then the claimed speaker will be accepted, or else rejected. To exploit the ensemble classifiers in the GMM–UBM architecture, the proposed LLR score
![]() $\tilde{\Lambda}$
considering the FC is then estimated as follows:
$\tilde{\Lambda}$
considering the FC is then estimated as follows:
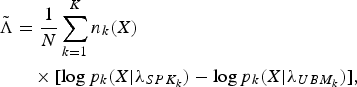 $$\eqalign{\tilde {\Lambda }&={1 \over N}\sum\limits_{k=1}^K {n_k (X)}\cr & \quad \times \lsqb {\log p_k (X\vert \lambda_{SPK_k } )-\log p_k (X\vert \lambda_{UBM_k } )} \rsqb ,} $$
$$\eqalign{\tilde {\Lambda }&={1 \over N}\sum\limits_{k=1}^K {n_k (X)}\cr & \quad \times \lsqb {\log p_k (X\vert \lambda_{SPK_k } )-\log p_k (X\vert \lambda_{UBM_k } )} \rsqb ,} $$
where n
k
(X) is the number of frames in classifier k and satisfies
![]() $\sum\nolimits_{k=1}^{K} {n_{k} (X)/N} =1$
. In other words, the contribution of ensemble classifier k is zero if the FC n
k
(X) is zero. Equations (8) and (9) indicate that LLR was calculated only on the test data. x
t
in equation (8) and X in equation (9) represent the test data. Given the test data X and subset k GMM, we can estimate the likelihood,
$\sum\nolimits_{k=1}^{K} {n_{k} (X)/N} =1$
. In other words, the contribution of ensemble classifier k is zero if the FC n
k
(X) is zero. Equations (8) and (9) indicate that LLR was calculated only on the test data. x
t
in equation (8) and X in equation (9) represent the test data. Given the test data X and subset k GMM, we can estimate the likelihood,
![]() $p_{k} (X\vert \lambda _{UBM_{k} })$
, and then know n
k
(X). Base on the same idea, in the ensemble method of i-vector, cosine scores of subsets are combined with the average weighted sum which considering the FC.
$p_{k} (X\vert \lambda _{UBM_{k} })$
, and then know n
k
(X). Base on the same idea, in the ensemble method of i-vector, cosine scores of subsets are combined with the average weighted sum which considering the FC.
V. EXPERIMENT PROTOCOL
The NIST SRE data were collected from different types of channel as telephones and microphones. We evaluated the system on the core condition of the 2010 NIST SRE in the tel–tel condition (det5) [34]. In this section, we apply three speaker recognition systems based on MAP, eigenchannel, and i-vector for evaluating the proposed approach.
A) Baseline systems
The NIST SRE-2004, SRE-2005, and SRE-2006 one-side data were used to train gender-dependent UBMs. The speaker adaptation techniques are used to solve speaker data sparseness and channel mismatch problems. MAP [Reference Bimbot3] is a popular approach to adapt speaker model from UBM. To further consider various channel factors, the eigenchannel adaptation [Reference Kenny, Boulianne, Ouellet and Dumouchel4] provides a good solution for channel mismatch. The eigenchannel assumes the means of the speaker's model are given by
![]() $\bf{m}_{SPK} =\bf{m}_{UBM} +\bf{Uh}$
, while m
UBM
denotes the supervector of the concatenation of UBM means, U is a rectangular low-rank matrix in which the columns are the numbers of directions of channel variability, and h is a normally distributed random vector that is learned from samples. The SRE-2004, SRE-2005, and SRE-2006 data were used to derive the eigenchannel estimation. The channel factor was set to 40 in this study.
$\bf{m}_{SPK} =\bf{m}_{UBM} +\bf{Uh}$
, while m
UBM
denotes the supervector of the concatenation of UBM means, U is a rectangular low-rank matrix in which the columns are the numbers of directions of channel variability, and h is a normally distributed random vector that is learned from samples. The SRE-2004, SRE-2005, and SRE-2006 data were used to derive the eigenchannel estimation. The channel factor was set to 40 in this study.
The fast-scoring technique was applied by approximating likelihood values using the top five mixture components [Reference Reynolds, Quatieri and Dunn35]. The outputs of MAP and eigenchannel systems were normalized with ZT-norm to further compensate for the nuisance effects, in which T-norm [Reference Auckenthaler, Carey and Lloyd-Thomas36] is first applied and then Z-norm [Reference Li and Porter37] speaker models are tested by imposters’ speech utterances. With T-norm, the input test speech utterance is evaluated against cohort models to obtain normalization scores using mean and standard deviation. With Z-norm, a speaker model is tested against imposter speech utterances to obtain the mean and standard deviation scores of normalization. For run-time efficiency, Z-norm can be estimated in an offline mode. In this study, 50 speakers are randomly selected from the NIST SRE-2004, SRE-2005, and SRE-2006 one-side data for Z-norm and non-overlapped 50 speakers for T-norm.
Furthermore, the i-vector system has become one of the state-of-the-art techniques in speaker verification applications [Reference Dehak, Kenny, Dehak, Dumouchel and Ouellet5]. The i-vector estimation assumes the speaker and channel-dependent GMM mean supervector is given by
![]() $\bf{m}_{SPK} =\bf{m}_{UBM} +\bf{Tw}$
, while T is a rectangular low-rank matrix representing R bases spanning subspace with important variability in the GMM mean supervector space, and w is a normally distributed random vector of size R that is learned from the samples. We termed the vector weighting w as i-vector and selected the dimension R=200 for the speaker recognition evaluation. To minimize the effect of within-speaker covariances, we applied the within-class covariance normalization (WCCN) transform in i-vector space to find the transformed vector
$\bf{m}_{SPK} =\bf{m}_{UBM} +\bf{Tw}$
, while T is a rectangular low-rank matrix representing R bases spanning subspace with important variability in the GMM mean supervector space, and w is a normally distributed random vector of size R that is learned from the samples. We termed the vector weighting w as i-vector and selected the dimension R=200 for the speaker recognition evaluation. To minimize the effect of within-speaker covariances, we applied the within-class covariance normalization (WCCN) transform in i-vector space to find the transformed vector
![]() ${\hat{w}}= {B}^{T}\bf{w}$
. The transform matrix B is derived from the Cholesky decomposition of W = BB
T
, where w is the within-speaker covariance matrix estimated by
${\hat{w}}= {B}^{T}\bf{w}$
. The transform matrix B is derived from the Cholesky decomposition of W = BB
T
, where w is the within-speaker covariance matrix estimated by
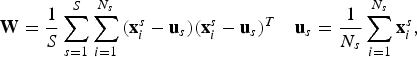 $${\bf{W}}={1\over S}\sum\limits_{s=1}^S {\sum\limits_{i=1}^{N_s}{({\bf{x}}_i^s -{\bf{u}}_s )({\bf{x}}_i^s -{\bf{u}}_s )^T} } \quad {\bf{u}}_s ={1\over {N_{s} }}\sum\limits_{i=1}^{N_s } {{\bf{x}}_i^s}, $$
$${\bf{W}}={1\over S}\sum\limits_{s=1}^S {\sum\limits_{i=1}^{N_s}{({\bf{x}}_i^s -{\bf{u}}_s )({\bf{x}}_i^s -{\bf{u}}_s )^T} } \quad {\bf{u}}_s ={1\over {N_{s} }}\sum\limits_{i=1}^{N_s } {{\bf{x}}_i^s}, $$
where S is the number of speakers, each having N
s
i-vectors. Switchboard II, SRE-2004, SRE-2005, and SRE-2006 data were used to derive the estimation of T. WCCN was estimated only on SRE-2004, SRE-2005, and SRE-2006 data. In addition, we apply the simple technique of normalizing i-vector to the unit length by capturing their directions,
![]() ${\bar{\bf{w}}}= {\hat{\bf{w}}}/\left\| {{\hat{\bf{w}}}} \right\|$
.
${\bar{\bf{w}}}= {\hat{\bf{w}}}/\left\| {{\hat{\bf{w}}}} \right\|$
.
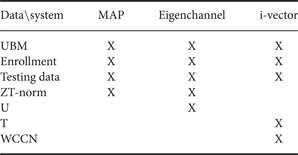
As we discussed earlier, the speech data were divided into several subsets using unsupervised data selection. Table 1 summarized the dataset (or parameters) used for ensemble classifiers based on different evaluation systems.
Table 1. Data (or parameters) used for ensemble classifiers based on different evaluation systems.
B) Performance evaluation
Two types of errors, false acceptance and false rejection, can occur in speaker verification. Equal error rate (EER) reports the system performance when the false acceptance
![]() $P_{{FalseAlarm}\vert {NonTarget}} $
and false rejection rates
$P_{{FalseAlarm}\vert {NonTarget}} $
and false rejection rates
![]() $P_{Miss\vert Target} $
are equal. The minimum Detection Cost Function (DCF) is a weighed sum of miss detection and false alarm rates as defined in NIST SRE-2010 [Reference Rokach33], and shown as follows:
$P_{Miss\vert Target} $
are equal. The minimum Detection Cost Function (DCF) is a weighed sum of miss detection and false alarm rates as defined in NIST SRE-2010 [Reference Rokach33], and shown as follows:
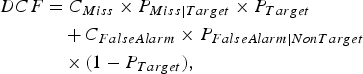 $$\eqalign{DCF &=C_{Miss} \times P_{Miss\vert Target} \times P_{Target}\cr & \quad +C_{FalseAlarm} \times P_{FalseAlarm\vert NonTarget}\cr & \quad \times (1-P_{Target}),} $$
$$\eqalign{DCF &=C_{Miss} \times P_{Miss\vert Target} \times P_{Target}\cr & \quad +C_{FalseAlarm} \times P_{FalseAlarm\vert NonTarget}\cr & \quad \times (1-P_{Target}),} $$
where
![]() $C_{\bf{Miss}} =10$
,
$C_{\bf{Miss}} =10$
,
![]() $C_{\bf{FalseAlarm}} =0.001,$
and
$C_{\bf{FalseAlarm}} =0.001,$
and
![]() $P_{\bf{Target}} =1$
were defined in SRE-2010. The speaker verification results were reported in terms of 1000 × DCF for SRE-2010 in this study. The following results were given on the EER and the minimum DCF point.
$P_{\bf{Target}} =1$
were defined in SRE-2010. The speaker verification results were reported in terms of 1000 × DCF for SRE-2010 in this study. The following results were given on the EER and the minimum DCF point.
VI. RESULTS AND ANALYSIS
We evaluated the robustness of the ensemble classifiers using unsupervised data selection from several viewpoints. LTF4 was used for all the experiments, which is with four long-term windows.
A) Unsupervised data selection
To determine the effect of unsupervised data selection and the ensemble classifiers, we first compared K-means (K) and hierarchical (H) clustering algorithms based on Mahalanobis distance metric, and weighting schemes using equal weighting (EW) and FCs. The summarized results were shown in Table 2. Four subsets (k=4) were used for the ensemble classifiers with MAP and ZT-norm. The mixture number of UBMs was 256. The baseline system was trained and tested with all data, which means it is the conventional single classifier. The results showed that the K-means clustering algorithm outperformed the hierarchical and baseline systems. The combination of ensemble classifiers with a weighting scheme of FCs was better than EW.
Table 2. Results of ensemble classifiers using different clustering and weighting schemes on MAP and ZT-norm systems on NIST SRE-2010.

Base on K-means clustering algorithm and a weighting scheme of FCs, we conducted ensemble systems using different similarity metrics to compare with the baseline system. We explored five similarity measures, log-likelihood measure, delta-BIC measure, cosine measure, Euclidean, and Mahalanobis distance measure, to construct partitioning clusters. The summarized results were shown in Table 3. We found that ensemble-based speaker recognition showed improvements with suitable data selection scheme, such as cosine and Mahalanobis distance metrics. Since we conventionally focus on minimizing DCF score, the best performance was shown on the Mahalanobis distance metric. Comparing the baseline system, the ensemble-based speaker recognition contributed to 8.51% relative EER reduction from 10.81 to 9.89, and 15.29% relative DCF reduction from 0.85 to 0.72.
Table 3. Results of ensemble classifiers using different distance metrics on MAP and ZT-norm systems on NIST SRE-2010.

We evaluated the conversational telephone English speech of the SRE-2008 core task based on the optimized setting obtained from the SRE-2010 data using version 3 of the NIST SRE-2008 answer keys. Four subsets were used for the ensemble classifiers with MAP and ZT-norm. The mixture number of UBMs was 256. We had the same improvements shown in Table 4. Comparing with the baseline system, the ensemble-based speaker recognition using the Mahalanobis distance metric contributed to 11.52% relative EER reduction from 7.55 to 6.68, and 16.87% relative DCF reduction from 3.32 to 2.76 on the SRE-2008 data. Motivated by the advanced channel and speaker adaptation techniques, we further extend the proposed ensemble-based speaker recognition to eigenchannel and i-vector approaches.
Table 4. Results of ensemble classifiers using different distance metrics on MAP and ZT-norm systems on NIST SRE-2008.

B) Ensemble-based eigenchannel systems
Experiment results of the ensemble-based eigenchannel system with ZT-norm are shown in Fig. 4. We conducted experiments on four different numbers of UBM mixtures including 128, 256, 512, and 1024 with four subsets. Four subsets were used for ensemble classifiers with the Mahalanobis distance metric. In Fig. 4, the blue and dashed line showed the eigenchannel approach. The red and solid line showed the proposed ensemble classifiers with the eigenchannel adaptation.

Fig. 4. DCF curves of eigenchannel with ZT-norm systems with different numbers of UBM mixtures on NIST SRE-2010.
Compared with results shown in Table 2, large gains were obtained using the eigenchannel technique. Eigenchannel with ZT-norm showed the effect of good channel compensation and score normalization. Our proposed ensemble-based approach can be further used for improving the overall performance. Basically, we can found that the DCF score decreased when the number of UBM mixture increased. In Fig. 4, UBM with 256 mixtures achieved the lowest DCF scores.
We achieved 19.64% relative DCF reduction from 0.56 to 0.45 (or 16.67% relative DCF reduction from 0.54 to 0.45) using the ensemble-based eigenchannel system with the UBMs of 256 mixtures. To further explore the relations between the number of mixture in UBM and the number of data subsets in ensemble, we conducted experiments with five different numbers of data subsets (2, 4, 8, 16, and 32) on four different numbers of UBM mixtures (128, 256, 512, and 1024) shown in Fig. 5. Due to data sparsity, a smaller number of subsets in the ensemble should be applied if a larger size of UBM mixtures is adopted. As a result, we can find that UBM of 128 mixtures with eight subsets, UBM of 256 and 512 mixtures with four subsets, and UBM of 1024 mixtures with two subsets achieved the lowest DCF scores. The best performance was located on UBM of 256 mixtures with four subsets. Based on these best setting, we further applied ensemble classifiers on the i-vector-based speaker recognition system in the following experiments.

Fig. 5. DCF curves of eigenchannel with ZT-norm systems with different numbers of UBM mixtures and data subsets on NIST SRE-2010.
C) Ensemble-based i-vector systems
The evaluation results of SRE-2010 were shown in Table 5 based on the i-vector system. The proposed ensemble-based systems using unsupervised data selection outperformed the conventional i-vector approach. Comparing the baseline system, the ensemble-based i-vector system contributed to 9.36% relative EER reduction from 4.38 to 3.97, and 5.26% relative DCF reduction from 0.57 to 0.54% on the SRE-2010 data. Experimental results of SRE-2008 data were shown in Table 6. The experiment confirmed that ensemble classifiers consistently improved the speaker recognition performance. Since original speech data were segmented into several data subsets according to acoustic characteristics on training and testing, we were able to train and test a more robust speaker recognition system.
Table 5. Results of I-Vector system with and without ensemble classifiers on NIST SRE-2010.
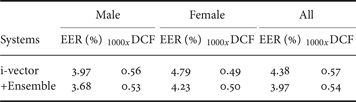
Table 6. Results of i-vector system with and without ensemble classifiers on NIST SRE-2008.

Fusion of LTFs showed further improvement. We apply the same kind of MFCC features with the different size of the long-term windows, L= 4, 6, 8 frames, namely LTF4, LTF6, and LTF8 [Reference Jacobs, Jordan, Nowlan and Hinton16]. Table 7 showed the fusion results of SRE-2010 and SRE-2008 considering features of LTF4, LTF6, and LTF8. Fusion weights were selected as 0.5, 0.3, and 0.2, respectively. The results showed that the fusion was complementary. The evaluations of SRE-2010 were plotted with the DET curves in Fig. 6. Regarding the i-vector systems, the scoring method used cosine similarity. We apply LTF on i-vector estimation and i-vector is used for unsupervised clustering. In addition, we used ensemble-based system for fusion of LTFs.

Fig. 6. DET curves showing improvements of conventional i-vector system, ensemble-based system, fusion of LTF system on SRE-2010.
Table 7. fusion of ensemble based I-Vector system with LTFs on NIST SRE-2010 and SRE-2008.

VII. CONCLUSION
We studied the ensemble method using unsupervised data selection for effective speaker recognition. Unlike previous constrain approaches, we had no auxiliary information requirement. The speech data were divided into several subsets using K-means clustering algorithm with the Mahalanobis distance metric and the FC weighting scheme. There are many clustering algorithms. In this study, we compared K-means and HAC to discover the effect of clustering algorithms and unsupervised data selection. With the divide-and-conquer strategy, ensemble classifiers were used to avoid the local optimization training on the single classifier. We studied feature extraction techniques using long-term and temporal information for effective speaker recognition, and trained and evaluated the ensemble classifiers based on the selected data subsets. Using the LTF and the ensemble method decreases the amount of data for training, because the LTF provides the more compact feature and the ensemble method divides data into subsets. Three speaker recognition experiments based on MAP, eigenchannel, and i-vector on the NIST SRE-2010 and SRE-2008 datasets were conducted. Based on the experiment results, we confirm that the ensemble classifiers with unsupervised data selection consistently improve the speaker recognition performance on different evaluation tasks and systems.
Chien-Lin Huang received the Ph.D. degree in Computer Science and Information Engineering from National Cheng Kung University, Taiwan, in 2008. He is a speech scientist at Voicebox Technologies currently. Before, he was a scientist in Japan NICT and Singapore I2R, respectively. Chien-Lin's research focuses on speech recognition, speaker recognition, and speech retrieval. He is an active member of speech and language processing communities. He has co-authored over 40 technical papers and holds 2 U.S. patents.
Jia-Ching Wang received the Ph.D. degree in Electrical Engineering from National Cheng Kung University, Tainan, Taiwan. He currently works at Department of Computer Science and Information Engineering, National Central University, Jhongli, Taiwan, as an associate professor. He was an honorary fellow at Department of Electrical and Computer Engineering, University of Wisconsin-Madison, WI, USA, during 2008 and 2009. His research interests include multimedia signal processing and associated VLSI architecture design. He is an honorary member of Phi Tau Phi Scholastic Honor Society and a senior member of IEEE.
Bin Ma received the B.Sc. degree in Computer Science from Shandong University, China, in 1990, the M.Sc. degree in Pattern Recognition & Artificial Intelligence from the Institute of Automation, Chinese Academy of Sciences (IACAS), China, in 1993, and the Ph.D. degree in Computer Engineering from The University of Hong Kong, in 2000. He was a Research Assistant from 1993 to 1996 at the National Laboratory of Pattern Recognition in IACAS. In 2000, he joined Lernout & Hauspie Asia Pacific as a Researcher working on speech recognition. From 2001 to 2004, he worked for InfoTalk Corp., Ltd, as a Senior Researcher and a Senior Technical Manager for speech recognition. He joined the Institute for Infocomm Research, Singapore in 2004 and is now working as a Senior Scientist and the Lab Head of Automatic Speech Recognition. He has served as a Subject Editor for Speech Communication in 2009–2012, the Technical Program Co-Chair for INTERSPEECH 2014, and is now serving as an Associate Editor for IEEE/ACM Transactions on Audio, Speech, and Language Processing. His current research interests include robust speech recognition, speaker & language recognition, spoken document retrieval, natural language processing and machine learning.














