Article contents
Sigmoidal cosine series on the interval
Published online by Cambridge University Press: 17 February 2009
Abstract
We construct a set of functions, say, 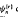 composed of a cosine function and a sigmoidal transformation γr of order r > 0. The present functions are orthonormal with respect to a proper weight function on the interval [−1, 1]. It is proven that if a function f is continuous and piecewise smooth on [−1, 1] then its series expansion based on
composed of a cosine function and a sigmoidal transformation γr of order r > 0. The present functions are orthonormal with respect to a proper weight function on the interval [−1, 1]. It is proven that if a function f is continuous and piecewise smooth on [−1, 1] then its series expansion based on 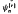 converges uniformly to f so long as the order of the sigmoidal transformation employed is 0 < r ≤ 1. Owing to the variational feature of
converges uniformly to f so long as the order of the sigmoidal transformation employed is 0 < r ≤ 1. Owing to the variational feature of 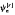 according to the value of r, one can expect improvement of the traditional Fourier series approximation for a function on a finite interval. Several numerical examples show the efficiency of the present series expansion in comparison with the Fourier series expansion.
according to the value of r, one can expect improvement of the traditional Fourier series approximation for a function on a finite interval. Several numerical examples show the efficiency of the present series expansion in comparison with the Fourier series expansion.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2006
References
- 1
- Cited by

