No CrossRef data available.
Article contents
CHARACTERIZATIONS OF THE BOREL 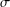 $\unicode[STIX]{x1D70E}$ -FIELDS OF THE FUZZY NUMBER SPACE
$\unicode[STIX]{x1D70E}$ -FIELDS OF THE FUZZY NUMBER SPACE
Published online by Cambridge University Press: 15 May 2017
Abstract
In this paper, we characterize Borel 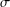 $\unicode[STIX]{x1D70E}$ -fields of the set of all fuzzy numbers endowed with different metrics. The main result is that the Borel
$\unicode[STIX]{x1D70E}$ -fields of the set of all fuzzy numbers endowed with different metrics. The main result is that the Borel 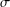 $\unicode[STIX]{x1D70E}$ -fields with respect to all known separable metrics are identical. This Borel field is the Borel
$\unicode[STIX]{x1D70E}$ -fields with respect to all known separable metrics are identical. This Borel field is the Borel 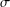 $\unicode[STIX]{x1D70E}$ -field making all level cut functions of fuzzy mappings from any measurable space to the fuzzy number space measurable with respect to the Hausdorff metric on the cut sets. The relation between the Borel
$\unicode[STIX]{x1D70E}$ -field making all level cut functions of fuzzy mappings from any measurable space to the fuzzy number space measurable with respect to the Hausdorff metric on the cut sets. The relation between the Borel 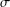 $\unicode[STIX]{x1D70E}$ -field with respect to the supremum metric
$\unicode[STIX]{x1D70E}$ -field with respect to the supremum metric 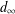 $d_{\infty }$ is also demonstrated. We prove that the Borel field is induced by a separable and complete metric. A global characterization of measurability of fuzzy-valued functions is given via the main result. Applications to fuzzy-valued integrals are given, and an approximation method is presented for integrals of fuzzy-valued functions. Finally, an example is given to illustrate the applications of these results in economics. This example shows that the results in this paper are basic to the theory of fuzzy-valued functions, such as the fuzzy version of Lebesgue-like integrals of fuzzy-valued functions, and are useful in applied fields.
$d_{\infty }$ is also demonstrated. We prove that the Borel field is induced by a separable and complete metric. A global characterization of measurability of fuzzy-valued functions is given via the main result. Applications to fuzzy-valued integrals are given, and an approximation method is presented for integrals of fuzzy-valued functions. Finally, an example is given to illustrate the applications of these results in economics. This example shows that the results in this paper are basic to the theory of fuzzy-valued functions, such as the fuzzy version of Lebesgue-like integrals of fuzzy-valued functions, and are useful in applied fields.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2017 Australian Mathematical Society

