Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-28T23:31:34.630Z Has data issue: false hasContentIssue false
  • English
  • Français

Assessing regularised solutions

Published online by Cambridge University Press:  17 February 2009

M. A. Lukas
M. A. Lukas
Affiliation:
School of Mathematical and Physical Sciences, Murdoch University, Murdoch, W. A. 6150, Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the prototype ill-posed problem of a first kind integral equation ℛ with discrete noisy data di, = f(xi) + εi, i = 1, …, n. Let u0 be the true solution and unα a regularised solution with regularisation parameter α. Under certain assumptions, it is known that if α → 0 but not too quickly as n → ∞, then unα converges to u0. We examine the dependence of the optimal sequence of α and resulting optimal convergence rate on the smoothness of f or u0, the kernel K, the order of regularisation m and the error norm used. Some important implications are made, including the fact that m must be sufficiently high relative to the smoothness of u0 in order to ensure optimal convergence. An optimal filtering criterion is used to determine the order 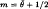where 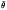is the maximum smoothness of u0. Two practical methods for estimating the optimal α, the unbiased risk estimate and generalised cross validation, are also discussed.

Type
Research Article
Information
The ANZIAM Journal , Volume 30 , Issue 1 , July 1988 , pp. 24 - 42
Copyright
Copyright © Australian Mathematical Society 1988

References

[1]Anderssen, R. S., “Application and numerical solution of Abel-type integral equations”, MRC Technical Summary Report No. 1987, University of Wisconsin-Madison (1977).Google Scholar
[2]Cox, D. D., “Approximation of method of regularisation estimators”, University of Wisconsin-Madison, Department of Statistics, Technical Report No. 723 (1983).Google Scholar
[3]Craven, P. and Wahba, G., “Smoothing noisy data with spline functions: estimating the correct degree of smoothing by the method of generalised cross-validation”, Numer. Math. 31 (1979) 377–403.CrossRefGoogle Scholar
[4]Cullum, J., “The effective choice of the smoothing norm in regularisation”, Math. Comp. 33 (1979) 149–170.CrossRefGoogle Scholar
[5]Davies, A. R. and Anderssen, R. S., “Optimisation in the regularisation of ill-posed problems”, J. Austral. Math. Soc. Ser. B 28 (1986) 114–133.CrossRefGoogle Scholar
[6]Davies, A. R. and Anderssen, R. S., “Improved estimates of statistical regularisation parameters in Fourier differentiation and smoothing”, Numer. Math. 48 (1986) 671–697.CrossRefGoogle Scholar
[7]de Hoog, F. R., “Review of Fredholm equations of the first kind”, in The application and numerical solution of integral equations (eds. Anderssen, R. S., de Hoog, F. R. and Lukas, M. A.), (Sijthoff & Noordhoff, 1980).Google Scholar
[8]Gehatia, M. and Wiff, D. R., “Solution of Fujita's equation for equilibrium sedimentation by applying Tikhonov's regularising functions”, J. Polymer Science: Part A-2 8 (1970) 2039–2050.Google Scholar
[9]Lukas, M. A., “Regularisation”, in The application and numerical solution of integral equations (eds. Anderssen, R. S., de Hoog, F. R. and Lukas, M. A.), (Sijthoff & Noordhoff, 1980).Google Scholar
[10]Lukas, M. A., “Regularisation of linear operator equations”, Ph.D. Thesis, Australian National University, Canberra (1981).CrossRefGoogle Scholar
[11]Lukas, M. A., “Convergence rates for regularised solutions”, to appear in Math. Comp. (1988).CrossRefGoogle Scholar
[12]Lukas, M. A., “Optimal filtering and the order of regularisation”, in preparation.Google Scholar
[13]Lukas, M. A., “Asymptotic behaviour of practical estimates of the regularisation parameter”, in preparation.Google Scholar
[14]Nashed, M. Z. and Wahba, G., “Generalised inverses in reproducing kernel spaces: an introduction to regularisation of linear operator equations”, SIAM J. Math. Anal. 5 (1974) 974–987.CrossRefGoogle Scholar
[15]Natterer, F., “Error bounds for Tikhonov regularisation in Hilbert scales”, Applicable Anal. 18 (1984) 29–37.CrossRefGoogle Scholar
[16]Newsam, G. N., “Measures of information in linear ill-posed problems”, Australian National University, Centre for Mathematical Analysis, Research Report No. 28 (1984).Google Scholar
[17]Rice, J. and Rosenblatt, M., “Smoothing splines: regression, derivatives and deconvolution”, Ann. Statist. 11 (1983) 141–156.CrossRefGoogle Scholar
[18]Tikhonov, A. N. and Arsenin, V. Y., Solutions of Ill-Posed Problems (Wiley, 1977).Google Scholar
[19]Wahba, G., “Practical approximate solutions to linear operator equations when the data are noisy”, SIAM J. Numer. Anal. 14 (1977) 651–667.CrossRefGoogle Scholar
[20]Wahba, G., “Ill-posed problems: numerical and statistical methods for mildy, moderately and severely ill-posed problems with noisy data”, University of Wisconsin-Madison, Department of Statistics, Technical Report No. 595 (1980).Google Scholar
[21]Wahba, G., “A comparison of GCV and GML for choosing the smoothing parameter in the generalised spline smoothing problem”, Ann. Statist. 13 (1985) 1378–1402.CrossRefGoogle Scholar