Introduction
Glacier surface mass balance is directly linked to climatic conditions and is thus an excellent indicator of climate change (e.g. Reference Haeberli and BenistonHaeberli and Beniston, 1998). Monitoring the glacier mass budget using the direct glaciological method is, however, laborious and its application to remote, crevassed or large glaciers is hampered by problems with field site accessibility. This limits mass-balance observations to a relatively small sample of glaciers (Reference Haeberli, Zemp, Kaab, Paul and HoelzleWGMS, 2008) that might not be representative at the mountain-range scale (Reference HussHuss, 2012). Furthermore, direct observations of mass change mostly achieve only seasonal resolution (Reference Zemp, Hoelzle and HaeberliZemp and others, 2009). However, in analysing the importance of glacier melt contribution to the hydrological cycle, for instance, monthly mass-balance data would be useful. In order to extend glacier monitoring to a larger sample of glaciers, and also to those in mountain regions that are difficult to access, new methods are required that allow remote determination of seasonal to sub-seasonal mass balance.
Estimating glacier mass balance from remotely sensed information has a long tradition in glaciology. Reference LaChapelleLaChapelle (1962) proposed the use of aerial photography as an index for the glacier mass budget, and the equilibrium-line altitude (ELA), a variable observable without direct access to the glacier, is recognized as a valuable climate proxy (Reference AhlmannAhlmann, 1924; Reference Zemp, Hoelzle and HaeberliZemp and others, 2007). The calculation of glacier-wide annual mass balance from statistical relations with the ELA and the accumulation–area ratio (AAR) is well established, and has been applied in different mountain ranges (Reference KulkarniKulkarni, 1992; Reference ChinnChinn, 1995; Reference Chinn, Heydenrych and SalingerChinn and others, 2005; Reference Rabatel, Dedieu and VincentRabatel and others, 2005). However, ELA and AAR observations do not allow quantitative inference of seasonal mass balance, which is crucial for interpreting glacier sensitivity to climate change (e.g. Reference Ohmura, Bauder, Muller and KappenbergerOhmura and others, 2007). Moreover, glacier-wide mass balance can only be derived from ELA and AAR datasets for glaciers with long-term measurement series (Reference BraithwaiteBraithwaite, 1984).
The use of time-lapse photography and/or repeated satellite imagery has become an increasingly popular way to monitor snow-cover depletion patterns (e.g. Reference Parajka, Haas, Kirnbauer, Jansa and BloschlParajka and others, 2012), to validate models for basin hydrology (e.g. Reference Bloschl, Kirnbauer and GutknechtBloschl and others, 1991; Reference Turpin, Ferguson and ClarkTurpin and others, 1997) or permafrost distribution (Reference Mittaz, Imhof, Hoelzle and HaeberliMittaz and others, 2002), and to directly infer winter snow water equivalent from remotely sensed snow-cover distributions combined with melt modelling (Reference Martinec and RangoMartinec and Rango, 1981; Reference Molotch and MargulisMolotch and Margulis, 2008; Reference Farinotti, Magnusson, Huss and BauderFarinotti and others, 2010). Most studies, however, focus only on snow and its spatial distribution, and not on glacier mass balance.
Reference DyurgerovDyurgerov (1996) suggested estimating transient glacier-wide mass balances for several dates throughout the ablation season, based on the easily observable fraction of snow-covered glacier area using long-term relations between AAR and annual mass balance. Reference PeltoPelto (2011) used a similar approach to assess mass-balance changes near the ELA of Taku Glacier, Alaska, USA. In another application of this method Reference Hock, Kootstraa and ReijmerHock and others (2007) showed that determining transient mass balance from repeated snowline observations at Storglaciaren, Sweden, over 1 year is hampered by variations in winter accumulation, and that Dyurgerov’s approach is only applicable for a relatively limited range of transient AAR values.
This paper aims to combine the approaches to infer glacier-wide mass balance from ELA observations with techniques to calculate the spatial snow distribution from depletion patterns, and follows on from Reference Hock, Kootstraa and ReijmerHock and others (2007). We propose a new method that allows continuous monitoring of glacier surface mass balance over the summer season, based on repeated oblique glacier photography combined with mass-balance modelling. The fraction of snow-covered glacier surface is determined at sub-daily to weekly frequencies from orthorectified and georeferenced images from an automatic camera for Findelengletscher (2010 and 2011 melt seasons) and Gornergletscher (2004–09), two valley glaciers in the Swiss Alps. By merging this information with simple accumulation and melt modelling, the evolution of area-averaged glacier mass balance throughout the ablation period is calculated and validated against independent direct mass-balance observations. We demonstrate the potential of our simple methodology to derive mountain glacier mass balance at sub-seasonal resolution, without immediate field site access, based on terrestrial time-lapse photography or repeated satellite images.
Study Sites and Field Data
The development of our methodology is focused on Findelengletscher (glacier area 13.4 km2 in 2009), a valley glacier in the Southern Swiss Alps with a large and gently sloping accumulation area and a relatively narrow tongue (Fig. 1). There is no significant debris coverage on Findelen-gletscher. Since 2004, the mass balance of Findelengletscher has been measured in connection with a glacier-monitoring program maintained by the Universities of Fribourg and Zurich. Snow accumulation distribution measurements are available from helicopter-borne ground-penetrating radar in 2005 and 2010 (Reference Machguth, Eisen, Paul and HoelzleMachguth and others, 2006a; Reference Sold, Huss, Hoelzle, Joerg, Salzmann and ZempSold and others, 2012), and since 2009 from 300–700 point snow probings annually (Fig. 1). Annual mass balance is determined using the glaciological method based on measurements at a network of 11 stakes and 2 snow pits. The accuracy of glacier-wide winter balance is estimated as ±0.1 m w.e., and ±0.2 m w.e. for annual balance. In addition, repeated high-resolution digital elevation models (DEMs) are available from airborne laser scanning (lidar), providing the geodetic ice volume change between September 2009 and 2010 with an accuracy of ±0.05 m w.e. (Reference Joerg, Morsdorf and ZempJoerg and others, 2012).

Fig. 1. Overview map of the study site. The location of the automatic cameras at Findelengletscher and Gornergletscher and their field of view is shown. Sites with mass-balance measurements are indicated (winter accumulation: blue crosses; annual balance: red diamonds).
We test our approach on Gornergletscher (39.0 km2), the second largest glacier in the European Alps. The glacier system is connected to Findelengletscher in its accumulation area and consists of several branches. Gorner-gletscher descends from an elevation of >4500 m a.s.l. into a wide glacier tongue which is partly debris-covered. The confluence area of two tributary glaciers has been the subject of extensive studies between 2004 and 2009, related to the outbursts of a glacier-dammed lake (e.g. Reference Huss, Bauder, Werder, Funk and HockHuss and others, 2007; Reference Werder, Loye and FunkWerder and others, 2009). For Gornergletscher, ice ablation data between 2004 and 2007 at a network of up to 30 stakes are available on the glacier tongue; however, no measurements were performed in the accumulation area (Fig. 1). Long-term mass-balance time series (1908–2009) have been derived, based on a combination of observed multi-decadal ice volume change with mass-balance modelling, indicating a 100 year cumulative mass balance of -42 m w.e. (Reference Huss, Hock, Bauder and FunkHuss and others, 2010). Whereas these series are assumed to be relatively accurate for decadal periods, the year-to-year variability may be subject to uncertainties of up to ±0.38 m w.e. a - 1 (Reference Huss, Hock, Bauder and FunkHuss and others, 2010).
In April 2010, an automatic camera was installed on Unterrothorn (Fig. 1), a mountain overlooking the catchment of Findelengletscher (Fig. 2a). The camera takes pictures at hourly intervals that are directly transmitted to a server. Images are continuously available for the 2010 and 2011 melt seasons, with a short interruption in July 2010. The automatic camera on Gornergrat was operational between April 2004 and September 2009, providing one digital picture per day. The images miss the lower reaches of the Gornergletscher tongue, as well as some parts of the accumulation area. As a large elevation range is covered, it is still suitable for observing transient changes in the snowline (Fig. 2b).

Fig. 2. Example photographs from the automatic cameras overlooking (a) Findelengletscher and (b) Gornergletscher. The red line indicates the transient snowline at the date of the photograph; green lines show additional snowlines throughout the year.
Methods
Our methodology to estimate glacier-wide mass balance from oblique terrestrial photography requires (1) the detection of the transient snowline, (2) the orthorectification and georeferencing of the images and (3) the determination of the snow-covered area fraction (SCAF) relative to total glacier surface area. In a second step, SCAF values of repeated photographs throughout the ablation season are combined with simple distributed accumulation and melt modelling, in order to determine quantitative relations between transient snowline elevation and mass balance.
Snowline detection
We test two different methods for detecting the snowline in the images. In the first approach, the snowline is delineated manually, based on visual separation of bare-ice areas from snow-covered sections of the glacier (e.g. Fig. 2). This approach is robust, as it integrates the knowledge of the observer on snow-cover depletion patterns. However, small-scale snow cover variability is insufficiently resolved, and the processing time limits the number of treated images. We evaluate 11–18 pictures throughout each melt season for Gornergletscher (2004–09) and Findelengletscher (2010–11).
In the second approach, we analyse the entire image dataset for Findelengletscher between May and September 2011 (313 images with good visibility, i.e. no clouds hampering direct view of the glacier surface) using an algorithm to automatically map snow-covered and snow-free regions of the glacier surface, based on a self-adapting reflectance intensity threshold (Reference OtsuOtsu, 1979), that does not require additional information such as sensor sensitivity or reflectance reference fields. Daytime-dependent shading patterns are derived by stacking cloudless images taken at the same time. Using these fields, terrain shadows can be corrected before calculating the reflectance intensity thresholds. This automated approach provides classified images of the surface type (snow-covered or bare ice) within a mask defining the glacierized area (Fig. 3). The results of the automated snowline detection are quality-checked by evaluating the standard deviation of snow-classified pixels of all pictures within 1 day. Days with a standard deviation of >3% are discarded. The performance of this method is high on most days throughout the ablation season, with good visibility conditions and without patchy shadows cast by clouds, but is affected by summer snowfall events.

Fig. 3. Photographs of Findelengletscher taken on 28 June 2011. (a) Raw image and (b) automatically detected bare-ice areas (red).
Image georeferencing
In order to evaluate the areal percentage of the glacier covered with snow based on the oblique photograph, the image needs to be orthorectified and georeferenced. This is performed using a procedure developed by Reference CorripioCorripio (2004). Basically, the two-dimensional pixels of the photograph are related to three-dimensional points in the DEM by applying a perspective projection of the image pixels to the coordinate system of the DEM. Here, we use a lidar DEM acquired in 2009 that is resampled to a spatial resolution of 5 m for Findelengletscher (Reference Joerg, Morsdorf and ZempJoerg and others, 2012), and a 25 m DEM from 2003 based on aerial photogrammetry for Gornergletscher (Reference Bauder, Funk and HussBauder and others, 2007). The scaling functions between the camera perspective and the DEM are defined by matching the coordinates of five to seven ground-control points (mountain tops and other clearly defined landmarks) to the corresponding locations in the images. Shifts in the field of view are small and allowed us to maintain the same scaling functions for all images. The transformation results in a georeferenced orthoimage of reflectance values.
Determination of snow-covered area fraction
As a non-negligible fraction of the glacier area is invisible to the automatic camera (Findelengletscher: 29%, Gorner-gletscher: 49%), the observed surface type must be extrapolated to the entire glacier surface. This is done by determining the mean snowline elevation, based on the DEM, and assuming it to be the same in invisible regions of the glacier. Thus, for each picture, the SCAF relative to the total glacier area can be evaluated. SCAFs generally decrease from 100% in April to a minimum value at the end of the ablation season (September/October) and are then equal to the AAR.
We compared the manual and automatic approaches for delineating the snowlines in the camera images (Fig. 4). After quality-checking, automatically detected SCAFs were retained for 44 days throughout the 2011 ablation season (Findelengletscher), thus providing data for about every third day. The rise in the snowline during periods of strong melt that are not disrupted by fresh snowfall events (e.g. mid-June to July 2011) is clearly depicted. Towards the end of the ablation season, high-quality automatically detected SCAFs decrease in frequency (Fig. 4). The agreement of SCAFs obtained with the less detailed, more time-consuming, but robust manual snowline detection is within 1% for days with results for both methods.

Fig. 4. Comparison of automatically retrieved SCAF (blue triangles) with SCAF based on manually detected snowlines (black stars) in the 2011 ablation season (Findelengletscher). The error bar of the automatic SCAF refers to the standard deviation, σ, within multiple pictures taken on the same day. Automatic SCAF and derived mean snowline elevation (red diamonds) are only shown for days with σ < 3%. Bars indicate daily precipitation at Zermatt (scale shown at day of year 150).
The accuracy of the SCAF at a given date depends on (1) the snowline delineation uncertainty, (2) the DEM uncertainty, (3) the georeferencing and (4) the extrapolation to invisible parts of the glacier. The total uncertainty in the SCAF is quantified by performing an error assessment for each component. Based on the intercomparison of the two methods of snowline detection (Fig. 4), we estimate an impact of snowline delineation uncertainty on the SCAF of ±1%. The accuracy of the DEM used for the georeferencing determines the geolocation of the snowline. Tests using terrain elevation data shifted by 10 m showed that the SCAF is relatively insensitive (±0.2–0.5%) to uncertainties in the DEM due to the large camera–target distance. The spatial misfit of the ground-control points in the georeferenced image is 5–50 m, leading to a SCAF uncertainty of ±0.1–1%. Although a significant part of both glaciers is invisible to the camera, the sensitivity of the SCAF to snowline extrapolation into regions hidden from direct view is relatively small, as these are located in the upper accumulation area (Findelengletscher/Gornergletscher) or on the glacier tongue (Gornergletscher). Thus, throughout most of the year, the entire snowline is visible. We perform sensitivity tests for the assumptions used in the SCAF extrapolation to invisible glacier sections and find uncertainties of ±0.1–0.5%. Combining the potential sources of uncertainty (1)–(4) using error propagation, we estimate an integrated SCAF uncertainty increasing from 0.5% to 2.5% throughout the ablation season.
Linking SCAF to mass balance
Establishing the link between observed SCAF at a given date, t, and glacier-wide mass balance temporally integrated from the beginning of the hydrological year and t is not straightforward. The relation between SCAF and mass balance most importantly depends on the geometry of the glacier and the winter precipitation sums (see also Reference Hock, Kootstraa and ReijmerHock and others, 2007). Basically, the remote imagery provides the binary information whether the surface type of a pixel is snow or bare ice. In order to derive glacier mass change, a third dimension needs to be added, i.e. the height (the quantity) of snow accumulation or snow/ice ablation at a given location must be described. This can only be achieved by combining the remotely acquired snowline observations with a model for the spatial distribution of accumulation and ablation.
We aim to use a mass-balance model that is as simplified as possible, in order to ensure applicability to arbitrary glaciers without needing to calibrate with field data. In our case, two meteorological time series are available to drive the model, henceforth termed C1 and C2: (C1) Daily records of temperature and precipitation are taken from the valley station atZermatt (1634ma.s.l.; Fig. 1) for 2004-11. (C2)The climatological average of daily mean air temperature (196190) is provided by homogenized temperature series (Reference Begert, Schlegel and KirchhoferBegert and others, 2005) recorded at Sion (at 45 km distance). Data are scaled to the elevation of the glacier using monthly altitudinal temperature gradients obtained from all stations within a 30 km radius of the study site. Mean monthly precipitation sums are provided by a gridded precipitation map (Reference Schwarb, Daly, Frei and ScharSchwarb and others, 2001). Monthly precipitation is arbitrarily allocated to the daily series, such that each sixth day has 2 0% of the monthly precipitation total and the other days are dry. Series C2 could be derived from any climatological information (e.g. lowland stations, gridded climate reanalysis data), even for mountain ranges without a weather station network, and just prescribes the general pattern of temperature and precipitation seasonality.
We use a temperature-index approach (e.g. Reference BraithwaiteBraithwaite, 1995) that calculates melt, M(x,y), at daily temporal resolution for gridcell (x, y), based on a linear relation with daily mean air temperature, T(x, y), as
No melt occurs for T(x, y) < 0•C. DDFsnow/i c e are degree-day factors for snow and ice, for which we assume values DDFsnow = 4mmw.e. d - 1 and DDFice = 9 mmw.e. d - 1 , based on average values from previous studies (Reference HockHock, 2003). Temperature, T(x, y), is extrapolated to the elevation of the gridcell (given by the DEM) using a constant lapse rate of -6.5•Ckm-1.
Daily accumulation, C(x, y), is calculated using observed precipitation, P, corrected for gauge undercatch errors with a factor cprec and an altitudinal gradient dP/dz for the difference between the elevation of the gridcell, z(x, y), and the reference elevation of the meteorological series, zref, as
Precipitation occurring at temperatures higher than a threshold T t h r = 1.5•C is assumed to be in liquid form and is not added to mass balance. Above an elevation zcrit = 3300 m a.s.l. we assume no further increase in precipitation.
We propose a two-phase framework that allows the estimation of winter accumulation (phase 1), and glacier-wide mass balance (phase 2) based on repeated snowline observations. The workflow of this framework is sketched in Figure 5.
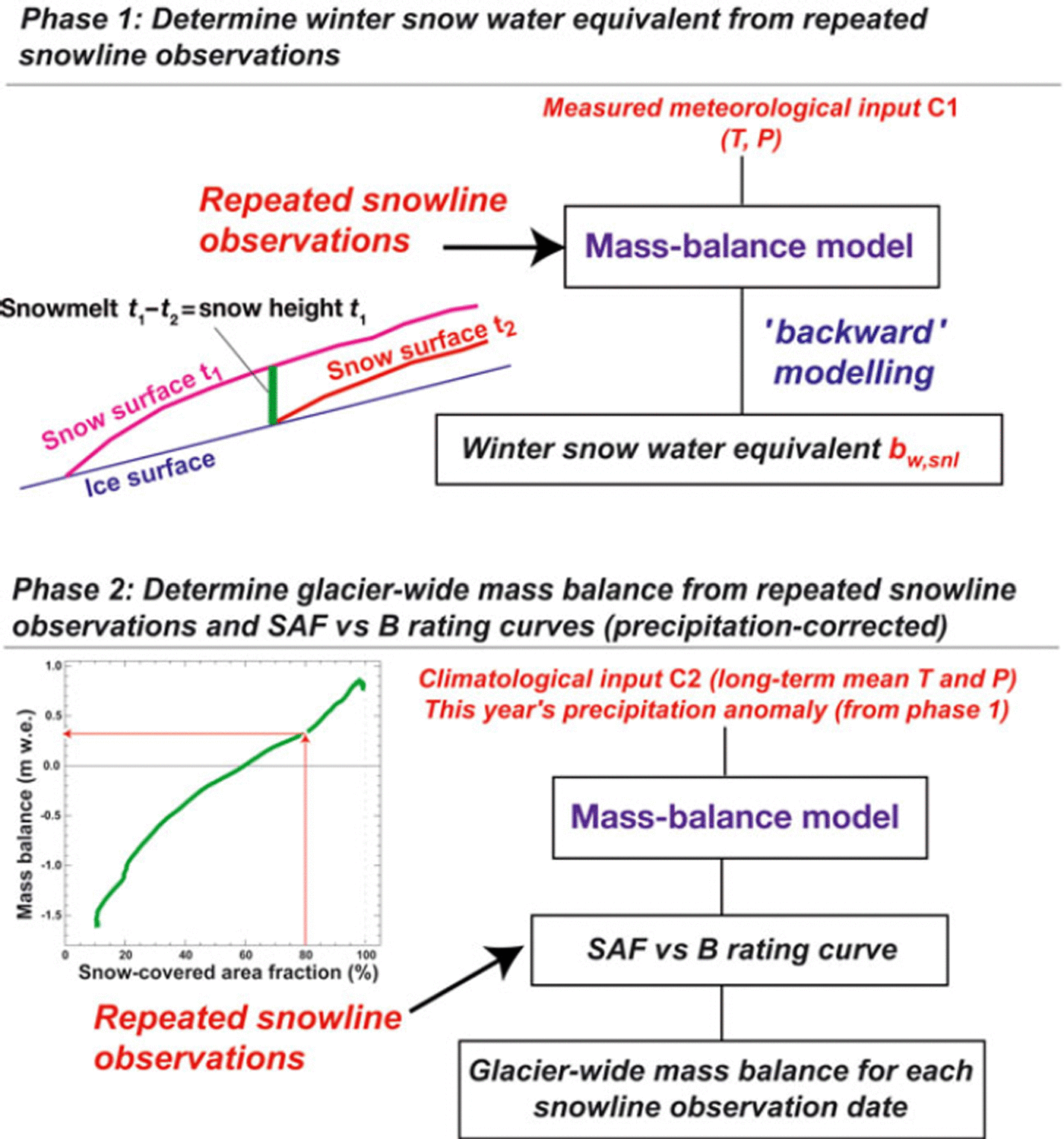
Fig. 5. Schematic representation of the approach to infer glacier-wide mass balance from repeated snowline observations. In phase 1 , winter snow accumulation, bw,snl, for different elevations on the glacier is determined by backward modelling based on observed changes in the snowline. A rating curve describing the relation between SCAF and glacier-wide transient mass balance is specifically derived for each glacier and the temperature and precipitation conditions of the investigated year in phase 2.
In phase 1, the winter snow accumulation is constrained by combining modelling with observed temporal changes in snow coverage (e.g. Reference Molotch and MargulisMolotch and Margulis, 2008; Reference Farinotti, Magnusson, Huss and BauderFarinotti and others, 2010). Considering a given location, (x, y), on the snowline at date t2, the local snow water equivalent for date t 1 equals the quantity of snowmelt between t1 and t2 (see also Reference PeltoPelto, 2011). Snowmelt between t1 and t2 is computed by the mass-balance model (Fig. 5) which is, in phase 1, driven by the meteorological series C1. Based on this backward-modelling approach, we infer the snow water equivalent at the beginning of the ablation season for several altitude bands corresponding to the location of individual snowline observations at different given dates, t2. This allows us to determine the quantity of winter snow accumulation for date t1 (i.e. the start of the ablation season) over the elevation ranging from the glacier terminus to that year’s ELA.
It is important to note that information on winter accumulation could also be obtained differently (e.g. by in situ snow measurements, by precipitation anomalies estimated from more distant weather station data or by running the model using the climatological series C2 instead of C1, thus circumventing the need for nearby meteorological time series).
Phase 2 addresses the calculation of a specific SCAF vs mass-balance rating curve using the mass-balance model. This rating curve describes the relation between modelled SCAF and glacier-wide transient mass balance, and accounts for the geometry of the investigated glacier. Figure 6 depicts typical rating curves for Findelengletscher for years with different precipitation anomalies. Mass balance for a given SCAF shows a significant dependence (maximal at the beginning of the melting season) on precipitation totals. Higher precipitation leads to a more positive mass balance for the same SCAF. Therefore, the estimate of winter accumulation from phase 1 is important for constructing a specific rating curve for each year (and each glacier) individually.
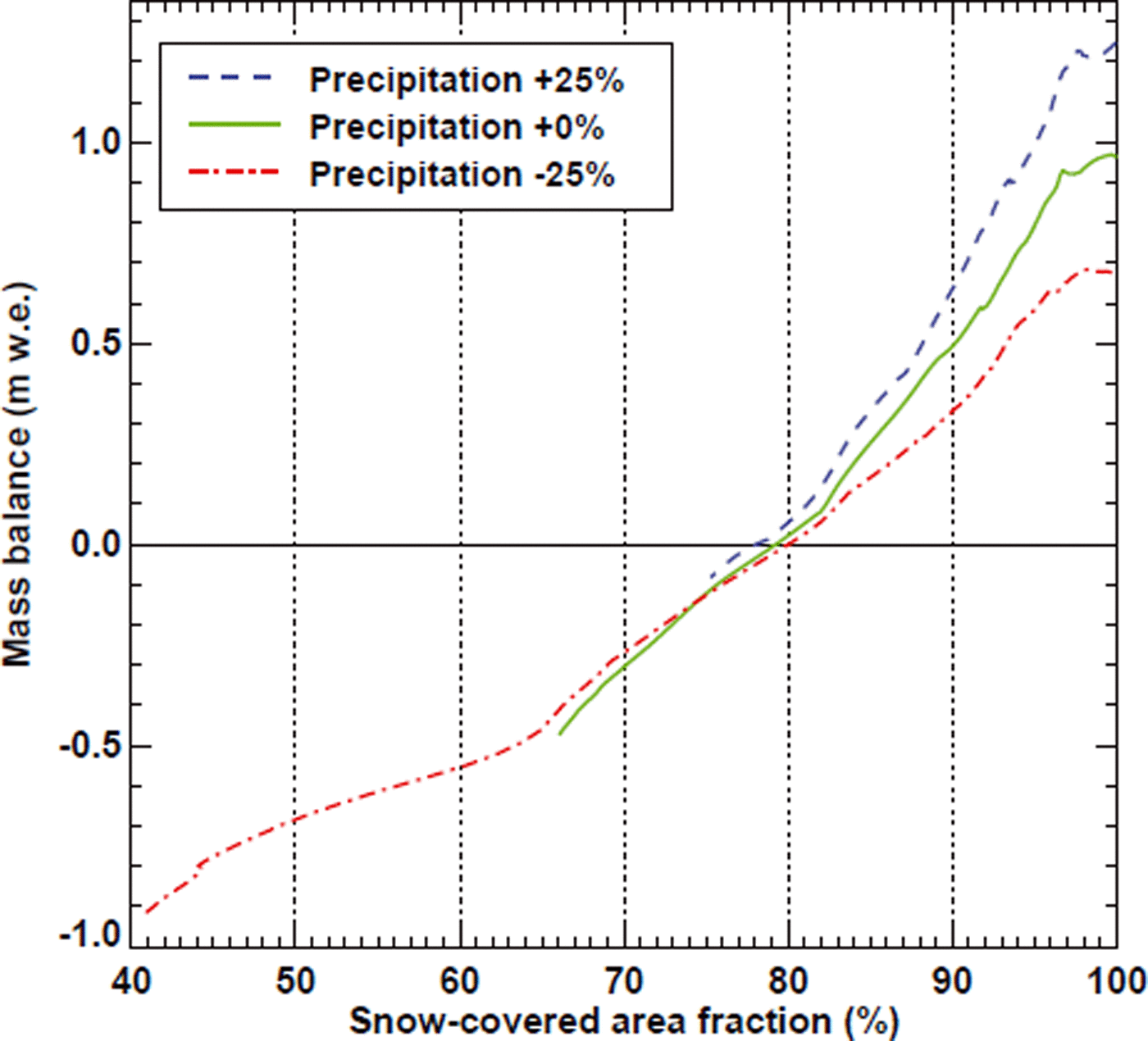
Fig. 6. Example rating curves of SCAF vs glacier-wide mass balance for Findelengletscher using different precipitation sums relative to a reference, but the same temperature forcing. Curves show the evolution of transient glacier-wide mass balance (relative to the beginning of the hydrological year) throughout the melt season. The end of the curves (i.e. the minimal SCAF) refers to the annual mass balance.
To this end, we run the mass-balance model using climatological series C2 of long-term average daily temperature and precipitation. This has the advantage that the calculated rating curve is unaffected by short-term meteorological variability and can even be derived if there are no nearby weather stations. We use constant values for the degree-day factors and the temperature gradient. The precipitation parameters cprec and dP/dz (Eqn (2)) are chosen such that the model results match the winter snow accumulation derived in phase 1 ; these parameters are thus updated for each year and are glacier-specific. In order to ensure that the rating curve covers the entire range of evaluated SCAF values, the climatological air temperature in series C2 is shifted so that modelled SCAF agrees with observed SCAF at the date of the last image. This corresponds to the correction of the temperature anomaly in the analysed year relative to the climatological mean given by series C2. Finally, a glacier-wide mass-balance estimate is derived for each SCAF observation date using the year- and glacier-specific rating function (Fig. 5). Thus, mass balance is directly obtained based on the SCAF which is observable on the terrestrial photographs; the model prescribes the general link between SCAF and mass balance.
Results
The SCAF varies considerably between given dates in individual years (Fig. 7), but the spatial pattern of snow depletion remains similar except for the change in timing. In mid-July 2006, only 59% of Gornergletscher was still covered with snow, compared to 74% at the same time in 2009. SCAFs for Findelengletscher are not directly comparable to Gornergletscher, due to different glacier geometries. Generally, meltout starts later on the smaller Findelengletscher, which has a higher glacier terminus elevation. This leads to higher SCAFs until mid-August. Towards the end of the ablation season, the SCAF is similar for the two glaciers (Fig. 7).
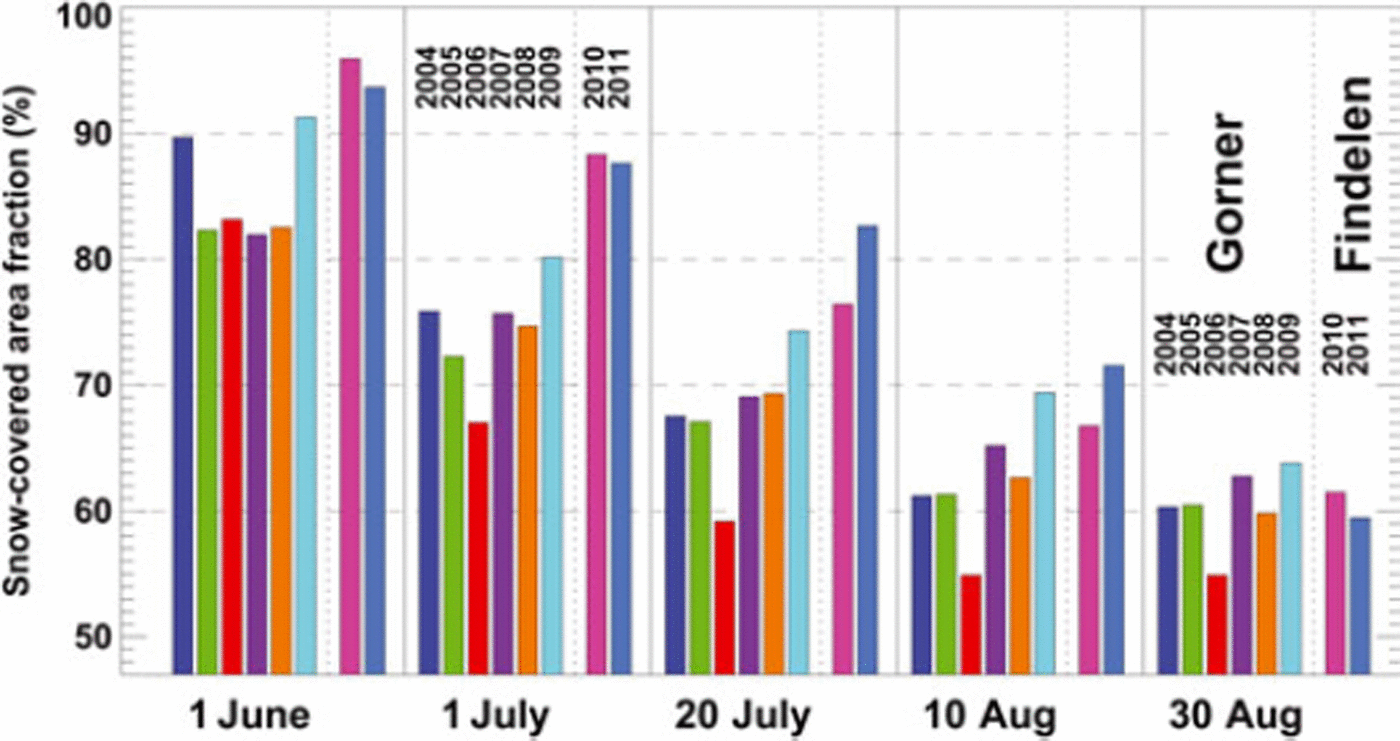
Fig. 7. SCAF at given dates for Gornergletscher (2004–09) and Findelengletscher (2010–11).
Glacier-wide mass balance of Findelengletscher for the 2010 and 2011 ablation seasons is derived from 11 and 16 oblique photographs, respectively, from the automatic camera on Unterrothorn. We apply the methodology given in Figure 5. Computed glacier-wide mass balances for the dates of the first and the last evaluated photographs are compared to seasonal mass balances determined using the glaciological method and the 2009–10 geodetic ice volume change (Fig. 8). For both years, we find an agreement within 0.10 m w.e. with observed winter balance as well as annual balance. In order to assess the quality of short-term mass-balance estimates throughout the ablation season, we compare our results with time series of daily mass balance obtained using a detailed model (Reference Huss, Bauder and FunkHuss and others, 2009) that includes the most important processes governing mass-balance distribution and is calibrated to match all available in situ seasonal mass-balance data. The course of modelled mass balance is reproduced by SCAF-based mass-balance estimates (Fig. 8). However, they are up to 0.3 m w.e. too low in June and July of 2011, as precipitation events in spring or summer primarily affect the still snow-covered upper parts of the glacier and therefore cannot be captured by snowline observations. Remotely inferred winter snow accumulation distribution (phase 1) is validated against distributed in situ measurements (Fig. 1), indicating a bias of -0.04 (-0.20) m w.e. in 2010 (2011), and root-mean-square error (rmse) of 0.16 (0.26) m w.e. The altitudinal distribution of accumulation is closely reproduced (rmse <0.1 m w.e. for both years) in the ablation area, i.e. within the range of transient snowlines, but the errors are higher in the accumulation area, where snow accumulation cannot be directly constrained based on our method.
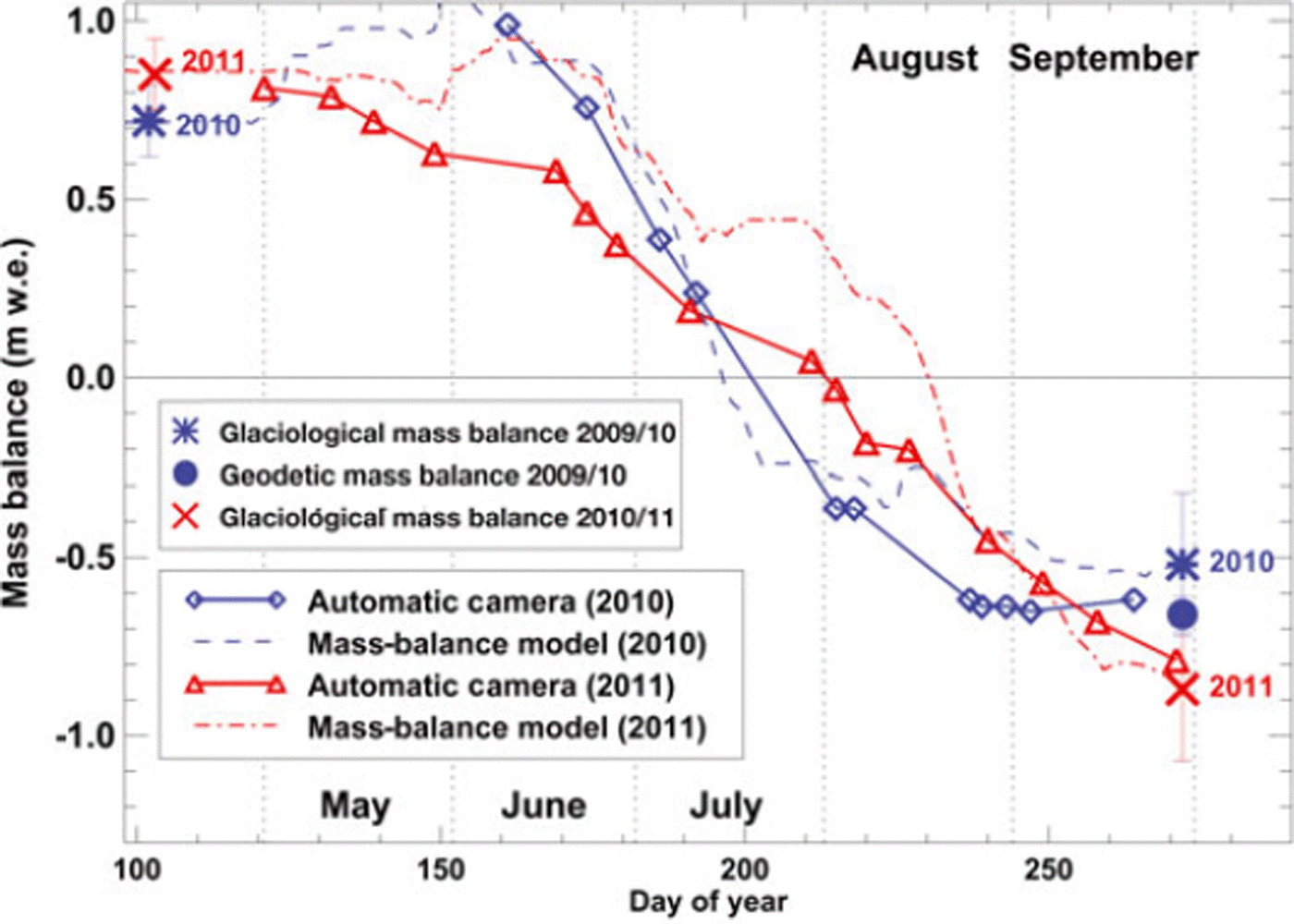
Fig. 8. Glacier-wide mass balance of Findelengletscher in 2010 and 2011 for the dates of evaluated photographs (diamonds, triangles). Large symbols indicate directly observed winter and annual mass balance based on the glaciological method (and include estimated error bars). The geodetic mass change for 2009–10 is shown by a solid dot. Dashed curves refer to simulated mass balance using a detailed model calibrated to the field observations.
Gornergletscher has many inaccessible regions and is too large to be covered by a common glacier-monitoring program. Based on 12–18 camera pictures per year, we estimate mass-balance evolution throughout the 2004–09 ablation seasons (Fig. 9). Unlike the evaluation for Findelen-gletscher, it was not possible to extend the image time series all through the melting season until September. Due to fresh-snow events or unfavourable weather conditions, the latest picture analysed was taken in August in all years. Nevertheless, interannual differences are clearly revealed. The year 2009, for example, showed a much slower snow-cover depletion (Fig. 7) and higher transient mass balance throughout the ablation season compared to other years due to above-average winter precipitation (Fig. 9).
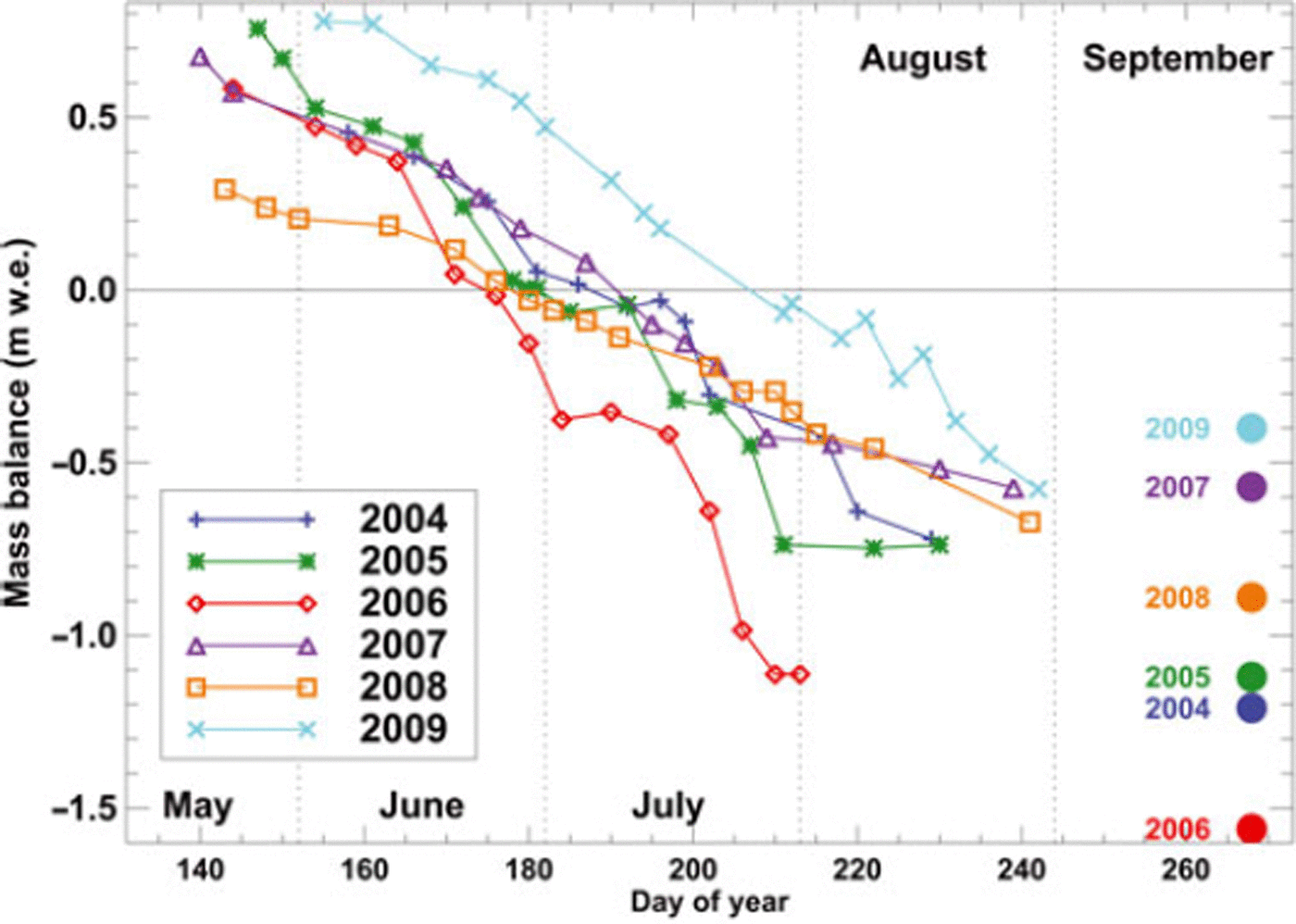
Fig. 9. Glacier-wide mass balance of Gornergletscher in 2004– 09 for the dates of evaluated photographs. Independent modelled annual mass balance based on meteorological data and long-term ice volume change is indicated by dots.
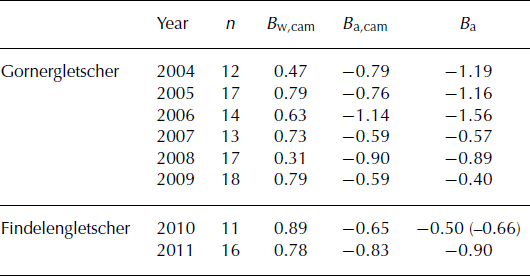
The mass-balance model used to determine the rating curve also allows us to compute seasonal balances for fixed periods of the hydrological year. As the daily model is constrained for each year with the snowline observations between May and August/September, the evaluation of winter mass balance (1 October–30 April) and annual balance (1 October–30 September) is possible. Results are validated against independent datasets (Table 1). SCAF-based mass balance of Gornergletscher is compared to mass-balance model results constrained by long-term volume change (Reference Huss, Hock, Bauder and FunkHuss and others, 2010). Although the evaluated images do not cover the entire ablation season, the agreement of annual mass-balance variability (rmse of 0.30 m w.e.), as well as the 6 year mean mass balance (bias of 0.17 m w.e.) is satisfying (Table 1). It has to be noted, however, that the independent validation datasets are also subject to uncertainties.
Table 1. Inferred glacier-wide winter mass balance, Bw,cam, and annual mass balance, Ba,cam, (m w.e.) using the two-phase framework (Fig. 5) based on n snowline observations for Gornergletscher and Findelengletscher. Ba is the annual mass balance obtained with detailed modelling (Gornergletscher), in situ measurements (Findelengletscher) and a geodetic survey (in parentheses)
Discussion
Although our method yields mass-balance estimates that compare well with independent datasets, considerable uncertainties and restrictions are involved. In general, we do not expect our remote-sensing approach to exhibit an accuracy comparable to in situ measurements of glacier mass balance or repeated geodetic surveys. We rather aim at providing rough values for the short-term mass budget of inaccessible and remote glaciers that can complement existing mass-balance monitoring programs. Our method could also be used to extend mass-balance observations from the date of the last field survey to the end of the hydrological year.
The clear separation of an accumulation and an ablation season is a prerequisite for applying our method. Tropical glaciers, or glaciers in a monsoon-type climate, for example, would require a more complex framework to infer mass balance based on snowline observations.
An important drawback of the proposed approach is its dependence on weather conditions. Only pictures with good visibility for the entire glacier can be analysed. In some years, significantly more than half of the automatic camera images could not be used, because of frequent cloud coverage obstructing the direct camera view of parts of the glacier.
Fresh snow during the summer season is most critical to the application of our method. After a summer snow event, the transient snowline can drop by several hundred metres during 1 day, although there is no significant change in glacier mass. This is what would be implied, however, if the SCAF vs mass-balance rating curve was just applied to all snowline observations (Fig. 6). It is therefore important to only evaluate images for which the delineated snowline refers to exposed winter snow and to discard pictures with a substantial fraction of fresh snow. Distinguishing between the snow types is possible through the albedo contrast of new and old snow, but is not always unambiguous, especially when the snowline is located at high elevations.
Misclassifications of the surface type thus become more likely towards the end of the ablation season. If the snowline rises above the long-term ELA, firn layers are exposed which are difficult to distinguish from snow originating in the previous winter. Furthermore, the viewing angle is unfavourable for the accumulation area in the case of both study sites. The cameras are located approximately at the median glacier elevation and look upward into the accumulation area, which is thus resolved under a small angle.
The automatic classification of the surface type has been shown to yield promising results and allows bare glacier ice to be objectively distinguished from snow at high spatial and temporal resolution (Fig. 3). However, unsupervised classification based on reflectance values is prone to errors, due to fresh snow or shadows cast by clouds, especially at the beginning and end of the ablation season, and needs to be cross-checked using manual snowline detection.
When applying the method proposed in this study, the total estimated uncertainty in the SCAF of 0.5–2.5% can be translated into an error in the inferred mass balance via a typical rating curve (Fig. 6), indicating a potential uncertainty in glacier-wide mass balance of ±0.03–0.08 m w.e. This is within the uncertainty in mass balance based on the glaciological method (e.g. Fig. 8). However, mass balance inferred using SCAF rating curves is also affected by the numerous simplifications and assumptions both in the model input data (meteorological series) and the model itself.
Several sensitivity tests were performed in order to estimate the effect of assumptions in the model set-up on calculated mass balance. In a first experiment, the model was run for Findelengletscher using the climatological series C2 for both phases 1 and 2 (Fig. 5), mimicking the case that no nearby weather station data were available. Compared to the reference results of 2010 and 2011, winter balance varies by ±0.02 and annual balance by ±0.10m w.e. This indicates that the model is relatively robust to the choice of the meteorological input series. Second, the constant degree-day factors for snow and ice were varied within a range of ±25%, and the calculated seasonal mass balances (Findelengletscher) were compared to the reference (Table 2). The sensitivity to variations in the degree-day factors lead to changes in glacier-wide mass balance of ±0.22 m w.e. It is interesting to note that the annual balance is almost insensitive to the chosen value for DDFsnow. The air temperature gradient has a smaller effect on calculated mass balance, and the model is almost insensitive to the solid precipitation threshold (Table 2).
Table 2. Sensitivity of calculated winter balance, Bw, and annual balance, Ba, of Findelengletscher to selected model parameters. Degree-day factors, DDF, for snow and ice were varied by ±25%, the air temperature gradient, dT/dz, by ±1•C km- 1 , and the threshold temperature between solid and liquid precipitation, Tthr, by ±0.5•C. All values are given in m w.e. and represent averages for the years 2010 and 2011
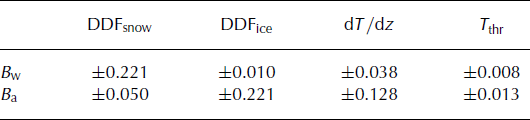
Using a physically based mass-balance model could reduce these uncertainties, but the larger number of input data requirements precludes the application of our method to arbitrary glaciers and undermines the simplicity of the approach. Tests using a distributed energy-balance model including solar radiation and spatial accumulation distribution (Reference Machguth, Paul, Hoelzle and HaeberliMachguth and others, 2006b) did not yield better results than our simple degree-day model.
In this study, we have tested our approach to remotely determining glacier mass balance using terrestrial oblique images provided by automatic cameras. The photographic approach is particularly suited for smaller glaciers for which a high spatial resolution of the transient snowline mapping is required. For larger glaciers, however, repeated satellite imagery could be used to obtain time series of SCAF over the summer season. Several studies have demonstrated the power of spaceborne observation for mapping glacier properties (Reference Konig, Winther and IsakssonKonig and others, 2001, and references therein). Distributed surface albedo of alpine glaciers (e.g. Reference Dumont, Durand, Arnaud and SixDumont and others, 2012a) and mass-balance series at annual resolution have been derived using satellite imagery (Reference Rabatel, Dedieu, Thibert, Letreguilly and VincentRabatel and others, 2008; Reference DumontDumont and others, 2012b). The viewing angle of air- and spaceborne images is more favourable than that of oblique photography, and large samples of glaciers can be covered. For example, the MODIS (Moderate Resolution Imaging Spectroradiometer) mission provides repeated imagery of the Earth surface at high temporal and spatial resolution. These data have been applied to infer glacier surface properties in a number of studies (e.g. Reference Lopez, Sirguey, Arnaud, Pouyaud and ChevallierLopez and others, 2008; Reference DumontDumont and others, 2012b) and could be directly used in our methodology. Thus, there is considerable potential for the proposed approach for estimating sub-seasonal mass balance of inaccessible glaciers in remote mountain ranges based on repeated satellite scenes.
Conclusion
By combining repeated glacier photography throughout the ablation season with simple modelling we compute glacier-wide mass balance at sub-seasonal resolution using remotely acquired information. We have presented a methodology that allows the temporally continuous monitoring of mass balance for large, remote or inaccessible glaciers without requiring in situ measurements. The new approach was tested using hourly to daily pictures from automatic cameras that overlook two valley glaciers in the Swiss Alps covering 8 years in total. Although calculated mass balance is expected to have a lower accuracy than the direct glaciological or the geodetic method, an agreement of 0.1–0.3 m w.e. with independent mass-balance datasets was found both at the annual and the seasonal scale. This indicates the potential of our method for a possible future extension of the mass-balance monitoring network to additional glaciers, based purely on remote-sensing data. For example, the proposed methodology currently supports the re-establishment of long-term glacier monitoring in the Pamirs, Central Asia (Reference HoelzleHoelzle and others, 2012). The determination of glacier-wide mass balance at high temporal resolution is possible based on oblique terrestrial photography, as well as on air- and spaceborne observations, and could therefore also be applied at larger spatial scales. This might contribute to improved estimates of the glacier mass balance in mountain ranges with scarce observations.
Acknowledgements
We thank J. Corripio for providing the software used for georeferencing oblique photographs, D. Sciboz for technical support, H. Boesch for evaluating the photogrammetric DEM for Gornergletscher and P. Joerg for preparing the lidar DEMs for Findelengletscher (supported by the Swiss energy utility Axpo). We thank A. Linsbauer and H. Machguth for contributing to the mass-balance measurements on Findelengletscher. Meteorological data were provided by MeteoSwiss. Constructive comments by two anonymous reviewers and the Scientific Editor E. Berthier were helpful in finalizing the manuscript.












