Introduction
Ocean surface waves that penetrate into the ice-covered ocean force the ice floes there to surge back and forth. The surge motion is most significant over the first ∼10 km in from the ice edge, where the waves have not been damped significantly by the ice cover, and where the average floe size is relatively small, due to wave-induced ice fracture.
Surge motions cause floes to collide if the amplitude of the surge motion is of the order of the floe separations, and if motions of adjacent floes are sufficiently out of phase. Collisions transfer momentum through the ice cover, thus affecting its large-scale rheology (Reference Shen, Hibler and LepparantaShen and others, 1987; Reference FelthamFeltham, 2005). Floe edges are also eroded by coilisions (Reference McKenna, Crocker, Paren and WadhamsMcKenna and Crocker, 1990). In addition, collisions can result in floes rafting on top of one another.
In order to model wave-induced floe/floe interactions accurately, it is first necessary to accurately model wave-induced surge motions. Here we present a theoretical model and a laboratory experimental model of surge motions of an ice floe, in which the floe is modelled as a thin floating disc. The theoretical model is based on a modified version of Morrison's equation, which includes a force due to the slope of the wave field. Morrison's equation is a semi-empirical model, which assumes that the body (here disc/floe) does not affect the surrounding wave field, i.e. it is small in relation to the wavelength.
We use the experimental model to validate the theoretical model, and to establish its range of validity for a thin floating disc. The modified version of Morrison's equation was developed by Reference Rumer and WakeRumer and others (1979) and Reference Marchenko and byMarchenko (1999) for the ice-floe problem. We refer to this model as the Rumer model. Reference ShenShen and Ackley (1991) analysed the Rumer model as part of their investigation into the drift of pancake ice. Reference Shen and ZhongShen and Zhong (2001) derived an analytic approximate solution for the Rumer model. Reference Grotmaack RandGrotmaack and Meylan (2006) proved that all solutions of the Rumer model tend to the same steady-state solution (for moderate wave steepnesses))
A series of laboratory experiments, closely related to ours, have been reported by I Reference Huang and HuangHuang and others (2011) and Reference HuangHuang and Law (2013). The experiments were designed to investigate drift of a thin floating body in waves. However, experimental measurement of drift in a wave tank is extremely challenging, because Stokes drift induces a large-scale circulatory motion in the tank. This can corrupt the drift and lead to anomalous results, with drift velocities significantly exceeding Stokes drift.
In the following sections we present the Rumer model, and describe our experimental work and data analysis. A comparison of surge motions predicted by the theoretical and experimental models is then presented. We find that the Rumer model is accurate when wavelengths are greater than twice the floe diameter. I leave and pitch motions of the disc measured during the experiments are also presented.
Theoretical Model
Reference Rumer and WakeRumer and others (1979) and Reference Marchenko and byMarchenko (1999) developed models of horizontal motions of an ice floe due to waves, assuming that the floe is much smaller than the wavelength. We use a combination of the models of Reference Rumer and WakeRumer and others (1979) and Reference Marchenko and byMarchenko (1999), derived by Reference Grotmaack RandGrotmaack and Meylan (2006), which assumes low wave steepness. We restrict our investigation here to monochromatic waves.
Wave forcing on small floating bodies
The force acting on a small body (in relation to the wavelength) is decomposed into two components: (1) a sliding force due to gravity and (2) a drag force between the water and the body.
Gravity
The sliding force due to gravity, F g, is given by
where η is the profile of the water surface, x(t) is the horizontal location of the body, m is its mass and g ft* 9.81 ms-2 is gravitational acceleration.
For a monochromatic wave, of height H, wavenumber k and frequency f, the wave profile at time t is
The slope of the surface profile is therefore
Drag
Drag force, F d, is caused by friction between the body and the water, and is expressed as
Here pw is the mass density of the fluid, W is the reference (wetted surface) area, Cd is the drag coefficient, and Vw and V are horizontal velocities of a water particle at the surface of the fluid and the body, respectivey. From Eqn (2) the velocity of a water particle is
Inertia
The inertial force, Fi, is
Here, Cm is the so-called added mass coefficient; it accounss for 'virtual mass' due to fluid around the body.
Rumer model
We derive the nonlinear ordinary differential equation (ODE)
for the velocity of the body, V, by combining Eqns (1), (3) and (5). Substituting Eqns (2) and (4) into the ODE gives

The added mass and drag coefficients, C„, and Cd, are, generaly,, determined experimentally, and are considered known. By solving the above ODE, we are able to predict the horizontal veloctty of the body for an incident wave of prescribed height, wavenumber and frequency.
If we introduce a variable θ = kx-2πft the ODE reduces to the autonomous system

and
This system always has a stable periodic solution. Further, outside the very steep wave regime, the periodic solution is the only attractor in the system, i.e. all solutions tend to the periodic solution, regardless of the initial conditions. However, the period of the periodic: solution does not exactly match the period of the wave, due to drift. The amplitude in surge is found by integrating the velocity over a single period.
Wave Tank Experiments
An experimental model of wave-induced surge motion of a floe was implemented in the model test basin (MTS) of the Australian Maritime College, Launceston, Tasmania. The MTS is 35 m long and 12 m wide.
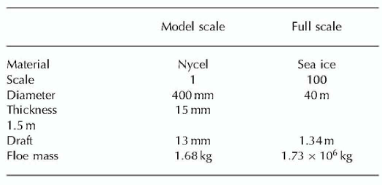
The floe was modelled by a thin Nycel plastic disc, of 400 mm diameter and 15 mm thickness. At a scale of 1.100 this models an ice floe of 40 m diameter and 1.5 m thickness. Nycel is a closed-cell expanded-foam rigid PVC sheet with a thin hard plastic coating. Table 1 provides a summary of parameters for the floe model.
Table 1. Floe parameters
Tests were conducted for the floe with and without a polystyrene edge barrier (50 mm high and 25 mm thick). This restricts overwash, i.e. the wave running over the top of the floe. Figure 1 shows floes with and without an edge barrier.

Fig. 1. Model floes. With edge barrier (foreground) and without edge barrier (background).
Overwash is not yet included in theoretical models. We therefore only present results from tests conducted with the barrier. (Overwash has negligible impact on floe motions for large wavelengths, and damps floe motions for smaller wavelengths.)
A mechanical wavemaker was used to generate regular (monochromatic) waves. Wave heights of 10-80 mm and frequencies of 0.5-2 Hz were tested, with corresponding wavelengths ∼0.5 - 5 m. Wave gauges were located 1 m in front of the equllibrium position of the floes, in order to verify the incident wave heights.
The ambient fluid depth w a s 800 mm. The floes were moored to the MTB floor with a 1.6 m long elastic band. A static beach was located at the opposite end of the MTB to the wavemaker, in order to reduce the waves reflected at this boundary. The equilibrium position of the floes was 17.7 m from the beach.
Four spherical polystyrene markers, 30mm in diameter, mounted on lightweight aluminium cylinders, were attached to each floe. The markers and mounts are visible in Figures 1 and 2, and were sufficiently light to have negligible influence on the motion of the floes.

Fig. 2. Model floe during test. Scattered waves are evident.
The location of the markers was measured stereoscopically by the Qualysis motion-tracking system, via a set of infrared cameras. The Qualysis system provides time series of the translational and rotational motion of the floes. The translational motions give the location of the floes with respect to a Cartesian coordinate system, (x, y, z). The origin of the coordinate system is the equilibrium centre of the floe with a barrier. Horizontal translations are described by the (x,y) coordinate, where x denotes the location along the MTB, pointing from the wavemaker to the beach, and y denotes the location across the MTB. Vertical motion,, i.e. heave, are described by the z-coordinate. The rotational motions provide the pitch, roll and yaw motions of the floes.
Data processing
Raw data were first smoothed to eliminate noise, using the MATLAB package function smooth. The lowess local regression method, using weighted linear least squares, was selected along with an appropriate smoothing factor.
The smooth function was also used to decouple the surge and drift motions from the translational signal in the x-direction. For a sufficiently large smoothing factor, the smooth function eliminates the surge oscillations from the signal, and thus returns the drift. The surge motion is then calculated as the difference between the signal and the drift. An example of the decomposition method is shown in Figure 3, where the effect of the mooring, which restricts the drift motion, can also be seen. (The effect of mooring on the surge motion amplitude, howeve,, can be seen to be negligible.)

Fig. 3. Example decomposition of surge and drift motions. Full signal (solid curve), drift (dashed) and surge (dot-dash).
During a given test, the magnitude of surge and drift motions varies with time due to, initially, transients in the first few wavefronts, and, later, interference caused by waves reflected by the beach. We therefore identify a steady-state window, i.e. a time interval beginning after incident wave transients have passed and finishing before reflected waves reach the floe, and analyse the signal in this interval only.
The steady-state window can be calculated analytically using the wave celerity (phase speed). In practice, we use a conservative estimate of the steady-state window. An example of the steady-state window is shown in Figure 4 (with the peaks and troughs of the signal within the window identified). Wave heights are calculated as the differences between consecutive peaks and troughs. A representative amplitude for the motion in the steady-slate window, in this case the heave motion, is calculated as half the mean of the set of calculated heights.

Fig. 4. An example of the steady-state window (solid curve). Circles mark peaks and troughs within the window.
Results
Comparisons of surge amplitudes measured in the experiments and predicted by the Rumer model are shown in Figures 5-8. The surge amplitudes are non-dimensionalized with respect to the incident wave horizontal particle amplitude, '4 tanh (kH). The wave heights used are those measured by the wave gauge in front of the floe. Therefore, heights referred to hereafter are the target heights. The non-dimensional surge amplitudes are presented as functions of wavelength, non-dimensionalized with respect to floe diameter. The different figures show results for different added mass coefficients, Cm, and wave heights, H, in the Rumer mode. Four different values of the drag coefficient are considered for each added mass and wave height combination.

Fig. 5. Comparison of non-dimensional surge amplitude, as a function of non-dimensional wavelength, predicted by the Rumer model (curves) and experimental data (symbols). The Rumer model uses added mass Cm = 0.1, wave height H = 10 mm, and drag coefficient Cd = 0 (solid curve), 0.005 (dashed), 0.1 (dot-dash) and 0.5 (dotted). Experimental data are taken from tests with wave heights H = 10mm (o), 20mm (x), 30mm (+), 40mm (*), 50mm (⋄), 60 mm (∇), 70 mm (Δ) and 80 mm (◃).

Fig. 6. Same as Figure 5, but for H = 40 mm.

Fig. 7. Same as Figure 5, but for H = 40 mm and Cm = 0.

Fig. 8. Same as Figure 5, but for H = 40 mm and Cm = 0.2.
The experimental data are identical in the different figures. The experimental data are grouped according to incident wave height. Very little spread is seen with respect to wave height. For the majority of the non-dimensional wavelengths considered, the experimental surge is approximately equal to the incident wave amplitude. For large wavelengths, the floe behaves like a particle on the surface, modified by the added mass.
A regime change occurs when the wavelength is approximately equal to two floe diameters. For wavelengths less than this transition length, the surge amplitude rapidly decreases with decreasing wavelength. For the smallest wavelength considered, which is approximately equal to the floe diameter, the surge amplitude is approximately one-fifth of the incident amplitude.
The surge amplitudes given by the Rumer model are insensitive to the value of the drag coefficient, Cd, for the majority of the non-dimensional wavelengths considered. (If required, the drag coefficient can be measured experimentally by a towing test.) Surge is also insensitive to wave height. Increasing/decreasing the added mass decreases/increases the surge motion, which can be understood intutively.
Surge amplitudes predicted by the Rumer model agree with the experimental data for wavelengths greater than approximately two floe diameters - the point at which a regime shift occurs in the experimental data. The added mass coefficient Cm = 0.1 provides the best agreement between the Rumer model and the experimental data (for wavelengths greater than two floe diameters). This value of Cm agrees with values found in the literature (e.g. Reference ShenShen and Ackley (1991) use a value of Cm = 0.15).
The non-dimensional heave and pitch motions measured in the experiments are shown in Figures 9 and 10, respectively. (The Rumer model assumes that the floe follows the wave surface, i.e. it assumes heave and pitch amplitudes equal to the incident wave amplitude.)
A transition in the motios is again evident at a wavelength approximately equal to two floe diameters.

Fig. 9. Experimental data for heave motion. The results are labelled by approximate wave height, as in Figure 5.

Fig. 10. Experimental data for pitch motion. The results are labelled by approximate wave height, as in Figure 5.
Summary and Discussion
Theoretical and experimental models of surge motions of an ice floe, induced by regular waves, have been presented. The theoretical Rumer model is based on a modified version of Morrison's equation. The Rumer model assumes that the floe does not disturb the wave field. Surge motions result from the force of gravity in conjunction with the slope of the waves, and drag force on the wetted surface of the floe.
The experimental model used a thin plastic disc to model the floe. The model was implemented in a wave basin at scale 1:100. The rigid-body motions of the floe were measured by a motion-tracking system. The raw time-series data were processed to obtain the steady-state surge amplitude of the floe, for different wave heights and frequencies/wavelengths.
The surge amplitude, non-dimensionalized with respect to the incident wave amplitude, was presented as a function of wavelength, non-dimensionalized with respect to floe diameter. The experimental data displayed a regime change from a rapid increase in non-dimensional surge with increasing non-dimensional wavelength, to a weak increase. The transition between regimes occurred at a wavelength approximately twice as large as the floe diameter. The regime change was also evident for heave and pitch motions in the experiments.
The Rumer model was able to predict surge motions accurately for wavelengths larger than the transition wavelength. An alternative theoretical model is clearly required for wavelengths less than two floe diameters. In this regime, it is likely that a model based on linear potential flow theory will provide more accurate predictions of floe motions. Potential flow theory includes modifications to the wave field surrounding the floe due to wave scattering.
Acknowledgements
Experiments were funded by the Australian Maritime College. L.G.B. acknowledges funding support from the Australian Research Council (DE13010557.). M.H.M. and L.G.B. acknowledge funding support from the Australian Antarctic Science Grant Program (Project 4123..












