1. Introduction
Glaciers and ice caps were the main contributors to sea-level rise during the 20th century (Reference GregoryGregory and others, 2013) and also in the 21st century their contribution is projected to be large (Reference ChurchChurch and others, 2013). However, the mass loss of glaciers in the present century results not only from the additional warming, but is also a consequence of glacier response to the 20th-century warming (Reference Bahr, Dyurgerov and MeierBahr and others, 2009; Reference Marzeion, Jarosch and GregoryMarzeion and others, 2014). This is a consequence of the response time, because a change in mass balance takes time to translate into a length and volume change (Reference Cuffey and PatersonCuffey and Paterson, 2010). A better insight into the response time of glaciers is therefore crucial to improve future glacier projections (Reference Zuo and OerlemansZuo and Oerlemans, 1997).
It is, however, difficult to estimate the climate–geometry imbalance and response time of a glacier from observations, as the forcing that glaciers are subjected to changes continuously. Therefore our knowledge of response times relies mainly on analytical methods, conceptual models or numerical experiments with idealized glacier set-ups (e.g. Reference Jóhannesson, Raymond, Waddington and OerlemansJóhannesson and others, 1989; Reference OerlemansOerlemans, 1989; Reference Harrison, Elsberg, Echelmeyer and KrimmelHarrison and others, 2001; Reference Leysinger Vieli and GudmundssonLeysinger Vieli and Gudmundsson, 2004; Reference Raper and BraithwaiteRaper and Braithwaite, 2009). Explicit modelling studies on individual real glaciers are needed to complement these approaches (Reference OerlemansOerlemans and others, 1998). With careful calibration against past changes such studies can provide valuable information about the glacier’s present-day state. Interpreting the response time for a real glacier is more complicated than in a conceptual set-up, but is needed to assess the value of the different analytical methods and to better unravel the various processes contributing to the response time of a particular glacier. This is recognized in the analysis of glacier response time by Reference Raper and BraithwaiteRaper and Braithwaite (2009), who state that more detailed dynamic flow modelling of individual glaciers is needed for a better understanding. To date, research on the response time of individual glaciers has been limited and based on simple flow models (e.g. Reference OerlemansOerlemans, 1988; Reference Huybrechts, De Nooze, Decleir and OerlemansHuybrechts and others, 1989; Reference Adhikari, Marshall and HuybrechtsAdhikari and others, 2011). Only a few glacier studies have been performed with higher-order (HO) or full-Stokes (FS) three-dimensional (3-D) flow models (e.g. Reference Jouvet, Huss, Blatter, Picasso and RappazJouvet and others, 2009, Reference Jouvet, Huss, Funk and Blatter2011), but these do not focus on the glacier response time.
Here we investigate the climate–geometry imbalance and response time of the well-monitored Morteratsch glacier, Switzerland, by coupling a two-dimensional (2-D) surface mass-balance model to a 3-D HO ice flow model at a high spatial resolution. The modelling relies on an extensive observational dataset and on ice flow and mass-balance models that are calibrated and validated against different sources. This unique set-up allows us to analyse the response time of an alpine glacier in a realistic setting and look at the different factors that influence it, with a particular focus on those that are not taken into account in analytical methods and conceptual models. We start by analysing the present-day (Section 3) and past (Section 4) climate–geometry imbalance. Subsequently, we focus on response time and the effect of the magnitude (Section 5.1) and spatial distribution (Section 5.2) of the forcing, the effects of which hitherto have not been investigated. Response times from our numerical simulations are compared with analytical methods (Section 5.3), and the influence of glacier size is also examined (Section 6). Finally, we discuss the applicability of volume–area scaling (Section 7), suggest how the glacier slope can be incorporated, and analyse the impact of the climate–geometry imbalance on this relationship.
2. Location, Previous Work and Experimental Set-Up
The Morteratsch glacier complex is situated in the Engadine, southeastern Switzerland (Fig. 1), and consists of the main Vadret da Morteratsch and its tributary, Vadret Pers. At present (2012), the glacier has a length of 6.3 km, an area of ~16.0 km2 and spans an elevation range between 2100 and 4000 m. Over the last 13 years our research group has collected an elaborate dataset on annual mass balance, ice thickness and surface velocity. These data were used to calibrate a 2-D surface energy-balance model (Reference Nemec, Huybrechts, Rybak and OerlemansNemec and others, 2009), to reconstruct the ice thickness and calibrate a 3-D ice flow model (Reference Zekollari, Huybrechts, Fürst, Rybak and EisenZekollari and others, 2013), and to simulate the transient evolution of Morteratsch glacier between 1864 and 2100 (Reference Zekollari, Fürst and HuybrechtsZekollari and others, 2014). In the latter study, a time-dependent mass-balance correction between 0 and 0.5mw.e. a–1 was required between 1864 and 1960 in order to correctly reproduce the observed retreat (Glaciological Reports, 1881–2009), while the evolution from 1960 to 2010 was validated against topographic and volume changes derived from digital elevation models (Reference Zekollari, Fürst and HuybrechtsZekollari and others, 2014).

Fig. 1. (a) 2012 transient glacier geometry. The glacier complex consists of Vadret da Morteratsch (M) and Vadret Pers (P). The highest surrounding peaks are Piz Bernina (PB; 4049 m), Piz Zupo (PZ; 3996 m) and Piz Palü (PP; 3905 m). (b) Glacier geometry in equilibrium with the 1983–2012 climate; (c) steady-state glacier with the same volume as the glacier in 2012; and (d) a steady-state glacier with the same length as the glacier in 2012. The red dot on the map of Switzerland indicates the location of Vadret da Morteratsch.
The experiments discussed here to investigate the glacier’s response time use the same model set-up and flow parameters as in Reference Zekollari, Fürst and HuybrechtsZekollari and others (2014). We use a HO glacier flow model of the Blatter/Pattyn type (Reference BlatterBlatter, 1995; Reference PattynPattyn, 2003), with an efficient and more stable finitedifference implementation of the governing equations (Reference Fürst, Rybak, Goelzer, De Smedt, De Groen and HuybrechtsFürst and others, 2011). The horizontal resolution is 25 m and there are 21 layers in the vertical. The internal deformation is described by Nye’s generalization of Glen’s flow law (Reference GlenGlen, 1955; Reference NyeNye, 1957). For basal sliding, a Weertman-type sliding law (Reference WeertmanWeertman, 1964) is used in which the basal drag corresponds to a HO approximation of all basal resistive stresses (following Reference Van der Veen and WhillansVan der Veen and Whillans, 1989). The flow model is coupled to the simple energy-balance model of Reference Nemec, Huybrechts, Rybak and OerlemansNemec and others (2009), which accounts for the shading effect of surrounding mountains and seasonal changes in albedo. The present-day ice-free patches above 3000 m are explicitly kept ice-free in all simulations, as we know from historical evidence that since the Little Ice Age (LIA) these have never been covered with ice.
In general, the asymptotic approach to a steady state can be described using relatively simple models (Reference Raymond, Waddington and JøhannessonRaymond and others, 1990), except for small mass-balance perturbations, where approaches based on the shallow-ice approximation (SIA) can be problematic (Reference GreuellGreuell, 1992). Furthermore the presence of basal motion leads to differences in response time between SIA models and more complex flow models, including longitudinal and transverse stress gradients (Reference GudmundssonGudmundsson, 2003). This justifies the use of a HO ice flow model in the current study.
3. Present-Day Steady State
3.1. Forcing with present-day climate
Morteratsch glacier is strongly out of equilibrium with the climate in which it is situated. Under the 1983–2012 average climate, a mean specific mass balance of –0.55mw.e. a–1 is obtained for the 2012 transient glacier geometry (Fig. 1a). Using these climatic conditions as an input for the mass-balance model and coupling it to the dynamically calibrated ice flow model leads to a strong retreat of the glacier until a new equilibrium with the imposed climate is reached (Fig. 1b). As the model was extensively tuned and validated for the past, we interpret this retreat as an adaptation to the climate–geometry imbalance and not as an artefact of modelling uncertainties (e.g. uncertainty in bed or flow parameters). The glacier thinning occurs mainly at low elevations, where the glacier adapts to the reduced ice flux divergence similar to other glaciers (Reference Berthier and VincentBerthier and Vincent, 2012). This leads to a frontal retreat of 1250m for Vadret da Morteratsch, while its main tributary, Vadret Pers, disconnects and retreats 500m (Fig. 1b). During this retreat the mean specific mass balance evolves to 0mw.e. a–1 as expected, which takes ~100 years (red curve in Fig. 2a). The accumulation–area ratio (AAR) increases from 50% to 58%, mainly because the glacier has lost part of its tongue area with the highest ablation.
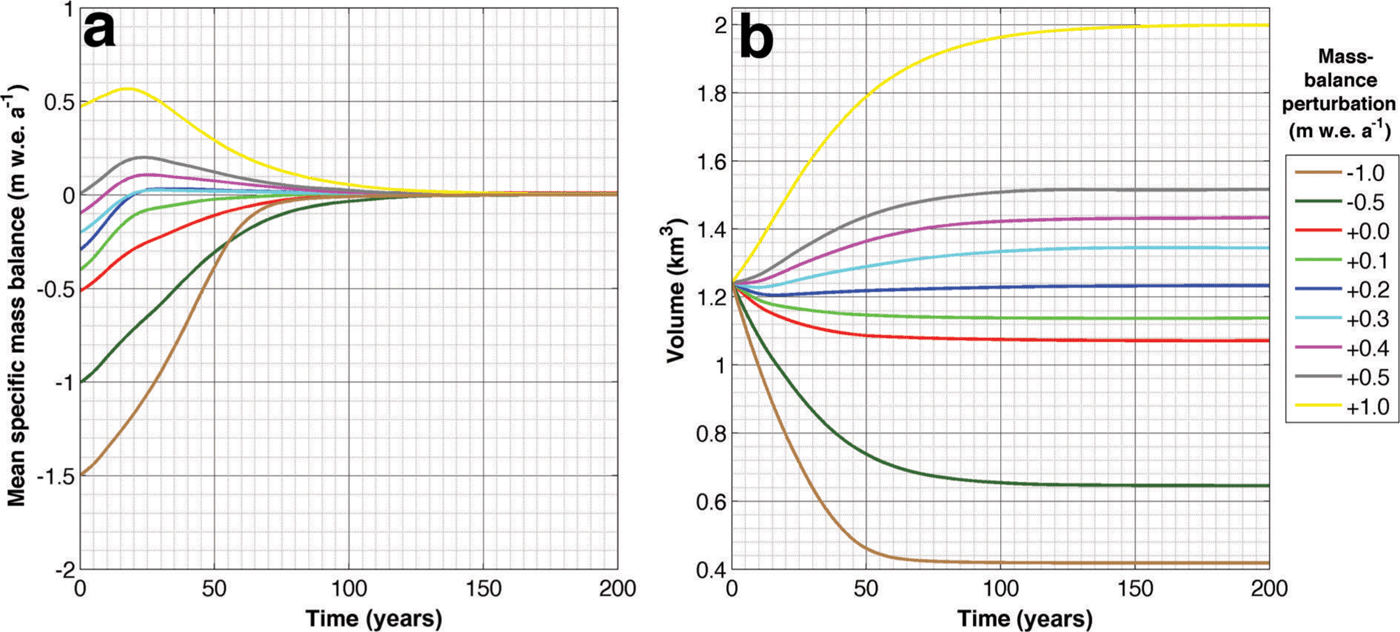
Fig. 2. Evolution of 10 year running mean specific mass balance (a) and volume over the glacier (b) for different mass-balance perturbations versus the 1983–2012 climate. Initial condition of the simulation is the 2012 geometry from a transient simulation.
This retreat may be influenced by other factors, such as changes in debris cover and albedo. A debris layer of considerable size has an insulating effect on the glacier surface and leads to reduced ablation. In the likely case of a future extension and thickening of this debris layer, the volume loss and glacier retreat would be attenuated (Reference Jouvet, Huss, Funk and BlatterJouvet and others, 2011). On the other hand the albedo of exposed ice in the summer is known to decrease due to accumulation of dust from exposed side moraines (Reference Oerlemans, Giesen and Van den BroekeOerlemans and others, 2009). Lowering the ice albedo to 0.25 (from 0.37 in our set-up) leads to an additional frontal retreat of 500 m, and the volume loss increases to 90%, while with an ice albedo of 0.15 the glacier retreats an additional 675 m and the volume loss increases to 128%.
3.2. Glacier with present-day length and volume
In order to obtain steady-state geometries with the 2012 length and volume an ensemble of runs is launched with different mass-balance perturbations compared with the 1983–2012 climatology (Fig. 2). For a steady-state glacier with the 2012 volume (1.24 km3) a mass-balance perturbation of +0.2mw.e. a–1 on top of the 1983–2012 average climatology mass-balance field is required (Fig. 2b). This corresponds to a precipitation increase of 10%, or alternatively, a temperature decrease of 0.4°C. Only a small positive perturbation is needed, as little ice volume is present in the glacier’s frontal region, where the imbalance is mainly located. The steady-state glacier configuration with the 2012 volume (Fig. 1c) is almost 1 km shorter than the 2012 transient glacier (Fig. 1a), mainly because the tongue of the steady-state glacier is thicker than for the retreating transient glacier.
To obtain a steady-state glacier with the 2012 length, on the other hand, a mass-balance perturbation of about +0.5mw.e. a–1 is required (Fig. 3), close to the value needed to neutralize the current mass imbalance of –0.55mw.e. a–1. This corresponds to 20–25% higher precipitation or, alternatively, to a temperature change of ~–0.9°C compared with the 1983–2012 climate. The resulting glacier (Fig. 1d) has a thicker frontal region than the 2012 transient glacier, which translates into a 22% larger volume (Fig. 2b). This ‘lengthpreservation’ experiment illustrates the slow response of the system, as the glacier initially continues to retreat a maximum of 750 m, despite the applied positive massbalance perturbation (Fig. 3). The retreat lasts for almost 25 years, until the effect of the higher flux from upstream becomes dominant and allows the glacier to advance again to its present-day position. This advance results from the increase in mass balance applied at the beginning of the experiment (Fig. 2b). The glacier’s slow response is also clear from the evolution of its area, which is almost identical under the constant 1983–2012 climate, and for the ‘lengthpreservation’ experiment for the first 20 years (Fig. 3). This long reaction time, also referred to as initial terminus response time, fits the characteristics of the glacier at this extent (Reference Pelto and HedlundPelto and Hedlund, 2001).

Fig. 3. Evolution of area and glacier length over time while maintaining the 1983–2012 climate (red) and for a mass-balance perturbation of +0.5mw.e. a–1 (grey) compared with this period. Initial condition of the simulation is the modelled transient state of the glacier in 2012.
The preservation experiments with a strong forcing (–1.0, –0.5, +0.5 and +1.0mw.e. a–1) display an exponential volume evolution (Fig. 2b). This evolution is therefore best characterized by its e-folding timescale in which the response time (T
e) corresponds to the time a glacier needs to complete a fraction ![]() (i.e. 63.2%) of its final volume change. This formulation of the response time arises naturally from solving a differential equation for glacier volume after applying a stepwise mass-balance perturbation from an initial steady state. However, the latter is not the case here, which has several implications that are discussed in Section 5.1. The volume response times obtained from the preservation experiments vary around 30 years and are shorter for a glacier retreat (24.5 and 30.1 years for –1.0 and –0.5mw.e. a–1 forcing, respectively) than for an advance (43.8 and 41.3 years for +0.5 and +1.0mw.e. a–1 forcing respectively).
(i.e. 63.2%) of its final volume change. This formulation of the response time arises naturally from solving a differential equation for glacier volume after applying a stepwise mass-balance perturbation from an initial steady state. However, the latter is not the case here, which has several implications that are discussed in Section 5.1. The volume response times obtained from the preservation experiments vary around 30 years and are shorter for a glacier retreat (24.5 and 30.1 years for –1.0 and –0.5mw.e. a–1 forcing, respectively) than for an advance (43.8 and 41.3 years for +0.5 and +1.0mw.e. a–1 forcing respectively).
4. Quantifying the Climate–Geometry Disequilibrium in Time
Since the LIA, Morteratsch glacier has been retreating continuously, reducing its length by ~30% (Glaciological Reports, 1881–2009; Reference Maisch, Burga and FitzeMaisch and others, 1999). The disequilibrium between the climate and glacier geometry has changed over time, but due to the glacier’s response time the disequilibrium cannot be derived directly from the observed length or volume record. The climate–geometry imbalance is investigated here for different periods in the last 50 years by imposing the mean climate of the preceding 10 or 30 years (Fig. 4). This is conducted from 1970 onwards for the 10 year climatology and from 1990 onwards for the 30 year climatology. Such a procedure is not applicable for an earlier time because until 1960 an additional mass-balance bias was required to correctly simulate the historical retreat of the glacier since 1860 (Reference Zekollari, Fürst and HuybrechtsZekollari and others, 2014).
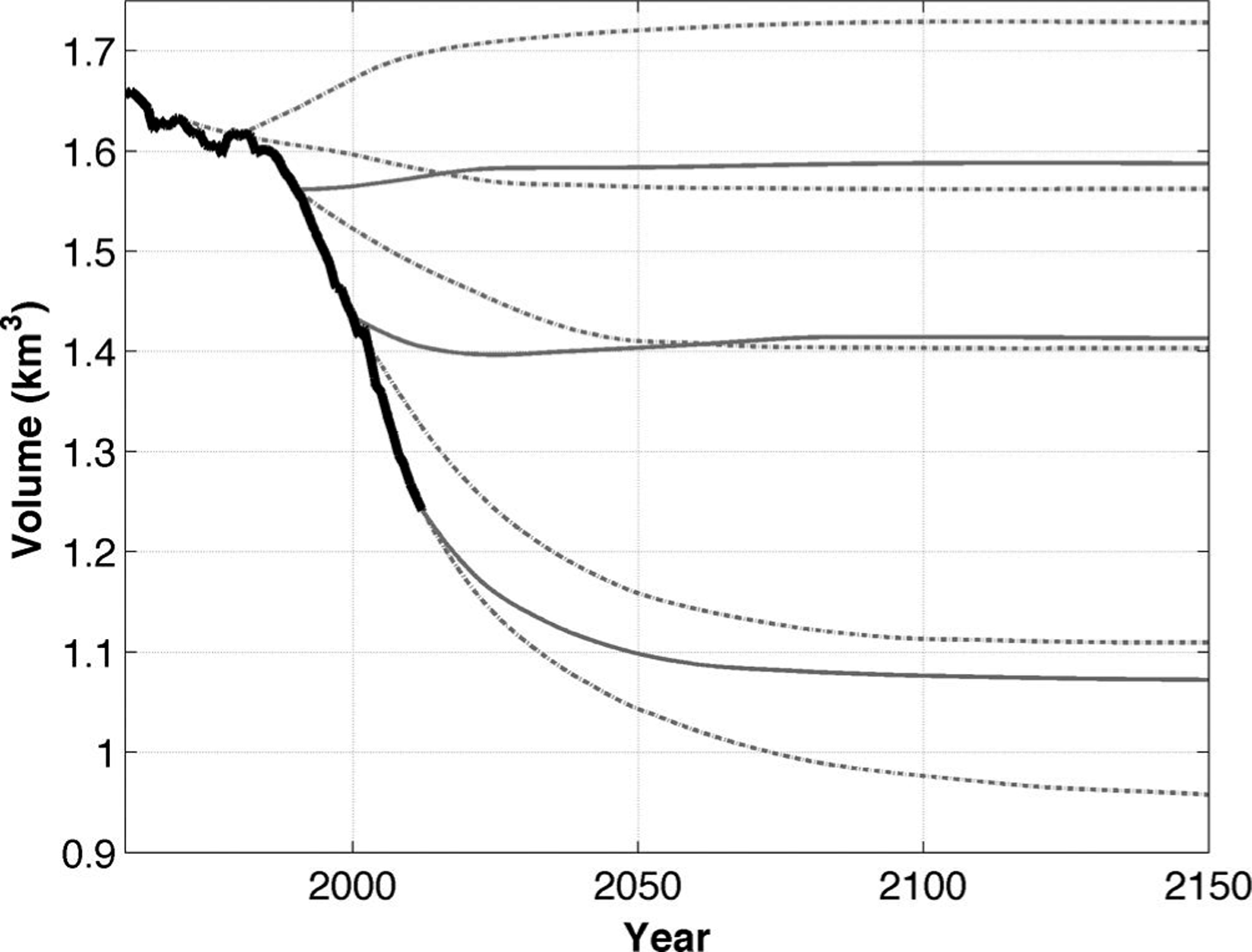
Fig. 4. Evolution of glacier volume when preceding 10 (dashed line) and 30 year (solid line) average climatologies are applied for different moments during the transient evolution. The black line represents the modelled volume evolution between 1960 and 2012 (Reference Zekollari, Fürst and HuybrechtsZekollari and others, 2014).
Over the past half-century, the climate–geometry imbalance has never been larger than at present, since the strongest retreat and volume loss occur for the present-day glacier and climate. Over recent decades the temperature has increased relatively faster than the glacier geometry was able to adapt to the ongoing warming, causing an increased climate–geometry imbalance.
The only time at which the glacier was close to a steady state was in 1990, when the geometry adjusts minimally (0.2% area increase) under the 1961–90 climate and the ice volume remains almost the same (1.6% increase) (Fig. 4). The period from 1965 to 1975 was the coldest of the last 70 years, causing the glacier retreat to be very limited in the second part of the 1980s and leading to the nearly steady-state situation of 1990. The time lag between the colder period from 1965 to 1975 and the decreased glacier retreat suggests that the response time of the glacier must be of the order of a few decades.
5. Glacier Response Time
The experiments discussed so far do not allow ‘clean’ statements to be made about the response time as an initial trend is present. In order to investigate the glacier’s response time, the steady-state glacier with present-day length is now used as an initial state.
5.1. Mass-balance perturbation
The steady-state glacier is forced with uniform mass-balance perturbations between –2.0 and +1.25mw.e. a–1 at an interval of 0.25mw.e. a–1. These perturbations are applied on top of the initial mass-balance field obtained from the 1983–2012 climatology, in addition to a uniform +0.5mw.e. a–1 forcing that is required to obtain an initial glacier with the 2012 length.
5.1.1. Volume response time
Volume response times vary between 21.7 (–2.0mw.e. a–1 forcing) and 42.7 years (+1.25mw.e. a–1 forcing) (Fig. 5). For a limited glacier retreat (forcing between –0.25 and –1.0mw.e. a–1) there is no clear correlation between the magnitude of the forcing and the volume response time, which varies between 31 and 33 years. As the magnitude of the forcing increases, the final volume loss also increases, but so does the rate at which this volume is lost, and both outweigh each other in terms of volume response time.

Fig. 5. Evolution of volume (a) and length (b) for different mass-balance perturbations (from –2.0 to +1.25mw.e. a–1, in intervals of 0.25mw.e. a–1). Initial condition of the simulation is a steady state with the same length as the present-day glacier, obtained by applying a +0.5mw.e. a–1 mass-balance bias on top of the average 1983–2012 climate. This bias is maintained during the simulations. The red and blue dots mark the position where the volume and length response times are reached respectively. (c) Volume and length response time for different mass-balance perturbations. For the three most negative perturbations the length response time could not be determined, as the glacier disintegrates into separate ice patches during its retreat.
For strong negative perturbations (from –1.25 to –2.0mw.e. a–1) the present-day ablation area, which contains most of the glacier’s ice volume, is lost. For all these experiments there is not much difference in the final volume obtained (Fig. 5a). However, the volume loss rate increases with the magnitude of the perturbation, meaning that the volume response time decreases as the magnitude of the perturbation increases. For the strong negative perturbations it is the specific volume–elevation distribution of Morteratsch glacier that determines its response time.
The relationship between the magnitude of the mass-balance perturbation and the response time is different for an advancing glacier. As the magnitude of the forcing increases, the final volume increases relatively faster than the rate of the volume increase (Fig. 5a), and this leads to longer response times. The strong volume increase results from a glacier advance in the very flat glacier forefield, where ice thickness can be up to 200–250 m, similar to the situation at the end of the LIA.
For large perturbations, volume response times derived from the steady-state experiments appear to be close to those derived from the 2012 transient geometry as initial condition (Section 3.2). For the steady-state geometry experiments, the volume response time is 22 years for the –2.0mw.e. a–1 forcing (vs 20 years for the present-day geometry), 31 years for the –1.0mw.e. a–1 forcing (vs 25 years), 34 years for the –0.5mw.e. a–1 forcing (vs 30 years), 36 years for the +0.5mw.e. a–1 forcing (vs 44 years) and 42 years for the +1.0mw.e. a–1 forcing (vs 41 years). Owing to its thinner tongue, the present-day glacier retreat will be faster than for an initial steady state, and its advance slower. Since only little ice volume is present in the frontal region of the present-day glacier, this has an opposite effect on the glacier’s response time. For a retreat, the final volume change is smaller for the present-day glacier compared with a steady-state glacier of the same length. The two effects partly outweigh each other, and as a result the volume response times derived directly from the transient glacier geometry are close to those derived from a steady-state glacier of the same length. It is interesting to note that the response time of 32 years derived from the evolution of the mean specific mass balance for the present-day glacier geometry under fixed present-day climate conditions (no-warming experiment) (Reference Zekollari, Fürst and HuybrechtsZekollari and others, 2014) is close to the 34 years obtained here from the steady-state experiments. These findings suggest that for large perturbations the response time of a retreating glacier can be derived directly from its transient geometry.
5.1.2. Length response time
The length response time is less well correlated with the magnitude of the perturbation and varies between 47 and 55 years (Fig. 5). The remarkably long length response time for the –0.25mw.e. a–1 experiment relates to the flat bed in front of the glacier, due to which a strong frontal retreat of 900m occurs. Length response times (Fig. 5b) are in all cases greater than the volume response times, as the glacier volume reacts immediately (Fig. 5a), while for the length a certain amount of time is needed, the ‘initial terminus response time’ (Reference Pelto and HedlundPelto and Hedlund, 2001). The ratio between the length and volume response time varies from 1.29 (+1.25mw.e. a–1 forcing) to 1.65 (–1.25mw.e. a–1 forcing). This is in line with ratios from other studies based on an idealized glacier geometry: for example, Reference OerlemansOerlemans (2001) found a ratio of 1.35 for three simple glacier geometries, while Reference Leysinger Vieli and GudmundssonLeysinger Vieli and Gudmundsson (2004) report an average ratio of 1.28 in the case of an advance and 1.46 for a retreat. Only the upper end of our range is higher than the values obtained for idealized glacier geometries, due to the short volume response times we found for the strong negative mass-balance perturbations.
5.2. Climatic perturbation
In the literature the response time of a glacier is usually determined from uniform mass-balance perturbations or equilibrium-line altitude (ELA) changes. In reality, however, a glacier is subject to changes in temperature, precipitation and radiation, and the mass balance does not change equally over the glacier. To investigate the effect on the response time, experiments are launched by varying temperature (between –2.0°C and +3.0°C) and precipitation (from –50% to 50%) separately. For comparison, for each of these simulations an experiment is launched with a spatially uniform mass-balance perturbation over the glacier that corresponds to the average mass-balance perturbation of the particular climatic forcing.
Temperature changes influence the mass balance mostly in the ablation area of the glacier, both for positive and negative perturbations (Fig. 6a and b). This is because temperature is a controlling factor for melting, a process that occurs mainly in the ablation area of the glacier, and because there temperature largely determines the rain or snow fraction. For a temperature decrease the glacier advance is stronger than for a uniform mass-balance forcing over the whole glacier. The final glacier volume is larger, leading to longer length and volume response times (Fig. 7). For a temperature increase the glacier retreats and mainly loses ice at low elevation. The remaining ice at higher elevations is exposed to a less negative mass-balance forcing (compared with the spatially uniform mass-balance forcing) and the total volume loss and glacier retreat is more limited, resulting in shorter length and volume response times.

Fig. 6. Spatial mass-balance forcing for different temperature (a: –2°C, b: +3°C) and precipitation (c: +50%, d: –50%) perturbations.

Fig. 7. Volume and length response times for different climatic perturbations. The corresponding average mass-balance perturbation is given in parentheses. For the two most positive temperature perturbations the length response time could not be determined, as the glacier disintegrates into separate ice patches during its retreat. The simulations start from a steady state with the same length as the present-day glacier, obtained by applying a +0.5mw.e. a–1 mass-balance bias on top of the average 1983–2012 climate. This bias is maintained during the simulations.
For precipitation changes, the dominant mass-balance change occurs at and above the ELA. However, the spatial contrast between the ablation and accumulation area (Fig. 6c and d) is weaker than for the temperature forcing (Fig. 6a and b). For an increase in precipitation the total volume increase and glacier advance are more limited than for a fixed average mass-balance forcing, as for the former the mass-balance increase is confined to the highest areas. This results in slightly shorter response times (Fig. 7). For a precipitation decrease, the area and volume losses are very similar to those for a uniform mass-balance forcing (<1% absolute difference), because the forcing is strongest around the ELA and the spatial contrast in mass-balance forcing is small. The response times are longer than for similar uniform mass-balance forcings as the final volume change is similar, but the forcing is slightly stronger in the upper areas. This is clear for the –10% precipitation forcing (Fig. 7), where the very small mass-balance perturbation initially affects the accumulation area, and the frontal retreat only starts after 32 years.
5.3. Comparison with other response-time definitions
5.3.1. Analytical methods
In the literature, several analytical methods have been presented to determine the response time of a glacier. Some of the older attempts are based on linear kinematic wave theory (Reference NyeNye, 1960, Reference Nye1965) in which the response time is determined as the ratio between the glacier length and the flow velocity at the snout. Applying this to Morteratsch glacier, with a length of 6.3 km and snout velocities <20ma–1, results in a response time above 300 years. This method, in part due to the difficult definition of the snout velocity, usually leads to strong overestimations (Reference Van de Wal and OerlemansVan de Wal and Oerlemans, 1995). Alternatively, this value can be multiplied by the shape factor, the ratio of the average ice thickness change over the glacier to the change at the front (Reference Jóhannesson, Raymond, Waddington and OerlemansJóhannesson and others, 1989; Reference Schwitter and RaymondSchwitter and Raymond, 1993). With a shape factor of ~0.2, the value calculated by Reference Schwitter and RaymondSchwitter and Raymond (1993) for Vadret da Morteratsch, this results in a response time above 60 years, still considerably higher than the values obtained from our numerical experiments.
One of the most used analytical methods defines the volume response time as the ratio between the characteristic ice thickness (H char) and the mass-balance rate at the snout (b snout) (Reference Jóhannesson, Raymond, Waddington and OerlemansJóhannesson and others, 1989):
However, the definition of H char is not straightforward. Often the maximum ice thickness is chosen (e.g. Reference Pelto and HedlundPelto and Hedlund, 2001; Reference Hoelzle, Haeberli, Dischl and PeschkeHoelzle and others, 2003), but this is not per se representative for the whole glacier. This reservation also applies to Morteratsch glacier where the maximum ice thickness of ~360m for the steady-state glacier with present-day length arises from a local bedrock overdeepening. Using the maximum ice thickness as characteristic ice thickness and using a frontal mass-balance rate of –6.3m ice eq. a–1 (value for steady-state glacier with present-day length and corresponding forcing) yields a volume response time of 57 years. As the maximum ice thickness results from an irregularity in the bedrock, it is more appropriate to opt for the average ice thickness along the main flowline (177 m), which is also close to the ice thickness around the equilibrium line. This results in response times between 20.6 and 35.8 years, slightly lower than those obtained from our numerical simulations (Fig. 8, dark blue). An alternative approach is to define the characteristic ice thickness as the change in volume divided by the change in area for a specific glacier change (Reference Harrison, Elsberg, Echelmeyer and KrimmelHarrison and others, 2001). For our numerical steady-state simulations this results in a characteristic ice thickness between 134 (–2.0mw.e. a–1 forcing) and 215m (+1.25mw.e. a–1 forcing). Calculating T e,Jóh with this characteristic ice thickness leads to response times that are in good agreement with the numerical values (Fig. 8, light blue). The Jóhannesson method is known to provide a good estimate for the volume response time of steep glaciers, but underestimates it when the glacier is flatter and the importance of the elevation mass-balance feedback increases (Reference OerlemansOerlemans, 1989, Reference Oerlemans2001; Reference Harrison, Elsberg, Echelmeyer and KrimmelHarrison and others, 2001, Reference Harrison, Raymond, Echelmeyer and Krimmel2003). This is also clear from our simulations, where the main disagreement with the response time from numerical simulations occurs for strong advances, where, due to the flat glacier forefield, the mass-balance elevation feedback becomes important. An approach by which to take the elevation mass-balance feedback into account is proposed by Reference Harrison, Elsberg, Echelmeyer and KrimmelHarrison and others (2001) who introduce the areaaveraged specific balance rate gradient (b grad,av). In their response-time definition:

Fig. 8. Numerical and analytical response times for different mass-balance perturbations. The simulations start from a steady state with the same length as the present-day glacier, obtained by applying a +0.5 m w.e. a–1 mass-balance bias on top of the average 1983–2012 climate. This bias is maintained during the simulations.
where b exp/cov is the average balance rate over the exposed/covered region, close to the balance rate at the snout. The best agreement with the numerical simulations is obtained with the average ice thickness (Fig. 8, orange), while the volume–area thickness scale (proposed in their method) generally leads to overestimations (Fig. 8, red). This result was also found by Reference Leysinger Vieli and GudmundssonLeysinger Vieli and Gudmundsson (2004) who obtained an overestimation with this method by using the volume–area thickness scale, but a good fit when using the average ice thickness. Their finding for an idealized glacier set-up can thus be confirmed here for a real alpine glacier. The overestimation results from the fact that the volume–area thickness scale takes into account the mass-balance feedback implicitly, as it increases together with the feedback. When using the volume–area thickness scale to calculate T e,Har the mass-balance elevation feedback is then taken into account twice.
Reference OerlemansOerlemans (2001) gives an expression for the response time based on the ratio between a length and velocity scale, which for an idealized glacier geometry reads (Reference OerlemansOerlemans, 2012)
Here β is the mass-balance gradient, s is the mean surface slope and L is the equilibrium length; c is a constant obtained from detailed numerical simulations of 15 glaciers and has a value 19.4m3/2 (Reference Leclercq and OerlemansLeclercq and Oerlemans, 2012). For steady-state Morteratsch glacier with present-day length (β = –0.0085 a–1, s = 0.33, L = 6.3 km) this results in a response timescale of 32 years, in the middle of the range obtained by our numerical simulations.
Another analytical method accounting for the glacier geometry is proposed by Reference Raper and BraithwaiteRaper and Braithwaite (2009) using a simple model for glacier hypsometry. They derive an expression for the volume response time equal to T e,Jóh divided by an altitude-range area scaling parameter. This parameter typically varies between 0.3 and 0.4. Applying this scale to Morteratsch glacier results in a volume response time between 55 and 110 years for a retreat, and 80 and 140 years for an advance, considerably higher than those found from our numerical simulations.
5.3.2. Response time of Vadret da Morteratsch reported in the literature
Two other estimates of the response time of Morteratsch glacier have been reported previously (Reference OerlemansOerlemans, 2007, Reference Oerlemans2012). In a first approach Reference OerlemansOerlemans (2007) used the length record of Morteratsch glacier and nearby Palü glacier. The assumption is made that neighbouring glaciers are subject to the same climatic forcing and that the differences in their length record must therefore result from differences in climatic sensitivity and response time. A volume response time of 33 years is obtained for Morteratsch glacier, which is situated in the middle of the range from our numerical simulations. Reference OerlemansOerlemans (2007) found that the climate sensitivity of Morteratsch glacier equals –17.7 m m–1, meaning that the glacier retreats by 1770 m for a 100 m increase in ELA. We obtain a very similar sensitivity from our numerical simulations, in which for the present-day steady-state glacier a –0.5 m w.e. a–1 forcing (71 m ELA rise) leads to 1375 m of retreat, and a forcing of –0.75 m w.e. a–1 (108 m ELA rise) results in 1950 m of retreat. In a more recent publication, Reference OerlemansOerlemans (2012) mentions a response time of 38 years for Vadret da Morteratsch, based on a numerical SIA simulation with a 3-D geometry parameterization (Reference OerlemansOerlemans, 1997). This value is at the higher end of our range and may indicate an overestimation due to the use of the SIA, although this is difficult to verify as the model set-up and parameters are very different.
6. Glacier Response Time in a Changing Climate
So far the response time has been analysed for the present-day glacier size. Here we analyse the effect of the glacier size by forcing glaciers of different sizes obtained from the earlier response-time experiments (Section 5.1) with –0.5 and +0.5 m w.e. a–1 perturbations (Table 1). These are all steady-state glaciers situated in the same topographic setting as the present-day glacier.
Table 1. Volume and length response times for steady-state glaciers of different sizes. The retreat experiment corresponds to an instantaneous mass-balance forcing of –0.5 m w.e. a–1, and the advance experiment corresponds to an instantaneous mass-balance forcing of +0.5 m w.e. a–1

The smallest glacier (7.3 km2) has the shortest response time (Table 1), but for the others there is no clear correlation between the glacier size and response time. For a given perturbation a larger glacier will undergo a larger volume and length change, but the higher flow velocities will compensate for this in terms of response time. A different way to analyse this is from the Jóhannesson or Harrison response time perspective: larger glaciers are thicker (numerator of Eqns (1) and (2)), but reach lower altitudes and thus have a large frontal ablation (denominator of Eqns (1) and (2)). Yet another way to interpret this is from the Oerlemans response-time formulation (Eqn (3)): for an extending glacier (larger L) the surface slope reduces (smaller s) as Morteratsch glacier extends into flatter terrain. τOer response times are close to the response times from the numerical model (Table 1), reproduce the increase in response time with size for the smallest glaciers (7.3– 16.6 km2) and mimic the fact that this is not the case for the largest glaciers (16.6–23.6 km2). The variations in response time between an advance and retreat are mainly related to the bedrock topography and are thus site-specific. A clear example of this is the advancing 11.9 km2 glacier, which has the longest response time. Here the large bedrock depression that corresponds to the present-day high ice thickness area of Vadret da Morteratsch fills up in the vicinity of the front during the glacier’s advance. This process takes a considerable amount of time and causes a large volume change.
In a warming climate Morteratsch glacier will shrink and its response time will thus decrease. This relates to a steepening of the glacier. Furthermore, as temperature rises, more surface melting is expected, which can enhance glacier flow by increased basal sliding and further reduce the glacier’s response time. Some basic sensitivity experiments were performed which indicate a correlation between the response time and the flow parameters (not shown here). This effect is not explicitly taken into account in analytical methods, but may be of importance when comparing different glacier response times on a global scale.
7. Volume–Area Relationship
The steady-state geometries obtained from the previous experiments are used to investigate the relationship between glacier volume and area. This relationship is commonly expressed through volume–area (V–A) scaling, which is the most widely used method to determine the volume of a large sample of glaciers, estimating the volume of individual glaciers as (Reference Macheret, Cherkasov and BobrovaMacheret and others, 1988; Reference Bahr, Meier and PeckhamBahr and others 1997)
where c is the power-law coefficient and γ the exponent. We use 14 different steady states, with different sizes obtained from the mass-balance perturbation experiments (Section 5.1), to test this method (Fig. 9a). Five commonly used sets of parameters from the literature provide a reasonable fit to our glacier geometries (0.76 < R 2 < 0.91, average R 2 = 0.84) (Fig. 9b), but in all cases overestimate the volume of small glaciers and underestimate it for large glaciers. To solve for this, a steeper V–A curve is needed (γ = 2.113 and c = 0.0039 km(3–2γ) provide a best fit, R 2 = 0.993) (Fig. 9b). However, with such a relationship the volume is strongly overestimated for larger glaciers. A possible way to account for this without altering c and γ is by including the average surface slope (S) and a threshold slope (S*) to the V–A scaling:
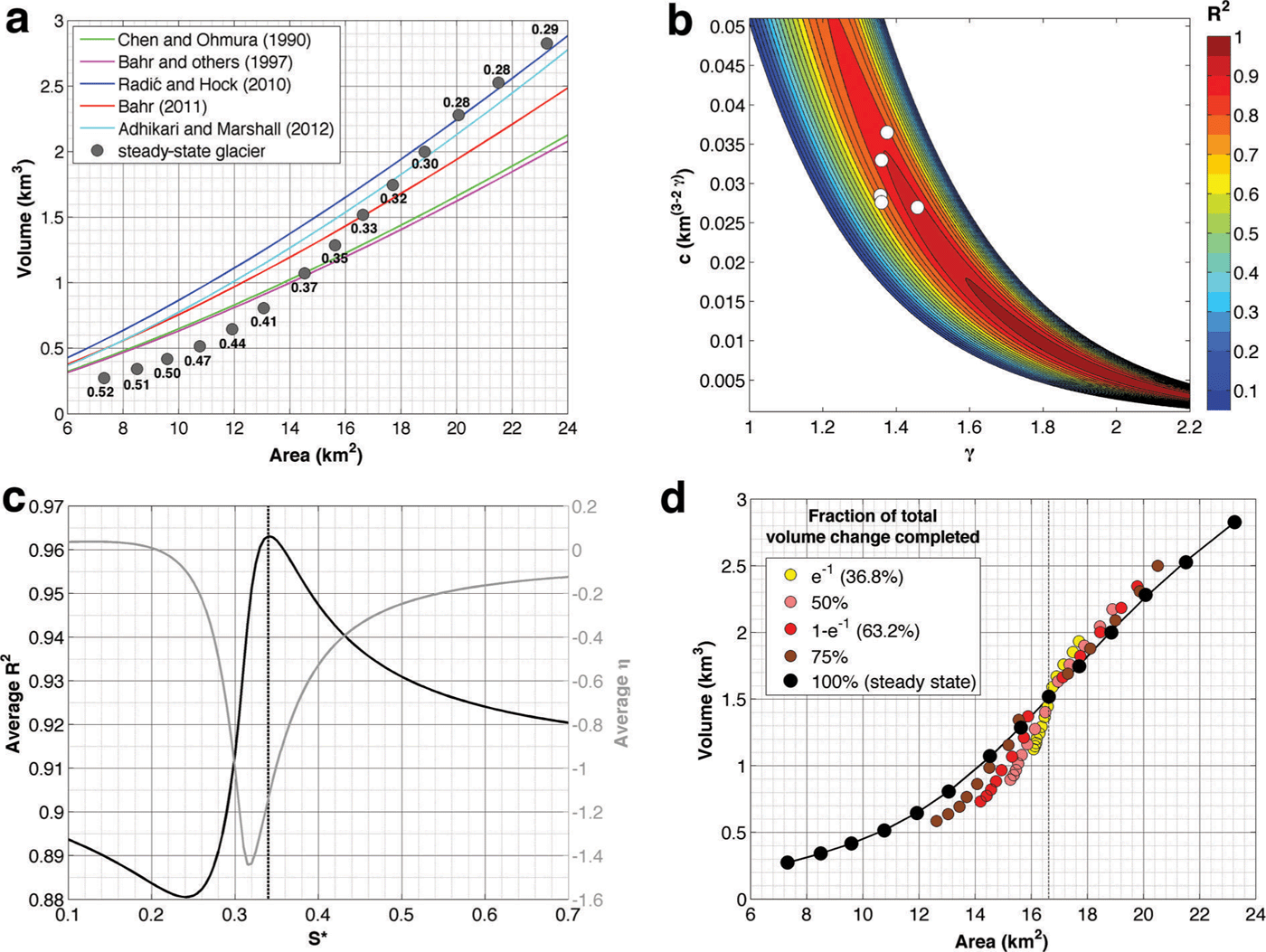
Fig. 9. (a) Glacier volume as a function of glacier area for simulated steady-state glaciers (grey dots; numbers indicate average surface slope) and commonly used V–A relationships: c = 0.0285 km(3–2γ), γ = 1.357 (Reference Chen and OhmuraChen and Ohmura, 1990; R 2 = 0.79); c = 0.0276 km(3–2γ),γ = 1.360 (Reference Bahr, Meier and PeckhamBahr and others (1997), R 2 = 0.76); c = 0.0365 km(3–2γ), γ= 1.375 (Reference Radić and HockRadić and Hock, 2010; R 2 = 0.87); c = 0.033 km(3–2γ), γ = 1.360 (Reference Bahr, Singh, Singh and HaritashyaBahr, 2011; R 2 = 0.89); c = 0.027 km(3–2γ), γ = 1.458 (Reference Adhikari and MarshallAdhikari and Marshall, 2012; R 2 = 0.91). (b) R 2 values between modelled (geometry) and predicted (V–A scaling) volume for different parameter combinations. Parameter space where the R 2 value is <0.05 is left blank. The white dots represent the commonly used V–A relationships (see (a)). (c) Average R 2 between modelled (geometry) and predicted (V–A scaling with slope, Eqn (5)) volume for five parameter combinations (see (a)) as a function of S* and corresponding average η. (d) V–A relationship for steady-state and transient glaciers. The starting point of the transient glaciers is a steady-state glacier with present-day length (dotted black line) and the forcing varies between –2 and +1.25 m w.e. a–1.
Here η is the power-law exponent and S* is the threshold slope above which the scaled volume decreases compared with the classical V–A scaling. For slopes below S* the volume increases. The physical reasoning behind this is that steep slopes (small glaciers in our experiments) translate into a lower ice thickness, while the opposite is true for gentler surface slopes (large glaciers). This inverse relationship between local surface slope and ice thickness follows from plastic flow theory (Reference NyeNye, 1952) and is recurrent in most ice thickness reconstruction methods (e.g. Reference Farinotti, Huss, Bauder, Funk and TrufferFarinotti and others, 2009; Reference Li, Ng, Li, Qin and ChengLi and others, 2012). We evaluate Eqn (5) for five parameter combinations (c and γ) from the literature and find that the average R 2 between the geometries and the scaled volumes is highest for S* = 0.34 (average R 2 = 0.963), for which the average η equals –1.14 (Fig. 9c). With this exponent, halving the surface slope results in a scaled volume multiplication with a factor 2.2 (0.5–1.14), which is close to the inverse relationship (factor 2, 0.5–1) expected between surface slope and ice thickness for plastic flow.
The V–A relationship for transient glacier geometries differs from steady-state geometries as the volume of an ice mass reacts faster to a perturbation than its area (Reference Adhikari and MarshallAdhikari and Marshall, 2012). As a consequence, the volume of a retreating (advancing) glacier is smaller (larger) than for an equal-sized steady-state glacier. The effect of the transient state on the V–A relationship is analysed for the eight retreat experiments (forcing between –0.25 and –2.0 m w.e. a–1) and the five advance experiments (forcing between +0.25 and +1.25 m w.e. a–1) starting from a glacier with the present-day length (Section 5.1) (Fig. 9d). For advancing glaciers the difference between the transient and steady-state volumes, the ‘volume disequilibrium’, is rather limited and is largest (up to 7% on average) early in the evolution, when about a fraction e–1 of the total volume change has occurred. This is in contrast to retreating glaciers where the volume disequilibrium increases with time and is largest (17% on average) around the e-folding volume response time of the glacier. This indicates that the volume disequilibrium is driven mainly by the initial terminus response time of the glacier (shorter for an advancing glacier) rather than by its e-folding response volume time (longer for an advancing glacier).
8. Conclusion
Vadret da Morteratsch has retreated continuously since the end of the LIA, but the imbalance between the glacier geometry and the contemporary climate has never been larger than at present. This implies that, over recent decades, temperatures have risen faster than the geometry was able to adapt to the ongoing warming. The present-day climate– geometry disequilibrium fully determines the glacier’s length evolution in the coming 10–15 years and influences its overall evolution in the coming decades.
Most of our findings are site-specific, but with our calibrated high-resolution model setting provide a good general insight into the response time of a medium-sized alpine glacier. The response time of the glacier was analysed from different perspectives, both for transient and steady-state geometries, and is ~30 years for volume and 50 years for length. We project that these response times will reduce in the future, mainly due to a steepening of the glacier surface, rather than from the reduction in glacier size. Several simple analytical methods provide response times that are in good agreement with those derived from our numerical model, although there is a strong dependence on the chosen characteristic ice thickness scale.
Our experiments stress the importance of the magnitude of the forcing on the response time. However, the effect of the magnitude of the perturbation depends strongly on the glacier’s volume–elevation distribution and bedrock topography. Additionally, a mass-balance forcing associated with a temperature or precipitation change has a spatial pattern, the effects of which hitherto had not been investigated. For a temperature forcing, the length response time typically differs ~5% from a uniform mass-balance forcing of the same average magnitude, while for volume response times this is ~10%. The effect of the forcing’s magnitude through bedrock topography and the volume–elevation distribution as well as the spatial pattern should be studied further in an idealized glacier set-up and accounted for in response-time parameterizations.
V–A scaling was tested for a set of steady-state glaciers and we found that the inclusion of the surface slope and a threshold value were of great benefit to improve the fit. The physical reasoning behind this is that the local surface slope is related to the ice thickness (and thus volume). It will be interesting to test whether this relationship can be tuned and incorporated for a larger sample of glaciers with different topographic and climatic configurations.
Finally, we examined the difference in volume between steady-state geometries and transient glaciers and found that the difference is particularly strong for retreating glaciers. For a medium-sized alpine glacier that was close to steady state in the first half of the 1980s and has since been exposed to a mass-balance forcing between –0.5 and –0.75 m w.e. a–1, we infer that the present-day volume will be of the order of 10–20% smaller than the steady-state volume.
Acknowledgements
We are grateful to MeteoSwiss for providing the meteorological data from Segl Maria and Samedan. The comments and suggestions of two anonymous reviewers and G. Leysinger Vieli helped improve the manuscript greatly. Harry Zekollari holds a PhD fellowship of the Research Foundation – Flanders (FWO-Vlaanderen).











