Introduction
Snowmelt and glacier melt are essential sources of fresh water in western Canada and are strongly affected by climatic conditions (Reference Barnett, Adam and LettenmaierBarnett and others, 2005). Glaciers have the unique ability to store water in years of high snowfall and low temperatures, while supplementing streamflow in years of lower snowfall and higher temperatures (Reference Fountain and TangbornFountain and Tangborn, 1985). Declines in Rocky Mountain snowpack are expected to continue with changing climate (Reference MacDonald, Byrne, Boon and KienzleMacDonald and others, 2012), and mean annual temperatures are expected to increase (Reference Schindler and DonahueSchindler and Donahue, 2006). These factors will further contribute to the glacial retreat that has been observed in the Canadian Rockies since the mid-20th century (e.g. Reference Demuth and BonardiDemuth and others, 2008; Reference Bolch, Menounos and WheateBolch and others, 2010; Reference Tennant, Menounos, Wheate and ClagueTennant and others, 2012). The South Saskatchewan River and its tributaries in southern Alberta, including the Bow River, are believed to be particularly vulnerable to declining mountain runoff (e.g. Reference Rood, Samuelson, Weber and WywrotRood and others, 2005, Reference Rood, Pan, Gill, Franks, Samuelson and Shepherd2008); the river system is fully allocated, mainly for irrigation purposes. The combined effect of these influences will be future increases in water stress in southern Alberta, particularly in light of increasing demand.
Several studies have attempted to quantify glacial contributions to streamflow in the Bow River basin, on the eastern slopes of the Rocky Mountains. Reference Hopkinson and YoungHopkinson and Young (1998) examined statistical relationships between changes in glacier volume and streamflow for the upper Bow River basin. They reported annual glacier contributions to the Bow River at Banff, Alberta, of ~2% on average, between 1952 and 1993. In extremely dry years, they found that glacier volume loss provided up to 50% of late-summer flow in the Bow River at Banff. They also found that significant long-term glacier volume loss reduced the buffering capacity of glaciers in times of low flow.
Reference Demuth and BonardiDemuth and others (2008) focused on mass-balance and volume reconstructions of benchmark glaciers in the southern and northern Cordillera, specifically Peyto Glacier located just north of the Bow River basin. They found that small glaciers showed a marked decrease in volume over the 20th century, as well as negative mass-balance trends since 1880. According to the study, this has led to decreased flows in the Nelson River system, of which the Bow is a sub-basin. The hydrological model WATFLOOD was used by Reference Comeau, Pietroniro and DemuthComeau and others (2009) to estimate glacial and snowmelt contributions to the Bow River from 1975 to 1998. They concluded that shifts in flow timing will be the main impact of future glacier recession on streamflow and expect this to manifest as earlier peak flows and lower flows in late summer. Reference MarshallMarshall and others (2011) used a combination of simplistic models of glacier mass balance and glacier dynamics to estimate glacial contributions to streamflow along the eastern Rocky Mountain front. Reference MarshallMarshall and others (2011) provided the only estimate of future glacial contributions to the Bow River.
The language used to describe glacier melt varies greatly between studies. For the purpose of this study, we refer to snowmelt, ice melt and volume loss. During the course of any melt season, exposed glacier ice melts; in this study, snowmelt refers to melting of seasonal snow (i.e. the winter snowpack) and ice melt includes any melting of exposed ice or firn (i.e. multi-year snow and ice that has been stored on the glacier). Volume loss refers to the ice melt which is a result of negative mass balance. In years of negative mass balance, ice melt will generally be higher than volume loss, because some snow in the accumulation area of the glacier goes into storage. In years of positive mass balance, there is no volume loss, but ice melt will still occur. Snowmelt in our study includes melt of all snow from glacier surfaces, but not the surrounding terrain.
The future of water management in southern Alberta will depend on reliable knowledge of glacial meltwater resources in the region. While the current body of knowledge provides some insight, there is a need for better understanding in order to inform water management. This study develops a new distributed melt model to estimate glacial contributions to the Bow River in the early 21st century.
Study Area
Bow River basin
The Bow River basin, located in southern Alberta, is a sub-basin of the South Saskatchewan River, part of the larger Nelson drainage system. The headwaters are on the continental divide in the Eastern Front Range of the Canadian Rocky Mountains and the river runs east roughly 400 km before joining the North Saskatchewan River (Fig. 1). There are several population centres in the basin, including the city of Calgary and the towns of Banff, Canmore and Cochrane. In addition to municipal water uses, there are high agricultural water demands. Of the annual flow in the South Saskatchewan, 60-70% is allocated through provincial permits, and the basin is now closed to further allocations (http://environment.alberta.ca/01722.html). A number of glaciers supplement water flow in the Bow River, most notably Bow and Crowfoot Glaciers, which are outlets of the Wapta Icefield.
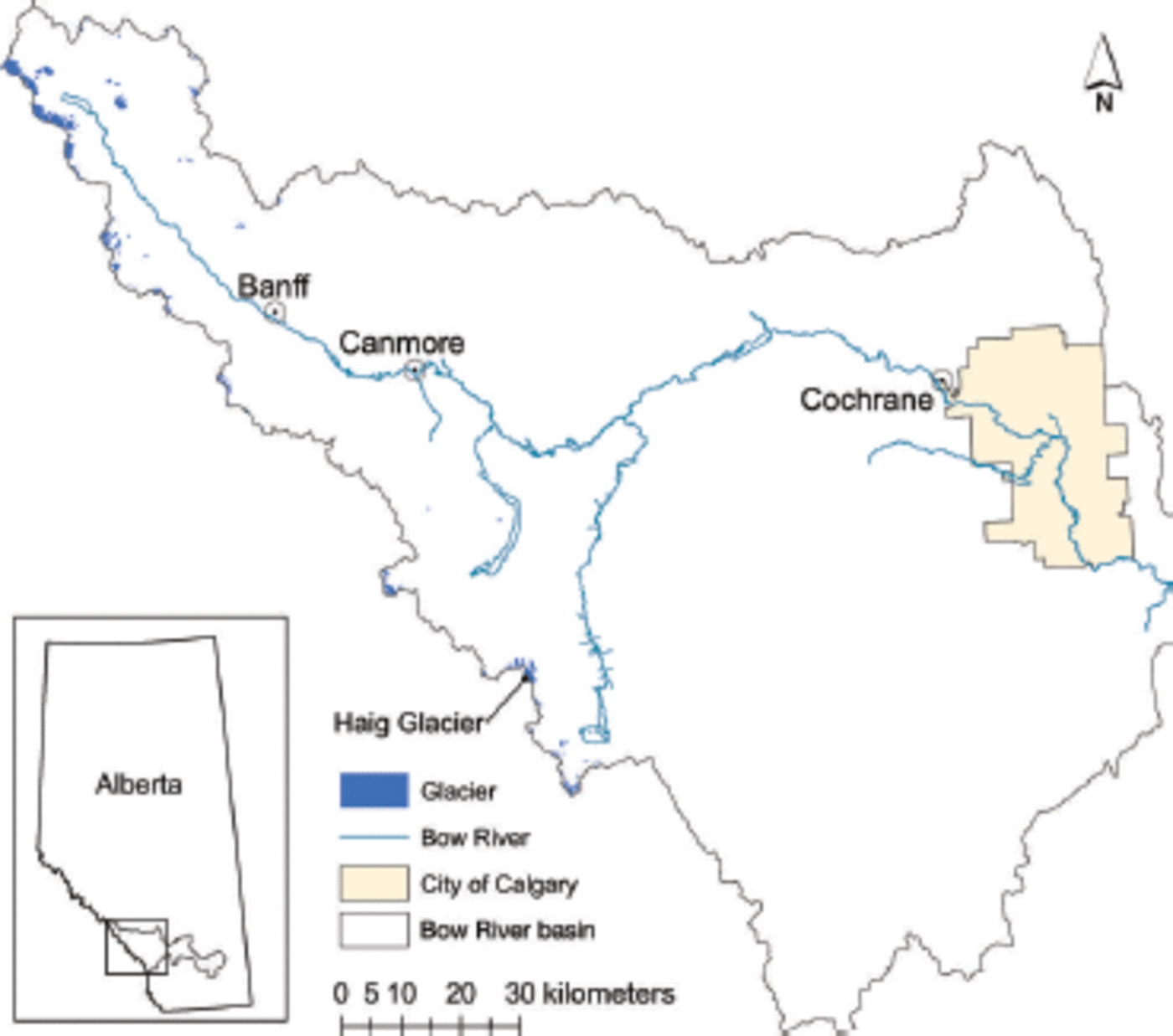
Fig. 1. The Bow River basin, southern Alberta, has headwaters on the continental divide in the Eastern Front Range of the Canadian Rocky Mountains. Haig Glacier, indicated in the southern portion of the basin, has been the focus of ongoing glaciological study, including mass-balance and meteorological measurements.
The largest contiguous ice mass in the basin is 11 km2, and includes the two above-mentioned glaciers, as well as a portion of the icefield. For the purpose of this study, only ice bodies >0.1 km2 were included. With this stipulation, 73 ice bodies were identified in the basin, covering 57 km2. The average area of these glaciers is 0.8 km2. The glaciers of the basin span an elevation range of 1900-3500 m, with 74% of glacier area existing between 2500 and 2900 m.
Peyto Glacier, another outlet of the Wapta Icefield feeding the North Saskatchewan River basin, has been monitored by different agencies of the Government of Canada since 1966. Though it does not feed into the Bow River, it is within a few kilometers of the Bow River headwaters, and the extensive data record at Peyto Glacier is useful for comparison purposes in this study. Peyto Glacier is 12 km2 and has an elevation range of 2100-3150 m (Reference Hopkinson, Chasmer, Munro and DemuthHopkinson and others, 2010). This spans the elevation range of most glacier coverage in the basin.
Basin-wide analysis is based on a digital elevation model (DEM) developed by Christina Tennant at the University of Northern British Columbia (UNBC). The DEM is based on Shuttle Radar Topography Mission 3, which was resampled to 100m resolution. Glacier inventory data, based on Landsat imagery from 2004-06, are used to delineate glacier coverage in the basin. The inventory was generated and manually checked in 2008 (Reference Bolch, Menounos and WheateBolch and others, 2010). It includes ice bodies of at least 0.05 km2.
Daily meteorological data for Banff, as well as monthly temperature data from Banff and other stations, were downloaded from Environment Canada (http://www. climate.weatheroffice.gc.ca/climateData/canada_e.html). Archived snow pillow and snow depth data are collected by Alberta Environment. Mass-balance data from Peyto Glacier were obtained through the World Glacier Monitoring Service. Winter, summer and annual balance are reported at Peyto Glacier until 1995, after which only net-annual balance is reported.
Regional cloud cover is available at a resolution of 210 km as part of the US National Centers for Environmental Prediction (NCEP) Reanalysis data, provided by the US National Oceanic and Atmospheric Administration Physical Sciences Division (Reference KalnayKalnay and others, 1996).
Hydrometric data were obtained for the Bow River at Banff and Calgary. Historical daily discharge at Banff from 1912 to 2009 was downloaded from the Water Survey of Canada (http://www.wsc.ec.gc.ca/hydat/H2O/index_e.cfm). Mean weekly discharges and naturalized discharges at Calgary were obtained from Alberta Environment (Water Sciences Branch, unpublished).
Haig Glacier
Haig Glacier lies in the southern portion of the Bow River basin on the eastern slopes of the Canadian Rocky Mountains, -100 km southwest of Calgary. Sloping gently southeast from the British Columbia-Alberta border, it spans an elevation range of 485 m, from 2435 to 2920 m at the continental divide, and has a total area of -2.8 km2. Haig Glacier is the largest outlet of a small icefield, which also includes French Glacier to the north and an unnamed glacier to the west. Though it is slightly larger than the average glacier in the basin, Haig Glacier, like Peyto Glacier, spans the elevation range of most glacier coverage in the basin. The median elevation of Haig Glacier is 2662 m, compared with 2620 m for the median elevation of all glaciers in the Bow River basin (Reference MarshallMarshall and others, 2011). Combined with the availability of data, this glacier provides a good setting for development of modelling techniques for use over the entire basin.
Haig Glacier has been a site of ongoing glaciological study since 2001, including mass-balance surveys, runoff monitoring and measurement of meteorological variables. An automatic weather station (AWS) is situated at 2600 m, roughly coinciding with the equilibrium line, while a second is situated in the glacier forefield at 2335 m. Each AWS consists of a Campbell Scientific CR1000 data logger, solar panel, anemometer, four-component radiometer, temperature and humidity sensor in a radiation shield, and ultrasonic distance sensor. In addition, the forefield AWS has both a pressure sensor and a rain gauge. The forefield station is set up on an aluminum tripod, while the glacier station is mounted on a mast drilled into the ice. The glacier station has migrated over time with the movement of the glacier and periodically must be redrilled due to melting out, which at times leads to leaning of the mast. As a result of this, the glacier station has a number of data gaps. Both stations collect data at 10s intervals and record 30 min averages.
Winter balance surveys were conducted each year (2002–10) between late April and early June, consisting of centreline depth measurements and two to four snowpack density profiles. Significant wind redistribution was observed during the surveys. Melt measurements were collected along the centre line periodically throughout most summers to give an ongoing picture of melt over the course of a given season. The snow accumulation and mass-balance regime for Haig Glacier are discussed in Reference Adhikari and MarshallAdhikari and Marshall (2013).
Melt Model
In this section we describe the theoretical basis of the melt model, the data sources used to constrain and evaluate the model, and the methods deployed to extend the model to the Bow River basin. There are three stages to the model development: (1) model calibration at the Haig Glacier AWS site; (2) extension to a distributed snow accumulation and melt model for Haig Glacier, based on far-field meteorological data and cloud cover from a climate model; and (3) extension of this simplified distributed model, which has no in situ meteorological or glaciological data requirements, to the Bow basin. The methods section explains each stage of model development, and model calibration (optimized parameters) and performance assessment are discussed in the results.
Theory
Given the basin-wide scope of this study, we focus on developing a physically based melt model that does not rely heavily on measured data. While a full energy-balance model would be ideal for understanding melt processes, the heavy data requirements make it a poor choice for large-scale modelling, such as that undertaken in this study. Degree-day models, in contrast, provide a model with few data requirements, but lose some of the detail of energy-balance models, particularly in complex terrain where solar radiation inputs are highly variable.
Temperature-index models incorporating solar radiation have been shown to perform equally with full energy-balance methods in regional-scale studies (Reference HockHock, 2005). In addition, temperature-index methods are simpler to apply to catchment- or regional-scale melt modelling, where high-resolution meteorological inputs needed for more complete energy-balance models are difficult to obtain. The enhanced temperature-index model (Reference HockHock, 1999), which includes potential direct clear-sky radiation, is probably the most widely used for distributed melt modelling (e.g. Reference Verbunt, Gurtz, Jasper, Lang, Warmerdam and ZappaVerbunt and others, 2003; Reference Zappa, Pos, Strasser, Warmerdam and GurtzZappa and others, 2003; Reference Huss, Farinotti, Bauder and FunkHuss and others, 2008). Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005) discussed shortfalls of this model, most importantly the incorporation of a simplistic reflectance term, rather than true surface albedo. Snow and ice albedo vary dramatically throughout the melt season, and changes in albedo can account for a significant proportion of melt by increasing or decreasing absorbed radiation. In addition, the radiation factor is based on potential direct rather than actual solar radiation, so the model is not sensitive to varying cloud conditions at different sites or through the melt season. The Reference HockHock (1999) model is essentially a degree-day model, with the melt factor varying in space based on potential radiation. Alternatively, treating radiation and temperature separately allows the influence of each to be treated independently (Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others, 2005).
Both Reference AnslowAnslow (2004) and Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005) present a modification of the temperature-index model by including measured albedo and incoming (surface-level) solar radiation in a melt model. This modification makes for a more complex model, but begins to bridge the gap between energy-balance and degree-day models. With separated absorbed radiation and temperature, the model comes closer to treating melt as a physical, rather than an empirical, process. A linear combination of these two variables, however, must necessarily include overlapping influence from the effect of radiation on temperature. This relationship can be ignored in Reference HockHock (1999), because the albedo and radiation terms are included in the coefficient, rather than as independent variables. Anslow suggested removing the variance of temperature due to radiation by regressing radiation on temperature. The residual of this regression is the input to a new melt model. This method was applied by Reference Shea, Anslow and MarshallShea and others (2005), but not fully explored. Building on the work of Reference AnslowAnslow (2004), Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005) and Reference Shea, Anslow and MarshallShea and others (2005), this study explores a model using temperature and absorbed solar radiation which addresses the problem of collinearity pointed out by Reference AnslowAnslow (2004).
Model formulation at Haig Glacier AWS
Four datasets from the summers of 2002–04 at the Haig Glacier AWS are used to parameterize the relationship between melt, temperature and solar radiation to model summer melt at the location of the AWS. These are melt (from an ultrasonic distance sensor), air temperature, incoming and outgoing shortwave radiation. The melt model development is restricted to the May–August period, the main melt season at this site.
For model development and comparison, melt is determined by the change in snow depth or ice surface position measured by an ultrasonic distance sensor at the AWS. To calculate melt (M), the average depth at the beginning of a melt period is subtracted from the average depth at the end of the period. The change in depth (cm) is converted to mm w.e. using the density of snow or ice. The densities of both glacier ice and new snow are based on the median of a range of values in Reference PatersonPaterson (1994), with new snow set to 150kgm–3 and ice to 874 kgm– 3 . The density of old snow is determined by relating the Julian day to densities measured at Haig Glacier (i.e. snow age through the melt season, which crudely accounts for snow densification and snowwater content). Melt-season values range from 300 to 450 kgm– 3.
Depth records are inherently noisy, and daily surface height changes are of the order of a few cm, giving a low signal-to-noise ratio, so depth changes were based on 5 day periods of melt, as opposed to daily or hourly changes. For this reason, all other model variables described below were aggregated to 5 day periods.
New snow events are identified as positive changes in depth during the summer months using a time-series plot of depth. These are isolated manually and snow accumulation is calculated as the depth at the end of snowfall minus the depth at the beginning of snowfall.
The amount of radiation absorbed at the glacier surface (i.e. the energy available for melt) is calculated by subtracting measured outgoing radiation from measured incoming radiation. For aggregation into 5 day periods, daily absorbed radiation (I abs; MJm–2d–1) is first calculated based on daily total incoming and outgoing radiation. The total absorbed radiation for each day is then summed into 5 day periods.
Energy from absorbed shortwave radiation affects air temperature in the glacier boundary layer, leading to close linkages between these two measurements. Using daytime temperature (08:00-20:00) and absorbed radiation data from all three summer seasons, a relationship between the variables is modelled through linear regression, TI = η + βIabs. The residual temperature, T res, is determined by subtracting TI from the near-surface air temperature, T, for daytime hours. T res is interpreted as the air temperature due to heating other than solar radiation, such as longwave radiation and sensible heat flux.
Half-hourly recorded temperature and daily absorbed radiation values are used to calculate T res, which is then summed into 5 day positive degree-day totals (PDDres). By using PDD in the model, temperatures below 0°C have no negative effect on melt (i.e. negative temperatures do not decrease the amount of melt). The measured temperature is also summed into 5 day PDD to assess whether temperatures were >0°C, enabling melt.
The variables described above are combined to form the final melt model, where MF and RF are free parameters:
In this form, times of melt and no melt are separated using real air temperature. The residual temperature contributes to melt at times when it is above zero, but all melt is attributed to solar radiation when the residual temperature is negative (PDDres = 0).
The performance of the model is evaluated through a comparison of measured and predicted melt for the 2007 summer season. Haig Glacier data from 2002 to 2004 are also used to calibrate the model developed by Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005) and the results of both models are compared for summer 2007 using the Nash-Sutcliffe coefficient:
where M is 5 day measured melt, M is modeled melt and M is the average 5 day measured melt for the season. The subscript i refers to the ith 5 day time-step in the model.
Distributed model formulation
The calibrated model described above is applied over the surface of Haig Glacier using modelled inputs. The different models used to estimate the inputs for Eqn (1) are described below. Although we have detailed data from Haig Glacier, we develop a basin-wide model for snow accumulation, temperature, cloud cover and solar radiation, based on meteorological observations at a distant ‘index site’ (Banff) and US National Centers for Environmental Prediction (NCEP) Reanalysis. Modelled fields can then be compared with detailed measurements at Haig Glacier to assess the performance of the regional model. This is of course inferior to the actual data for modelling of Haig Glacier mass balance, but it is a more suitable approach for regional-scale and future modelling.
Several functions to predict initial snow depth on the glacier surface are explored for use in this study, including traditional linear precipitation lapse rates, exponential lapse rates and multivariate models based on regional snow data accumulation at Haig and Peyto Glaciers. We parameterize glacier snowpack based on valley-bottom precipitation measurements at a central location in the Bow basin, Banff, which has an elevation of 1397 m. The final model choice is described in detail below.
Summer snowfall also plays an important role in the model, particularly for estimating albedo. A study of summer precipitation lapse rates in the Eastern Canadian Rockies yielded no statistically significant results (Reference Shea, Marshall and LivingstonShea and others, 2004), which suggests that orographic controls on summer precipitation are weak in this region. Summer snowfall data available for this study are limited to Haig Glacier, which is likely not representative of snowfall over the entire basin. As an alternative, summer precipitation over the basin is modelled as equal to precipitation recorded at Banff. Snowfall is assumed to occur when elevation-lapsed temperatures are <0°C. The performance of this assumption is examined at the Haig Glacier AWS for 2002–03 using a confusion matrix and by calculating the percentage difference in total snowfall for both summers.
Radiation absorbed at the glacier surface is estimated based on three separate models. First, daily potential radiation is calculated for each point on the glacier surface, then modified by a cloud cover factor to estimate incoming solar radiation. The absorbed radiation is then estimated through a modelled surface albedo. This modelled absorbed radiation at each point on the glacier is input into the melt model described in Eqn (1).
A well-established method for calculating potential direct solar radiation, IP , is laid out in Reference OkeOke (1987). It relies on geographic information available through the DEM, the date and the time of the calculation. The equations are
In Eqn (3), I
0 is the solar constant (1368 Wm–2), ![]() is the eccentricity correction factor of the Earth’s orbit, with R the instantaneous Earth-Sun distance and Rm the mean Earth-Sun distance, 𝜓 = 0.75 is the constant clear-sky transmissivity, optimized for Haig Glacier by Reference SchafferSchaffer (2010), P is atmospheric pressure and P
0 is mean atmospheric pressure at sea level. The local zenith angle, Z, is calculated as a function of latitude, hour angle and solar declination. The hour angle is a function of the time of day (i.e. 1-24), and the solar declination is a function of the time of year.
is the eccentricity correction factor of the Earth’s orbit, with R the instantaneous Earth-Sun distance and Rm the mean Earth-Sun distance, 𝜓 = 0.75 is the constant clear-sky transmissivity, optimized for Haig Glacier by Reference SchafferSchaffer (2010), P is atmospheric pressure and P
0 is mean atmospheric pressure at sea level. The local zenith angle, Z, is calculated as a function of latitude, hour angle and solar declination. The hour angle is a function of the time of day (i.e. 1-24), and the solar declination is a function of the time of year.
In Eqn (4), the effects of radiation incident on an angled surface are accounted for, with ![]() being the surface slope angle, 𝜙sun the solar azimuth angle and 𝜙slope the slope azimuth angle. Solar azimuth angle is a function of longitude, hour angle and solar declination.
being the surface slope angle, 𝜙sun the solar azimuth angle and 𝜙slope the slope azimuth angle. Solar azimuth angle is a function of longitude, hour angle and solar declination.
For regional modelling, cloud cover over the study area is taken directly from NCEP Reanalysis data. NCEP Reanalysis provides cloud cover as a fraction over the entire atmospheric column, fc, and potential incoming radiation is multiplied by (1 - fc) to reduce radiation incident on the ground. Daily incoming radiation is then summed into 5 day periods for use in the model. Incoming radiation calculated using NCEP cloud cover is compared with radiation calculated using cloud cover estimated from local data at Haig Glacier, using a ratio of measured incoming radiation to potential radiation in the glacier forefield. Data collection at this site is unaffected by station movement, and the radiometer maintains a truer horizontal position.
Glacier surface albedo is affected by a number of factors, including snow depth, grain size, presence of impurities, and water content (Reference HockHock, 2005). Reference Brock, Willis and SharpBrock and others (2000) undertook an extensive study of albedo modelling. Based on an analysis of different model parameters, the study outlines a model of glacier surface albedo which relies on snow depth and timing of snow events. For deep snow (>11 cm w.e.) the surface albedo is unaffected by underlying ice. Instead, albedo is controlled by snow age, which is a proxy for grain size and concentration of impurities. Reference Brock, Willis and SharpBrock and others (2000) found that for deep snow, albedo decreases logarithmically with increasing accumulated PDD since snowfall. This relationship changes to an exponential decay when shallow snow depths are reached (<11 cm w.e.). In both cases the albedo is ‘reset’ to a new snow albedo when snowfall events occur, by resetting the cumulative PDD. We follow this approach, with coefficients in the albedo model based on the work of Reference SchafferSchaffer (2010) on Haig Glacier. The albedo is calculated as a 5 day average based on 5 day melt from the previous period, daily snow accumulation and daily accumulated positive temperature. Daily snow accumulation is used to reset accumulated PDD, in order to capture mid-period changes in albedo. We specify a fixed albedo of 0.23, based on late-summer (bare ice) albedo at the Haig Glacier AWS during the summers of 2002-04.
Temperature for degree-day melt models is most commonly estimated using a reference station (Banff, in our case) along with linear lapse rates to adjust for cooling with elevation. A number of studies report average environmental lapse rates in mountainous regions (e.g. Reference Martinec and RangoMartinec and Rango, 1986; Reference RollandRolland, 2003; Reference Lundquist and CayanLundquist and Cayan, 2007).
For this study, monthly summer lapse rates are calculated using average temperature from seven weather stations, including two AWS sites at Haig Glacier and five Environment Canada monitoring stations. Lapse rates are determined for May, June, July and August, from 2002 to 2004. The final lapse rates are taken as an average of each month over the three years.
Glaciers have cooling effects on temperatures. Glacier ice and snow temperatures are held at 0°C while melting occurs, which in turn lowers near-surface air temperatures. Reference Flowers, Marshall, Björnsson and ClarkeFlowers and others (2005) use this knowledge to determine a constant ΔT, to represent the near-surface air temperature cooling effect. A similar approach is undertaken in this study. A correction factor is calculated, in conjunction with the lapse rates described above, by optimizing the Nash-Sutcliffe statistic comparing modelled and measured temperatures on Haig Glacier. Daily average and maximum temperatures, ![]() and
and ![]() , are modelled using the modified lapse rate described above.
, are modelled using the modified lapse rate described above.
PDD are calculated most accurately using hourly or sub-hourly timescales. Without this resolution, days with average temperatures below 0°C will have no modelled PDD, whereas in reality some period of the day may have positive temperatures. Reference ReehReeh (1991) used a sine function to model annual temperature distribution for the purpose of degree-day modelling. In this method, the sine curve describing temperature distribution is centred around the average temperature, with an amplitude equal to the range between the maximum and average. Reference SchafferSchaffer (2010) models daily temperature distribution at Haig Glacier using the same method. Reference SchafferSchaffer (2010) introduces a lag of 6 hours in order to match data obtained at Haig Glacier for the daily temperature cycle (Eqn (5)). This shift was also used in this study.
where t refers to the hour of the day and t T = 24 is the total hours in the day.
To calculate PDDres, temperatures calculated in Eqn (5) between 08:00 and 20:00 are modified to remove the influence of absorbed radiation. Temperatures between 08:00 and 20:00 are left as calculated. Once a new daily distribution is determined, positive temperature hours are summed into modelled residual PDD and used as input for the melt model.
Modelled variables isolated at the Haig Glacier AWS location are compared to measured variables during summer 2007.
Results
Calibration and model performance
The correlation between average daytime temperature and absorbed solar radiation at the AWS for the summers of 2002-04 is 0.70. Linear regression is used to find the coefficients η and β for computing T res. Equation (6) is the tuned model used to compute the influence of radiation on temperature.
After removing the influence of absorbed radiation, the correlation between T res and I abs is reduced to almost zero, showing that residual temperature is not correlated with absorbed radiation.
Using ordinary least-squares regression and employing the residual temperatures calculated from Eqn (6), Eqn (1) is calibrated with 2002–04 summer data from the glacier AWS. The calibrated model is given by
where M refers to total 5 day melt (mm w.e.) based on cumulative absorbed radiation and PDDres over 5 day periods. While the constant intercept in this equation theoretically permits ‘negative’ melt, this situation does not arise because 5 day absorbed radiation and PDDres totals are always well above zero at times when PDD>0°Cd.
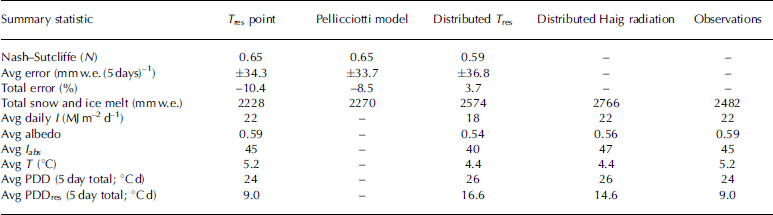
The model is tested by calculating melt using an independent dataset from summer 2007 (Fig. 2). The model overestimates melt for some 5 day periods, particularly in late summer, while underestimating in other 5 day periods (e.g. in May). The average absolute error is 34.3 mmw.e. for a 5 day period, which corresponds to an average deviation of 30%. Overall the model under-predicts melt by 10% for summer 2007. The Nash–Sutcliffe coefficient is found to be 0.65 (Table 1). This value indicates the model accounts for a larger portion of the variability in measured melt than the average melt value for the season. By contrast, a negative N value would indicate that average melt would be a better predictor of melt than the model, for a given 5 day period.
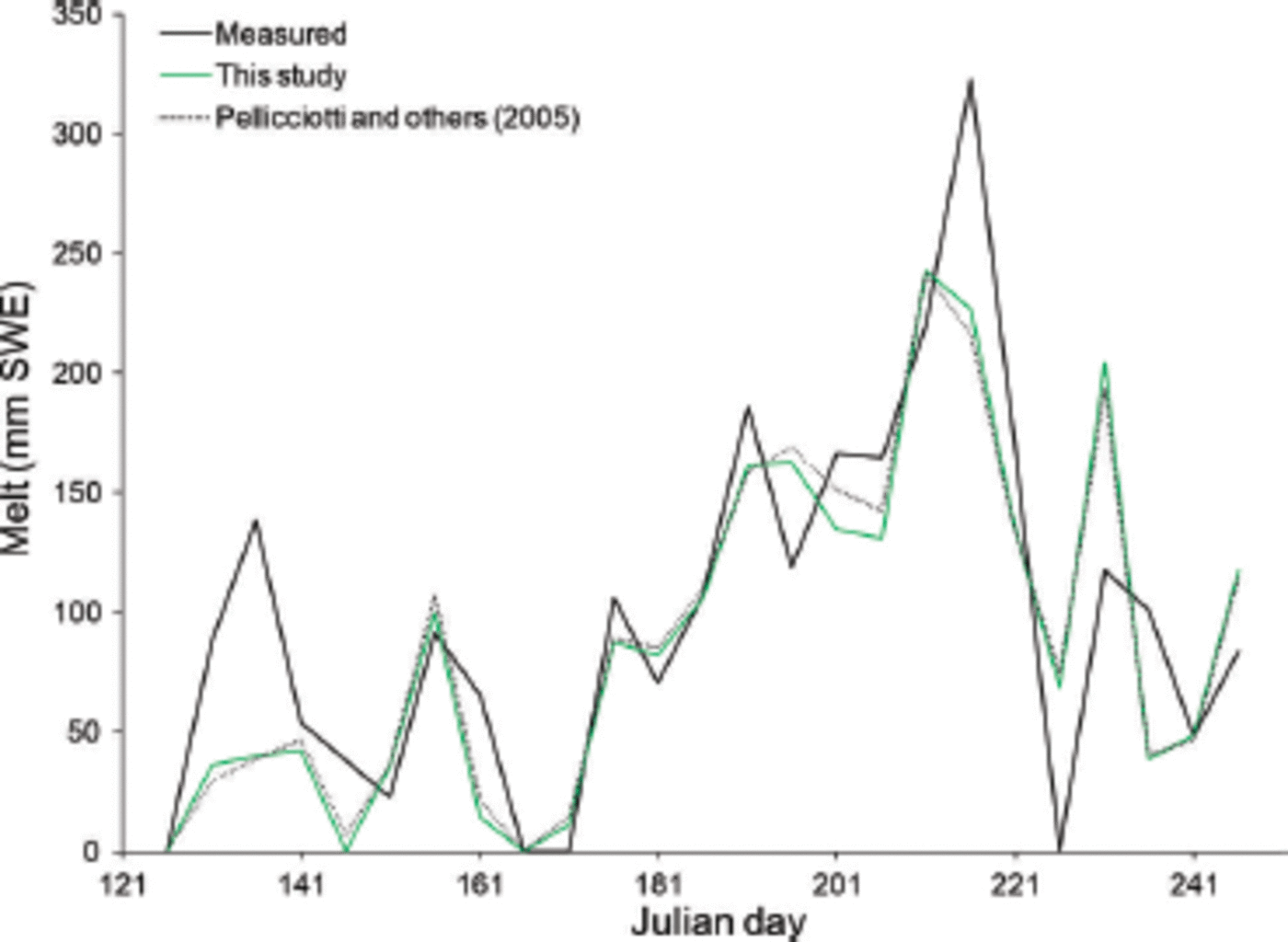
Fig. 2. Predicted and measured 5day melt totals at Haig Glacier during the 2007 melt season.
Table 1. Performance of three melt models at the Haig Glacier AWS using summer 2007 data
With the correlation between absorbed radiation and temperature removed, the influence of each variable on melt can be examined. On average, 80% of summer melt is attributable to absorbed radiation. The remaining 20% comes from residual temperature, the proxy for other terms in the energy-balance equation. The influence of temperature peaks in July when residual PDD is highest and absorbed radiation has not yet reached its maximum. In May, temperatures are often below freezing, and melt is almost entirely due to absorbed radiation.
For comparison purposes the 2002-04 data from Haig Glacier are also used to calibrate the model described by Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005). Summer 2007 data are then used to test the model against measured melt as well as melt modelled using Eqn (7). The results of the model run are summarized in Table 1. The two melt models perform equally well, with the same Nash-Sutcliffe coefficient and similar errors.
Distributed model evaluation
The distributed model is initialized using modelled snow-pack and applied over Haig Glacier for the 2007 melt season using modelled inputs. Modelled variables isolated for the location of the Haig Glacier AWS are evaluated through comparison with measured data (Fig. 3 and 4). Statistical results are summarized in Table 1. The Nash-Sutcliffe statistic is slightly lower (N = 0:59) than that of the point models described above, indicating the model still performs better than assigning an average melt value for each period. The model overestimates melt by 4% and has an average absolute error of 36.8 mm w.e. (5 days)–1 (Fig. 3d).

Fig. 3. Measured vs modelled input fields for the radiation–temperature melt model for 5 day periods from 1 May to 30 September 2007. (a) Positive degree-days (PDD); (b) residual PDD; (c) incoming (asterisks) and absorbed (diamonds) solar radiation totals; and (d) snow/ice melt. Each plot shows 1 : 1 lines.

Fig. 4. Measured (black) and modelled (green) input fields for the radiation–temperature melt model, 1 May to 30 September 2007. (a) 5 day PDD totals; (b) residual 5 day PDD totals; (c) 5 day incoming solar radiation totals; and (d) albedo. The orange line in (d) shows the daily albedo data, and the black line is the 5 day average. Diamonds indicate the modelled fresh-snow events (right axis).
Initial snowpack
As described above, several models were explored for estimating 1 May snowpack at both Haig and Peyto Glaciers. A linear lapse rate model captures average snowfall at both glaciers, lacks the steep gradient observed in snow depth over glacier surfaces and the inaccurate distribution of snow poses problems for model performance. While an exponential lapse rate is able to produce a steeper gradient of snow accumulation, predicted snowfall at high elevations is greatly overestimated. Instead, a multivariate model using winter (October-April) precipitation in Banff (P B, mm) and elevation, z (m), is fit to 1 May snow distribution along the centre line of Peyto Glacier. The optimized fit to winter balance data at Peyto Glacier, bw(z), has an R2 = 0.82 and the final model is given by
The model is applied at Haig Glacier for the summers of 2004 and 2005. The comparison reveals lower correlation along the centre line than Peyto Glacier, R2 = 0:35 in 2004 and R2 = 0:20 in 2005 (Fig. 5). Wind redistribution at Haig Glacier creates a highly irregular distribution pattern which is unlikely to reflect snow cover elsewhere in the basin (Fig. 5). This approach is obviously too simple, but few data on high-elevation snowpack are available to refine this further, given the local nature of wind redistribution. The model is used to compute winter balance at both glaciers for comparison to measured winter balance. Winter mass-balance data are available from Haig Glacier from 2002-05 and 2009-13. For these years, modelled winter mass balance has a bias of-290 mm w.e. Winter balance at Peyto Glacier was computed for 1985-95, and the mean bias for this period is -50 mm w.e. Because the majority of glaciers in the Bow River basin are in closer proximity to Peyto Glacier than to Haig Glacier and the elevation range of Peyto Glacier is more representative of the basin hypsometry, Eqn (8) is used to simulate winter snowpack on all the glaciers of the basin.
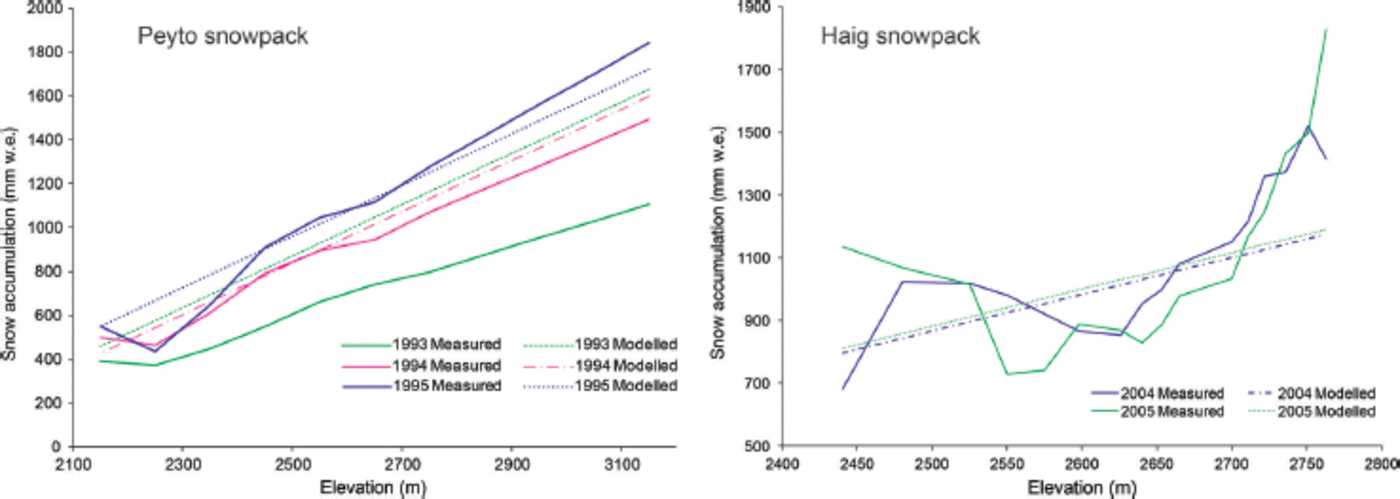
Fig. 5. Measured and modelled winter snowpack using a linear function at Peyto and Haig Glaciers.
Incoming solar radiation
Figure 4c shows 5 day totals of measured and modelled incoming solar radiation at Haig Glacier during 2007 for the distributed model. The correlation between measured and modelled daily incoming radiation is 0.23. The general patterns of daily and seasonal variability are still present, but the modelled daily average incoming radiation is ~18% less than observed (22 and 18MJm–2d–1 , respectively). NCEP cloud cover leads to too much attenuation of incoming radiation in summer 2007. A separate simulation, using cloud cover estimations from Haig Glacier in place of NCEP cloud cover, has a correlation between measured and modelled radiation of 0.91, a large improvement that is expected using locally derived cloud cover estimates. The average daily value is 22 MJm-2d–1, in accordance with observations, and total melt at the AWS is 2766 mmw.e., 200 mm greater than the simulation using NCEP cloud cover.
Albedo
The modelled albedo shows the overall trend of measured albedo (Fig. 4d). The model is also able to capture the response to summer snowfall events, seen through the correspondence of spikes in albedo to new snow. Early- and midsummer albedo are generally underestimated, while late-summer ice albedo is higher than measured. The overall average albedo is lower than measured, 0.54 and 0.59 respectively.
Summer snow events
Summer snow events, which feed into the albedo model, are assessed using a confusion matrix comparing the timing of modelled snow events to that of measured events during the summers of 2002 and 2003, independent of magnitude. The model predicts timed snow events correctly 61% of the time. Coincidentally, the number of total modelled snow events is equal to the number of measured snow events. The total modelled summer snowfall for the two summers is 124 mm w.e., which represents only 25% of the total measured summer snowfall for these summers. Total snowfall in the 2007 model run is closer to measured, 105 mm w.e. compared to 122 mmw.e.
Absorbed radiation
Modelled albedo and incoming radiation both feed into the calculation of absorbed incoming radiation, which is an essential input to the melt model and the calculation of T res. The model tends to underestimate absorbed radiation throughout the summer (Fig. 3c); overall I abs is underestimated by 8.7%. This is a result of the underestimation of incoming radiation (Fig. 4c), but the impact is partially compensated by the lower average albedo in the model. The average 5day absorbed radiation from the model is 40 MJ m–2, compared with 45 MJ m–2 for measured absorbed radiation.
Near-surface air temperature
Monthly air temperature lapse rates developed for this study range from -0.0060 to -0.0055°Cm–1. Using these lapse rates, the temperature shift, AΔT, is calculated for the period 2002-04. The efficiency statistic is optimized, with a value of 0.69, and the temperature correction ΔT = -0.68°C. Daily average temperatures simulated using the lapse rate model and ΔT are lower on average than the measured temperature at Haig Glacier for summer 2007, 4.4°C and 5.2°C, respectively.
The lapse rate model was used to calculate daily average and maximum temperatures on the glacier for use in Eqn (5). Modelled PDD showed no significant bias to over- or underestimation (Fig. 3a and 4a). The average modelled PDD for 5 day periods in summer 2007 was 26°Cd, while the average of measured PDD was 24°C d.
Residual air temperature
Residual temperature, calculated from modelled air temperature and absorbed radiation as outlined above, is aggregated into residual PDD. The residual PDD are overestimated by the model (Fig. 3b and 4b). The average modelled and measured values for PDDres for 5 day periods in the 2007 season are 16.6 and 9.0°Cd. The highest error occurs in July, coinciding with the highest temperature errors and an extended period of underestimated incoming radiation.
Melt simulations
Modelled discharge is compared to discharge based on mass-balance surveys from 2004 and 2005 at Haig Glacier. The model underestimates total discharge by 1 7% and 2 1% in 2004 and 2005, respectively. A comparison experiment was made initializing the model with measured winter snowpack in both years. In these experiments, total runoff is underestimated by similar amounts, 1 8% and 2 1 % .
Modelled winter mass balance at the terminus of Haig Glacier is higher than measured for 2004, while at higher elevations snowpack is underestimated (Fig. 6a and b ). Initializing the model with estimated snowpack produces less melt at the terminus than model runs initialized with measured snowpack; while at higher elevations modelled snow produces more melt than measured v(Fig. 6c and d). The difference in accumulation between the measured and modelled simulations shows a similar spatial pattern to the difference in net balance between the two simulations, where underestimated accumulation corresponds to overestimates of melt and vice versa.
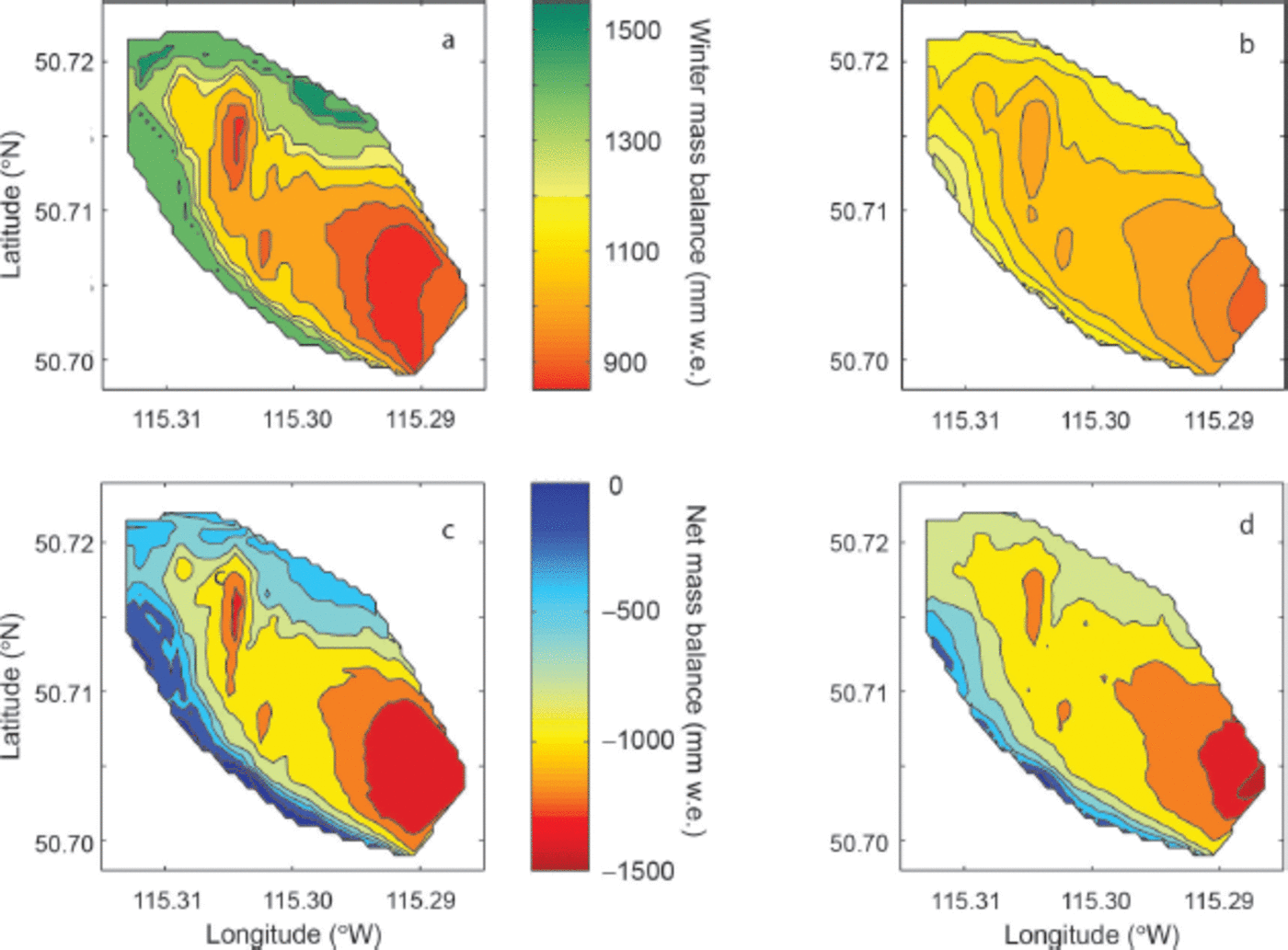
Fig. 6. (a, b) Winter mass balance (May snowpack; common colour bar) and (c, d) net mass balance (common colour bar) on Haig Glacier, 2003–04. (a, c) Measured data; (b, d) from the regional distributed model.
Given the close agreement between total runoff using two snowpack initializations in both 2004 and 2005, the over-and underestimations caused by the simplistic snowpack model used here balance out at Haig Glacier, at least for these two years. This relationship suggests that overall the model underestimates runoff, even when the error associated with initial snowpack is removed. This underestimation is in contrast to results reported above for 2007 where glacier melt is overestimated (Table 1).
The model is also run for the 1993–95 summer melt seasons for comparison to net balance at Peyto Glacier. In 1993 and 1994 the model underestimates net balance by 27% and 15%, respectively, whereas in 1995 it overestimates net balance by 5%. The large underestimation in 1993 is likely due to improper specification of initial snowpack, while modelled snowpack in 1994 and 1995 is closer to measured depths. The year-to-year pattern in modelled melt is consistent with what can be expected given the initial snowpack (i.e. more melt with less initial snow and vice versa). The correlation between melt and initial snowpack indicates the important role of albedo in affecting summer runoff, which is generally captured in the model.
Basin-Wide Glacial Melt
The distributed melt model is used to compute total glacial melt throughout the headwaters of the Bow River for the years 2000–09. The following analysis considers monthly discharge in Calgary and monthly ice melt.
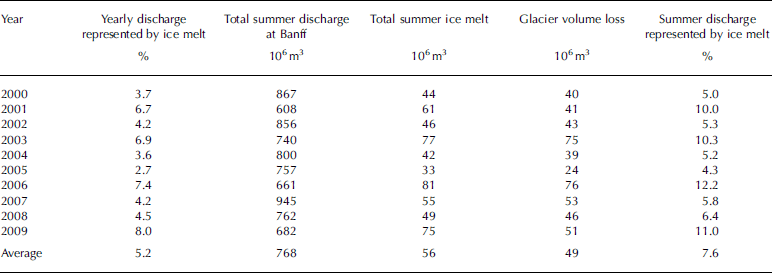
Table 2 summarizes summer (June–September) melt and discharge statistics for the years 2000–09. A monthly breakdown of glacial runoff reveals that the highest contribution from glacial ice melt comes in August (Table 3). The August contribution is two to nine times higher than that of July. We assume here that 100% of runoff is routed through the Bow River in the same month in which it melts. In reality, a portion of glacial runoff may be delayed through groundwater infiltration, and an additional amount may be lost due to evaporation.
Table 2. Estimated annual and summer (June–September) proportions of ice melt and basin yield for the Bow River at Calgary. The lowest basin yields and highest glacial melt are in boldface
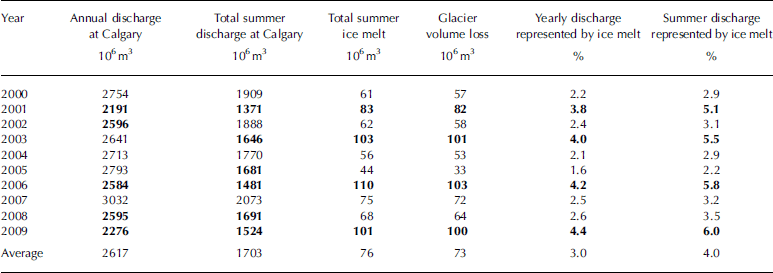
Table 3. Summary of glacier discharge breakdowns, 2000–09. Values above average are in boldface
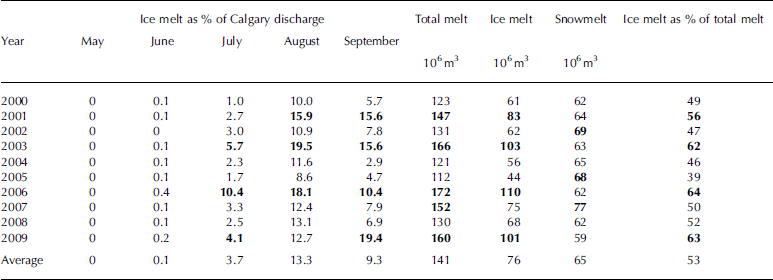
The four years with the lowest summer discharge in Calgary, 2001, 2003, 2006 and 2009, stand out as coinciding with three of the highest years of ice melt (Table 2; Fig. 7). These years also have the highest ratio of ice melt to total melt (Table 3). In these years ice melt represents 5.1–6.0% of summer discharge in Calgary. September ice melt in 2009 is considerably higher than in other years and shows a higher contribution to streamflow than July and August of the same year (Fig. 7).
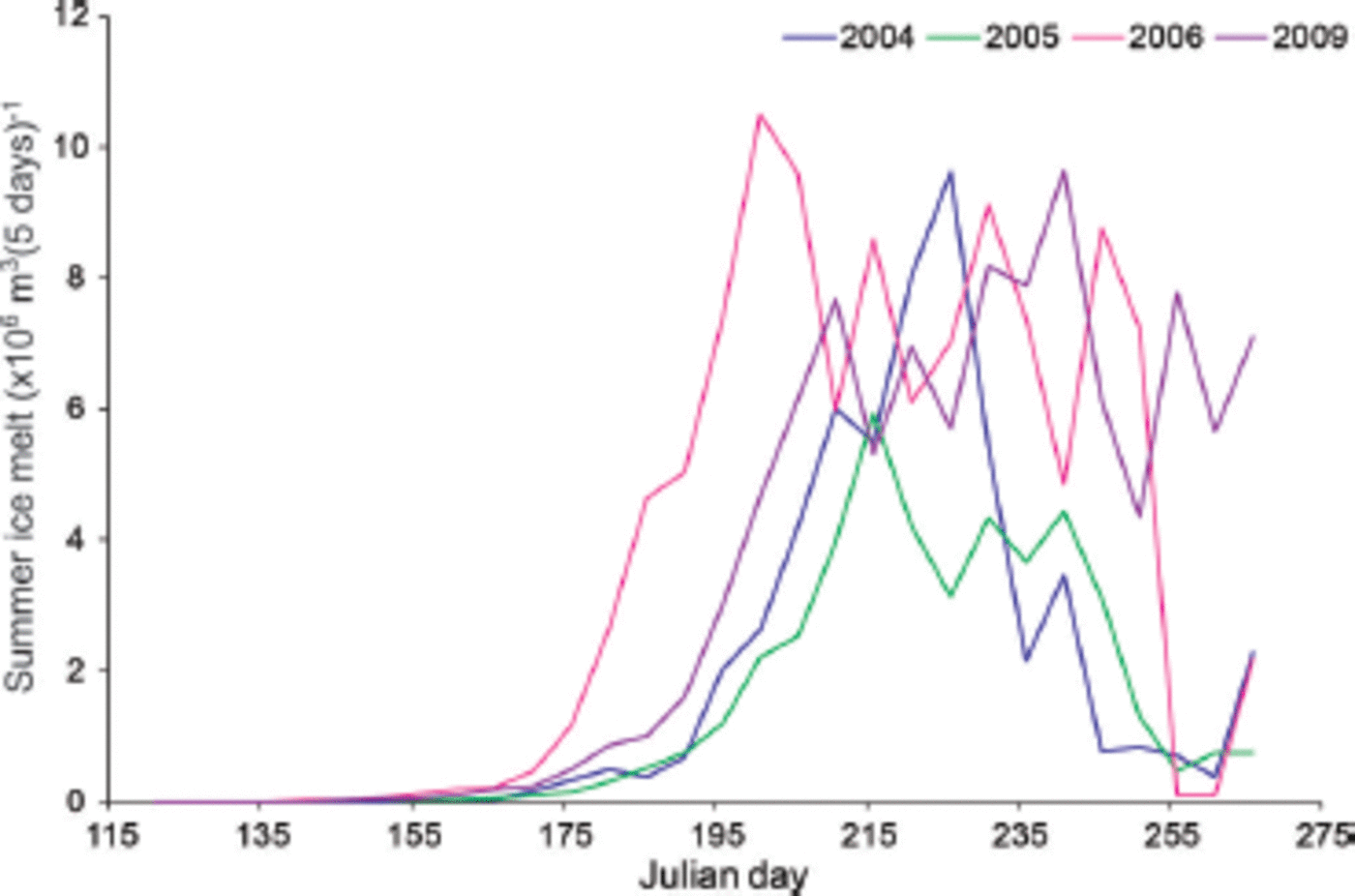
Fig. 7. Summer ice melt for selected years of high and low melt, 2004–06 and 2009.
In 2006, ice melt represents a significant portion of the total annual flow in Calgary, 4.2%, as well as one of the highest August contributions to Calgary discharge. Peak discharge in Calgary was 3–4 weeks earlier than on average, during the last week of May and first week of June (Fig. 8). During 2006, August flow in Calgary was 82% of the average August flow for the decade. Lower flows lead to an especially high glacial contribution in July, August and September of that year. In contrast, 2005 ice melt contributes only 1.6% of annual discharge at Calgary. In that year, total ice melt is less than half of the 2006 total, while total summer discharge in Calgary was 5% greater than in 2006.
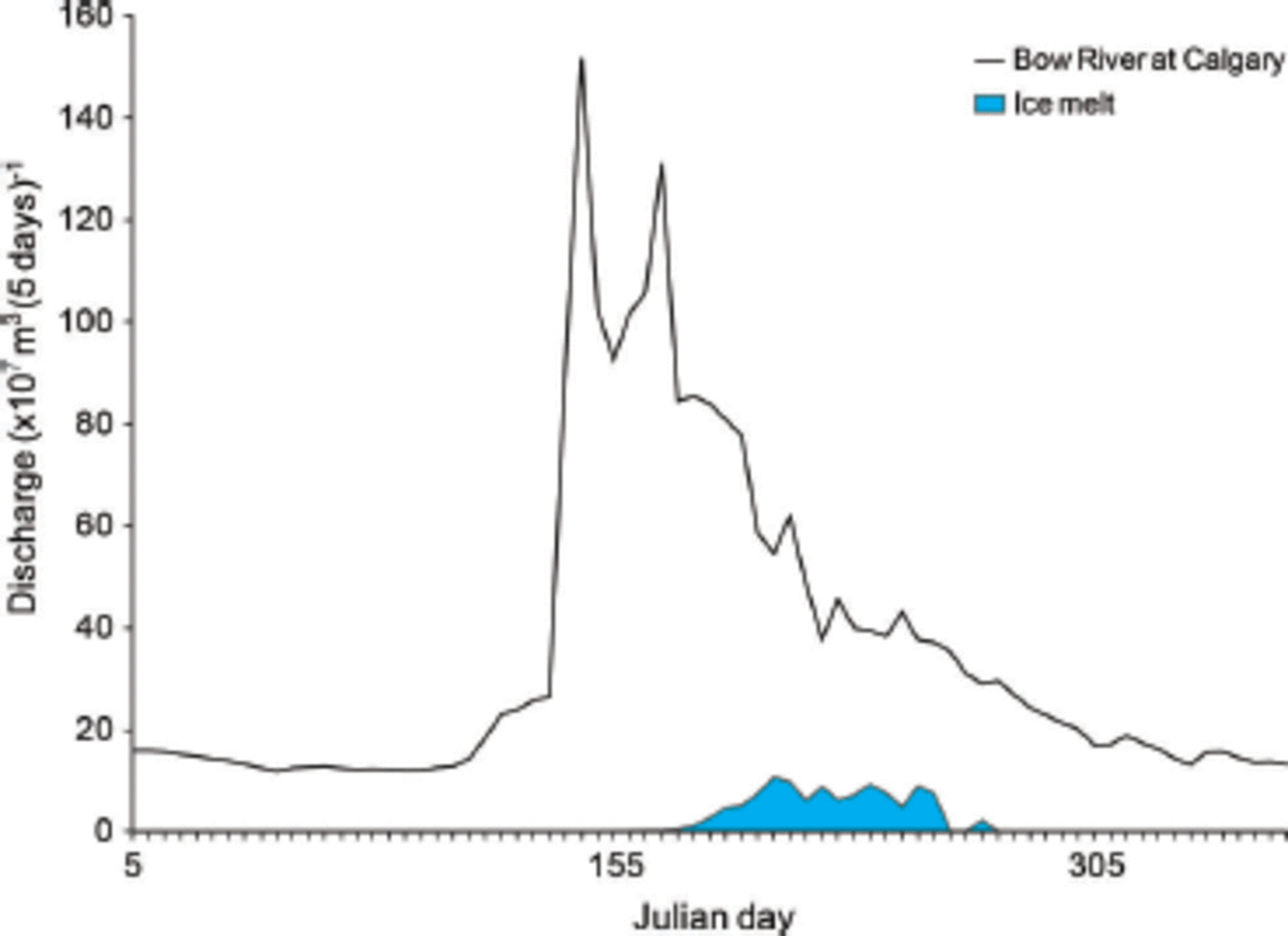
Fig. 8. Ice melt and Bow River discharge at Calgary for 2006. This is the year of highest melt between 2000 and 2009.
For comparison with discharge reported in Reference Hopkinson and YoungHopkinson and Young (1998), a brief summary of modelled summer (June–September) discharge from glaciers above Banff is given in Table 4. In this table and Table 2, glacier volume change (i.e. net mass balance) is included for better comparison with previous studies. In years of negative net balance, net mass balance and ice melt are similar (<10% difference), except in the case of 2005. Unusually high summer snowfall in 2005 contributes to a less negative net balance in that year.
Table 4. Estimated annual proportions of ice melt and basin yield for the Bow River in Banff
Discussion
Model performance
The model developed in this study is able to remove the high collinearity between absorbed radiation and air temperature. When the residual temperature is used in Eqn (7), the resultant model explains 71% of variability in melt at the AWS on Haig Glacier, based on 5 day melt periods. Model performance is equivalent to that of a radiation-temperature melt model based on Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005). Both models under-predict the total melt at the weather station by -10% when tested against observed data from 2007, with average errors of ~30% for 5 day melt totals (Table 1).
This method is of most use in areas where degree-day factors are highly variable over small scales, such as valley glaciers in complex mountain environments. Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005) address these issues, but their modelling approach fails to account for collinearity of the two independent variables, temperature and absorbed radiation. The presence of collinearity can inflate variance in regression coefficients, which introduces higher uncertainty into model predictions (Reference StewartStewart, 1987). In fact, in the presence of collinearity, least-squares regression is no longer the best linear unbiased estimator. This stems from the shared information provided by both variables, which cannot easily be separated to provide two distinct relationships with the predictand (Reference Belsley, Kuh and WelschBelsley and others, 2004).
In light of this, the model provided in this study is an advance because it is able to separate the influence of each variable. In cases where a complete energy balance is not feasible, the model presented here may be a good choice. The required inputs are readily available and the distributed model is physically based and easily interpreted, making it portable to other areas.
Modelled runoff
Results of modelling from the past decade are comparable to previous work examining glacial runoff in the Bow River basin, which is summarized in Table 5. The three basin-scale studies have estimates of glacier area ranging from 60 to 89 km2. We calculate 57km2 of ice based on satellite imagery from the period 2004–06 (Reference Bolch, Menounos and WheateBolch and others, 2010), including all ice bodies greater than 0.1 km2.
Table 5. Summary of Bow basin glacier studies
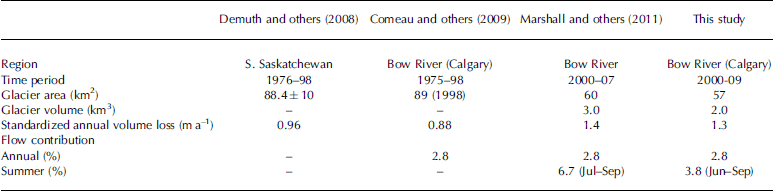
For comparison between studies, annual glacial volume loss is standardized by the total glacial coverage (km2). Annual melt contributions to the basin reported in the literature for the late 20th century range from 0.88 to 1.4 m a–1. The contribution calculated in this study 1.3 m a–1 on average, is closest to the melt calculated by Reference MarshallMarshall and others (2011). The lower average contribution reported by Reference Demuth and BonardiDemuth and others (2008) and Reference Comeau, Pietroniro and DemuthComeau and others (2009) may be attributed to different periods of study; glacier mass balance in the region was more negative in the 2000s than in earlier periods.
Relative contributions in summer are lower in this study than reported by Reference MarshallMarshall and others (2011), but it should be noted that direct comparison of estimates provided in these studies is complicated by varying definitions of the summer melt season. In this study, melt from June to September is included in estimates and compared to streamflow from the same period, while other studies report summer percentages as July-September. When June ice melt is excluded, the average summer contribution from ice melt is 75x106m3, equivalent to 7.4% of July-September discharge in Calgary.
Average contributions to the Bow River above Banff are significantly higher than estimates provided by Reference Hopkinson and YoungHopkinson and Young (1998), Reference Demuth and BonardiDemuth and others (2008) and Reference Comeau, Pietroniro and DemuthComeau and others (2009) (Table 6). Reference Hopkinson and YoungHopkinson and Young (1998) provide a breakdown showing annual glacier contributions to the river ranging from -3.7% to 13.2%, where negative percentages indicate years of positive net balance. In the early period of the study, the authors show more glacier storage than depletion, but from 1980 to 1993 the average contribution is 3.6%. For the same period they report average annual glacier volume losses of 42:3 x 106 m3 a–1. This is more comparable to the average ice melt we have calculated in this study, 48:7 x 106m3. Reference Demuth and BonardiDemuth and others (2008) and Reference Comeau, Pietroniro and DemuthComeau and others (2009) do not provide an annual breakdown, so it is difficult to compare directly with our estimates.
Table 6. Summary of studies of glaciers above Banff
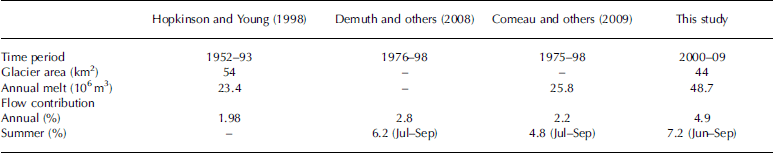
In the past decade the highest ice melt coincided with years with low discharge in Calgary. In these years the proportion of annual and summer discharge attributed to ice melt is high. Reference Hopkinson and YoungHopkinson and Young (1998) found similar results between 1952 and 1993. The concurrency of low total discharge and high glacial melt ties in with the relationship between snowfall and mass balance discussed above, and is related to the persistence of warm, dry high-pressure ridging events in these summers. Such weather systems give both reduced summer precipitation and increased glacier melt. In a snowmelt-dominated river such as the Bow, low winter snowpack means low river flows. These years commonly correspond to years of especially high ice melt on the glacier, leading to the increased percentage contribution to streamflow.
September 2009 serves as a good example of the limitations of running the model only from May through September. In that year, September discharge is exceptionally high and melt does not shut off by the end of the month. Field visits in late September that year revealed exposed ice over the entire glacier surface at Haig Glacier. While this pattern is atypical during the study period, it will likely become more common in the future and this pattern should be taken into consideration when modelling glacier runoff. This problem is easily solved by running the model for the full year, allowing accumulation and melt to be determined by temperatures, rather than arbitrary calendar dates.
Representativeness of field calibration sites
We assume that climatological conditions and mass-balance processes at Haig and Peyto Glaciers are representative of the Bow basin. This is difficult to confirm without additional field data, as no meteorological or glaciological data are available from other glaciers in the basin. From available data, though, there is no reason to believe that either Haig or Peyto Glacier is climatically unusual. They are near the southern and northern edges of the basin, bracketing most of the other ice masses. Each glacier has an accumulation area on the continental divide, along with median elevations and aspects that are representative of glaciers in the Bow basin. Snow accumulation totals are similar at each site, with average specific winter balances of B w = 1195 ± 290 mm w.e. at Peyto Glacier (1966-95; Reference Demuth, Keller, Demuth, Munro and YoungDemuth and Keller, 2006) and B w = 1320 ±295 mm w.e. at Haig Glacier (2002-13; unpublished data). Data periods do not overlap, unfortunately, but this constitutes all available winter mass-balance data at the two sites. Peyto Glacier is not anomolously snowy for the region, despite its size. Rather, glaciers within the basin are concentrated in the continental divide region, where they exist due to the high snow accumulations delivered by moist Pacific air masses that intersect the Rocky Mountains.
We assume that summer melt-season processes work the same way throughout the basin, based on the Haig Glacier model calibration. Because the melt model is physically based, and solar radiation can be modelled as a function of local terrain, we argue this is a reasonable assumption, but we are not able to test it with available data. One of the main uncertainties is whether albedo values at Haig Glacier are representative of other glaciers in the basin. Published snow and ice albedo values for Peyto Glacier are similar to those at Haig Glacier (Reference Cutler and MunroCutler and Munro, 1996), supporting our assumption that the Haig Glacier melt model is portable within the basin. A second question is whether the summer temperature regime and temperature lapse rates in the atmospheric boundary layer at Haig Glacier are representative. Katabatic winds on larger glaciers, such as Peyto, cause cooling at lower elevations in these environments, and other local terrain effects (e.g. shading) affect summer temperature. Katabatic winds are weak and intermittent at Haig Glacier and are drowned out by topographic funnelling of synoptic-scale winds, which are frequently strong. Because most glaciers in the Bow basin are smaller than Haig Glacier and in similar meteorological and topographic environments, this may make it a suitable reference site. Additional field data are needed to examine this.
Model uncertainties
The melt model is nonlinear, and multiple sources of error propagate through the model, including uncertainties in the initial snow depth, near-surface air temperature, albedo, and incoming solar radiation (with errors primarily due to poor estimation of cloud cover/effective atmospheric transmissivity). These errors are mutually dependent; for instance, error in the initial snow depth leads to improper albedo evolution (transition from snow to ice), which affects absorbed radiation and, in turn, the residual temperature calculation. It is therefore difficult to isolate the error arising from each component of the model, but we can assess the overall model performance for Haig and Peyto Glaciers through comparison with summer mass-balance data. This provides an estimate of the ‘bottom line’ in terms of model errors and biases.
Based on this approach, a negative bias is evident in the melt model (tendency to underestimate summer melt), and modelled summer mass balance for individual years has an error of up to 27%. For the years that we test, two melt seasons on Haig Glacier and three on Peyto Glacier, total summer melt is underestimated for four summers (average of 20%) and overestimated for one (+5%), giving a mean bias of –15%. Haig Glacier simulations with in situ vs far-field (‘degraded’) model inputs indicate that modelled temperature and incoming solar radiation are both significant sources of error. For our calibation period (summer 2007), modelled incoming solar radiation is only 82% of observed, and mean modelled temperature is 0.8°C too low. Both of these influences contribute to the model bias.
Snow depth and estimated cloud cover stand out as the two greatest sources of uncertainty in modelled variables, as they both affect the amount of absorbed radiation at the surface. Model runs at Peyto and Haig Glaciers highlight the sensitivity of the model to initial snowpack conditions. Two effects can be seen from differences in initial snowpack: an influence on glacier mass balance and the influence on albedo.
Higher winter snowpack leads to more positive mass balance and hence less ice melt contributing to river flows. With a higher snowpack, ice is exposed later in the summer than when winter snowpack is lower. In these years, shorter ice exposure before the onset of new snow cover decreases the total amount of melt contributing to the river. Conversely, when winter snowpack is low, low-albedo ice is exposed longer. With winter balance already being lower in these years, increases in melt push net balance even lower. Simulations at Haig and Peyto Glaciers show the greatest discrepancy between measured and modelled melt in years when snowpack is greatly overestimated, particularly at the terminus (i.e. 2005 and 1993, respectively). In 2007, modelled snowpack at Haig Glacier AWS is only marginally higher than measured, 90 mm w.e. In these model runs, albedo estimates closely track with measured albedo and melt is overestimated by 4%.
The performance of the model at the distributed scale is limited by a simplistic snowpack model. The model underestimates winter mass balance at both Haig and Peyto Glaciers, with a mean bias of –291 and –50mmw.e. respectively. As discussed above, this underestimation tends to inflate modelled melt through longer ice exposure. The model is also unable to capture snow distribution patterns seen at Haig Glacier (Fig. 5). In order to improve model accuracy, a distributed snowpack model for the region should be incorporated. Variability in snow distribution is highly dependent on local winds, orographic lifting and air moisture content (Reference ListonListon, 2004). While the model used here attempts to capture the general increase in snowpack with elevation, snow redistribution due to wind is not accounted for. Moreover, our reference station, Banff, is on the lee side of the Rocky Mountains, where it is much drier; the high-mountain snowpack in the region is influenced by the westerly air masses that deliver orographic precipitation on the windward slopes and on the continental divide. We recommend that in future work the upslope precipitation process should be physically modelled, along with wind transport and redistribution, to improve on the glacier snowpack model. Regional-scale meteorological models or linearized orographic precipitation models (e.g. Reference Smith and EvansSmith and Evans, 2007; Reference Jarosch, Anslow and ClarkeJarosch and others, 2012) are both potentially viable ways to model snowpack in more detail. The importance of wind redistribution can be seen in snow accumulation patterns at Haig Glacier, which are similar and nonlinear year after year. Regional blowing-snow models are not available yet, but catchment-scale models have been tested (e.g. Reference Winstral, Elder and DavisWinstral and others, 2002; Reference MacDonald, Pomeroy and PietroniroMacDonald and others, 2009). Reference Winstral, Elder and DavisWinstral and others (2002) found snow accumulation at a catchment scale is better predicted by the addition of upwind topographic characteristics, such as degree of exposure and slope breaks, to more commonly used parameters of slope, elevation and radiation input. These models have yet to be tested at larger scales.
Modelling incoming solar radiation based on a cloud factor is also problematic for model performance; introduction of NCEP cloud cover reduces incoming radiation by 18% at the Haig Glacier AWS compared to radiation modelled using local cloud cover estimates. Cloud formation is a complex interaction of many meteorological variables, which are difficult to model regionally or to assess from satellite imagery at the temporal and spatial scales of alpine glacier energy-balance modelling. In addition to cloud coverage, the type and height of cloud has varying effects on shortwave radiation reaching the ground (i.e. high clouds absorb less radiation than lower clouds). This distinction is not captured in the NCEP data, which are a total cloud cover fraction. A high-resolution meteorological model or a high-density monitoring network are likely the only ways to accurately capture cloud cover. These are both impractical solutions for regional modelling, however. The only current options are statistical treatments of cloud cover, which are effectively similar to what we implement here, or parameterizations based on measured variables such as daily temperature range (Reference Dai, Trenberth and KarlDai and others, 1999). Average summer cloud conditions appear to be reasonably captured with NCEP cloud cover, but detailed hourly and daily conditions are poorly simulated. Satellite imagery could be helpful for historical mass-balance and melt modelling, but we are interested in developing methods that can be applied to future forecasts, using, for example, large-scale cloud conditions from climate models.
One fortuitous feature of the model is that there is a builtin ‘buffer’ (negative feedback) in the propagation of errors associated with absorbed solar radiation. Underestimates of absorbed solar radiation give residual temperature values that are too high, since T res ≈ T - βI abs. Hence, PDDres estimates are too high when I abs is too low; this is a compensating error, such that the estimated melt, MF • PDDres + RF • I abs, has less error than that of I abs, and possibly a different sign. In the case above, for instance, PDDres is 84% too high (Table 1), despite lower temperatures, and modelled melt at the AWS site is 4% more than observed. This systematic compensation means that errors in cloud cover and albedo are buffered rather than amplified, although it leads to the concern that reasonable model performance can mask serious errors in input data or model parameters.
Overall, our model experiments indicate that the combined error in the snowpack and melt modelling is about -15%, with the negative bias indicating that we underestimate total summer melt. Errors for individual melt seasons range from -27% to 5%. There is negligible bias in modelled summer melt at the Haig Glacier AWS site, where the model was calibrated, but errors in 5 day melt totals at the AWS site are ±30%.
Conclusions and Future Work
The model developed in this study improves on the work of Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005) by addressing the collinearity between air temperature and absorbed radiation in the glacier boundary layer. Without this improvement, linear combinations of temperature and radiation may result in unstable models and high sensitivity to data subset selection.
There is room for improvement in modelling the statistical relationship between temperature and absorbed radiation, but the uncertainties in this regression are probably minor compared with the larger uncertainties associated with modelling of the initial snowpack, albedo, and cloud cover. Tested against field data from summer 2007 at the Haig Glacier AWS site, the model simulates 5 day melt totals reasonably well (N = 0.65), with a total error of 10% over the melt season. Applied to the entire glacier in two other melt seasons, 2004 and 2005, the distributed melt model underpredicts melt by 20%. We find similar estimates of model accuracy when predicted melt is compared with available summer mass-balance data from Peyto Glacier. Accuracy is degraded through the introduction of the regional-scale climate forcing, which uses NCEP cloud cover, particularly for short-term (i.e. daily) melt modelling, but the regional model works well for predictions of total melt-season runoff in the historical period.
The model is limited by a simplistic method of modelling snow accumulation. Total melt is highly sensitive to initial snowpack as well as summer snowfall timing. A realistic estimate of winter snow accumulation and a realistic derivation of summer snowfall from global climate model predictions are critical for accurate future melt estimates. Despite potential drawbacks, the model performs reasonably well in reconstructing past melt at Haig Glacier. Application of the model to two widely separated glaciers, Peyto and Haig, demonstrates the portability of the model and its utility in regional-scale modelling. In light of runoff estimates that are similar to those of other studies of glaciers in the Bow River, we believe the model is able to accurately estimate basin-scale runoff.
Average modelled ice melt from glaciers in the Bow River basin from the past decade is 76 x106m3a–1. Ice melt accounts for 4.0% of summer discharge in Calgary on average, but reaches 5.8% in 2006. The same year, glacial ice melt was equivalent to 18% of discharge in the Bow River at Calgary during August, and flows in Calgary were 18% lower than average. On average for the period 2000-09, we estimate that glacier runoff due to melting ice and firn contributes 13% to the Bow River runoff in Calgary in August. September contributions are also high, 9% on average. This is the runoff associated with melting of glacier ice; on average, this represents -50% of the total runoff from glaciers, but most of the runoff in the early melt season (May-July) is associated with the seasonal snowpack. These values support previous studies, which have found glacial melt contributions to be most important in late summer and years of low total flow. The findings of this and other studies of the Bow River basin show the importance of glaciers as reservoirs in mountain environments.
Future work will focus on projecting glacial melt volume into the coming century by coupling the melt model with a dynamic model of glacier evolution.
Acknowledgements
We thank the Natural Sciences and Engineering Research Council (NSERC) of Canada for support of the field studies at Haig Glacier. The University of Calgary and the Western Canadian Cryospheric Network, funded by the Canadian Foundation for Climate and Atmospheric Sciences, provided graduate support to E. Bash. We are grateful to S. Adhikari for his input to the manuscript. We thank the two anonymous reviewers and the associate editor, D. MacAyeal, for helpful insights and suggestions.
















