1. Introduction
Correlation among assets plays an important role in the financial market. Empirical evidence shows that market returns are lower when correlations among assets are increasing, since higher correlations reduce the diversification effect and increase the market volatility. Roughly stated, the correlation risk premium (CRP) is the difference between the realized and the option-implied, i.e., risk-neutral correlation.Footnote 1 The CRP can be interpreted as an insurance premium paid for assets that hedge against unanticipated rises in correlation. Academic research has provided more empirical evidence to show that the CRP in equity markets is economically and statistically significant and long-term market returns can be predicted using the option-implied correlation; see, e.g., Driessen et al. (Reference Driessen, Maenhout and Vilkov2009), Faria & Kosowski (Reference Faria and Kosowski2014), Buss et al. (Reference Buss, Schönleber and Vilkov2017), and Faria et al. (Reference Faria, Kosowski and Wang2022). In this paper, we will provide a theoretical framework that allows to better understand the CRP.
Stocks and market indices are modeled as random variables on the probability space
![]() $\left ( \Omega, \left ( \mathcal{F}_t\right ) _{t\geq 0},\mathbb{P}\right )$
. Under the assumption of no-arbitrage, the prices of traded derivatives can be expressed as discounted expected payoffs under a risk-neutral probability measure
$\left ( \Omega, \left ( \mathcal{F}_t\right ) _{t\geq 0},\mathbb{P}\right )$
. Under the assumption of no-arbitrage, the prices of traded derivatives can be expressed as discounted expected payoffs under a risk-neutral probability measure
![]() $\mathbb{Q}$
. Implied correlations (i.e., the correlation between assets under the risk neutral measure) can be determined from traded derivative prices, as was shown in Skintzi & Refenes (Reference Skintzi and Refenes2004). Indeed, implied correlation provides a measure of the relative cheapness/richness of index options in relation to the index components, see, e.g., Chicago Board Options Exchange (2022). It reveals in the first place information about the degree of the comovement under the probability measure
$\mathbb{Q}$
. Implied correlations (i.e., the correlation between assets under the risk neutral measure) can be determined from traded derivative prices, as was shown in Skintzi & Refenes (Reference Skintzi and Refenes2004). Indeed, implied correlation provides a measure of the relative cheapness/richness of index options in relation to the index components, see, e.g., Chicago Board Options Exchange (2022). It reveals in the first place information about the degree of the comovement under the probability measure
![]() $\mathbb{Q}$
, see also Dhaene et al. (Reference Dhaene, Linders, Schoutens and Vyncke2012), Linders et al. (Reference Linders, Dhaene and Schoutens2015), and Madan & Schoutens (Reference Madan and Schoutens2013) for alternative implied dependence measures. The discrepancy between the realized correlation (i.e., the correlation between assets under the real-world measure
$\mathbb{Q}$
, see also Dhaene et al. (Reference Dhaene, Linders, Schoutens and Vyncke2012), Linders et al. (Reference Linders, Dhaene and Schoutens2015), and Madan & Schoutens (Reference Madan and Schoutens2013) for alternative implied dependence measures. The discrepancy between the realized correlation (i.e., the correlation between assets under the real-world measure
![]() $\mathbb{P}$
) and the implied correlation gives rise to the existence of the CRP.
$\mathbb{P}$
) and the implied correlation gives rise to the existence of the CRP.
The increasing complexity of insurance products has introduced the need to understand the difference between implied and real-world correlation when dealing with insurance problems. Indeed, modern insurance products combine actuarial and financial risks. Therefore, their valuation and risk management rely on real-world and risk-neutral probabilities. For example, Solvency II requires that insurance companies value their liabilities in a “fair’” way, which implies that risk-neutral valuation has to be used for financial risks and real-world valuation for the actuarial risks. See, for example, Pelsser & Stadje (Reference Pelsser and Stadje2014), Ghalehjooghi & Pelsser (Reference Ghalehjooghi and Pelsser2020), Dhaene et al. (Reference Dhaene, Stassen, Barigou and Chen2017), Barigou et al. (Reference Barigou, Chen and Dhaene2019), and Linders (Reference Linders2023) for various methodologies for pricing insurance products based on combinations of real-world and risk-neutral information. Examples of complex insurance products combining financial and actuarial risks are variable annuities. In Bauer et al. (Reference Bauer, Kling and Russ2008) and Bacinello et al. (Reference Bacinello, Millossovich, Olivieri and Pitacco2011), a valuation framework for a general class of variable annuities based on risk-neutral and real-world expectations was introduced. Concrete examples are then provided in Coleman et al. (Reference Coleman, Kim, Li and Patron2007), Feng & Jing (Reference Feng and Jing2017), and MacKay et al. (Reference MacKay, Vachon and Cui2023). Therefore, understanding the difference between risk-neutral and real-world information is important when considering variable annuities.
In this paper, we consider a discrete market setting. For stochastic finance in discrete time, one can refer to Föllmer & Schied (Reference Föllmer and Schied2004). We investigate to what extent the implied correlation reveals information about the degree of the comovement under the probability measure
![]() $\mathbb{P}$
. We illustrate how statements which hold true in the risk-neutral world do not necessarily hold in the real world. For example, stock prices can be strongly negative dependent in the risk-neutral world (under
$\mathbb{P}$
. We illustrate how statements which hold true in the risk-neutral world do not necessarily hold in the real world. For example, stock prices can be strongly negative dependent in the risk-neutral world (under
![]() $\mathbb{Q}$
) while being positive dependent in the real world (under
$\mathbb{Q}$
) while being positive dependent in the real world (under
![]() $\mathbb{P}$
), this leads to a large difference between the real-world and the risk-neutral correlation, which is quantified by the correlation gap. Moreover, we introduce a new derivative called dispersion swap to trade the correlation gap and demonstrate that the correlation gap does not converge to zero for market equilibrium, i.e., the realized correlation can be different with the implied correlation in the case of market equilibrium.
$\mathbb{P}$
), this leads to a large difference between the real-world and the risk-neutral correlation, which is quantified by the correlation gap. Moreover, we introduce a new derivative called dispersion swap to trade the correlation gap and demonstrate that the correlation gap does not converge to zero for market equilibrium, i.e., the realized correlation can be different with the implied correlation in the case of market equilibrium.
In Section 2, we introduce a simple discrete financial market with two traded stocks. We apply the multivariate binomial tree model for the underlying stock prices. At time
![]() $t,$
$t,$
![]() $t=0, 1, 2\dots, $
the price of the stock at the next valuation moment
$t=0, 1, 2\dots, $
the price of the stock at the next valuation moment
![]() $t+1$
can only take two possible outcomes. This financial market is arbitrage-free and incomplete, we characterize the set of feasible risk-neutral probability measures and demonstrate that it is feasible to determine a risk-neutral measure
$t+1$
can only take two possible outcomes. This financial market is arbitrage-free and incomplete, we characterize the set of feasible risk-neutral probability measures and demonstrate that it is feasible to determine a risk-neutral measure
![]() $\mathbb{Q}$
by explicitly specifying the implied correlation. Note that we limit our analysis to two stocks in the financial market. This choice is motivated by the fact that a market with two assets offers an intuitive setting for both theoretical and numerical exploration of the correlation gap.Footnote
2
$\mathbb{Q}$
by explicitly specifying the implied correlation. Note that we limit our analysis to two stocks in the financial market. This choice is motivated by the fact that a market with two assets offers an intuitive setting for both theoretical and numerical exploration of the correlation gap.Footnote
2
In Section 3, we consider the situation where a pricing measure is chosen by the market from the set of feasible risk-neutral probability measures, see Section 3.1. We show that the pricing measure chosen by the market can differ substantially from the real-world probability measure without introducing arbitrage opportunities. We give an example where the dependence structure used to price multivariate derivatives is different from the real-world dependence structure. In such a situation there can be a significantly large correlation gap in the financial market, i.e., the difference between risk-neutral and real-world correlations is substantial.
In Section 4, we consider the sale of a unit-linked insurance product to a group of
![]() $N$
policyholders. The payoff of this unit-linked contract is contingent upon the performance of a stock market fund comprising two stocks within the financial market. We demonstrate how disparities between real-world dependence and risk-neutral dependence contribute to determining the expected excess return above the risk-free return for each policyholder. To be more specific, an example is presented in Section 4.1 to illustrate that the expected excess return for the purchase of the unit-linked insurance is determined by the correlation gap. A nonzero correlation gap leads to a nonzero expected excess return for buying the unit-linked insurance product. Therefore, policyholders of the unit-linked insurance product are also facing the correlation risk in the financial market.
$N$
policyholders. The payoff of this unit-linked contract is contingent upon the performance of a stock market fund comprising two stocks within the financial market. We demonstrate how disparities between real-world dependence and risk-neutral dependence contribute to determining the expected excess return above the risk-free return for each policyholder. To be more specific, an example is presented in Section 4.1 to illustrate that the expected excess return for the purchase of the unit-linked insurance is determined by the correlation gap. A nonzero correlation gap leads to a nonzero expected excess return for buying the unit-linked insurance product. Therefore, policyholders of the unit-linked insurance product are also facing the correlation risk in the financial market.
At first, a large correlation gap may look like a dysfunction of the financial market. However, we propose in Section 5 that, in our simple market model, one can use a new derivative, the dispersion swap, to exploit the correlation gap. This strategy is not an arbitrage strategy, but as dependence under
![]() $\mathbb{Q}$
is moving further and further away from its
$\mathbb{Q}$
is moving further and further away from its
![]() $\mathbb{P}$
counterpart, buying the dispersion swap becomes more attractive in terms of larger expected profit. To be more precise, a large positive correlation gap, corresponding to the situation that the realized correlation is expected to exceed the implied correlation, results in a significant positive expected profit for longing the dispersion swap. Furthermore, we show how one can combine the floating leg of individual variance swaps and the floating leg of the index variance swap to approximate the floating leg of the dispersion swap, which is called the realized dispersion. The expected profit for a buyer of the dispersion swap is directly related to the correlation gap, the higher this gap, the higher the expected profit. The idea of setting up trading strategies to exploit the difference between realized and implied dependence was also discussed in Laurence (Reference Laurence2008), Laurence & Wang (Reference Laurence and Wang2008), Bossu (Reference Bossu2014), and Meissner (Reference Meissner2015).
$\mathbb{P}$
counterpart, buying the dispersion swap becomes more attractive in terms of larger expected profit. To be more precise, a large positive correlation gap, corresponding to the situation that the realized correlation is expected to exceed the implied correlation, results in a significant positive expected profit for longing the dispersion swap. Furthermore, we show how one can combine the floating leg of individual variance swaps and the floating leg of the index variance swap to approximate the floating leg of the dispersion swap, which is called the realized dispersion. The expected profit for a buyer of the dispersion swap is directly related to the correlation gap, the higher this gap, the higher the expected profit. The idea of setting up trading strategies to exploit the difference between realized and implied dependence was also discussed in Laurence (Reference Laurence2008), Laurence & Wang (Reference Laurence and Wang2008), Bossu (Reference Bossu2014), and Meissner (Reference Meissner2015).
Apart from trading the dispersion swap to make a profit, investors can also long the dispersion swap to hedge against unanticipated correlation spikes in the financial market. Because the investors may have a high degree of risk aversion towards the correlation risk, they are willing to buy the dispersion swap, even with a negative expected profit. The expected profit of a dispersion swap is also called the CRP, as it represents the price that market participants are willing to pay to sell correlation risk. On the other hand, we show that the dispersion swap with a strictly negative (or positive) expected return is not an arbitrage strategy. Therefore, we conclude in Section 6 that a market in equilibrium can accommodate a negative CRP.
2. The financial market
2.1 A discrete financial market
We consider a discrete financial market with two nondividend paying stocks over a finite time horizon. Today is time
![]() $0$
, the price of stock
$0$
, the price of stock
![]() $i$
$i$
![]() $(i = 1 \text{ or } 2)$
, at the future time
$(i = 1 \text{ or } 2)$
, at the future time
![]() $t$
(
$t$
(
![]() $t=1,2,\ldots, n$
), is denoted by
$t=1,2,\ldots, n$
), is denoted by
![]() $S_i(t)$
.Footnote
3
Given the price of stock
$S_i(t)$
.Footnote
3
Given the price of stock
![]() $i$
at time
$i$
at time
![]() $t-1$
, the future stock price at time
$t-1$
, the future stock price at time
![]() $t$
can only increase to
$t$
can only increase to
![]() $e^{u_{i}}S_{i}(t-1)$
or decrease to
$e^{u_{i}}S_{i}(t-1)$
or decrease to
![]() $e^{d_{i}}S_{i}(t-1)$
. The forward return of stock
$e^{d_{i}}S_{i}(t-1)$
. The forward return of stock
![]() $i$
at time
$i$
at time
![]() $t$
is denoted by
$t$
is denoted by
![]() $R_{i}(t)$
and defined as:
$R_{i}(t)$
and defined as:
The financial market is also home to a bank account, which allows borrowing and lending at a constant, risk-free interest rate
![]() $r$
. The time
$r$
. The time
![]() $0$
value of the risk-free asset is
$0$
value of the risk-free asset is
![]() $B(0)$
, and its time
$B(0)$
, and its time
![]() $t$
value is given by
$t$
value is given by
![]() $B(t) = e^{rt}B(0)$
. We assume that
$B(t) = e^{rt}B(0)$
. We assume that
![]() $e^{u_{i}}$
and
$e^{u_{i}}$
and
![]() $e^{d_{i}}$
are symmetric with respect to the forward rate
$e^{d_{i}}$
are symmetric with respect to the forward rate
![]() $e^r$
:
$e^r$
:
Under the real-world probability measure
![]() $\mathbb{P}$
, we denote the joint probabilities of the random vector
$\mathbb{P}$
, we denote the joint probabilities of the random vector
![]() $\left ( R_{1}(t),R_{2}(t)\right )$
as follows:
$\left ( R_{1}(t),R_{2}(t)\right )$
as follows:
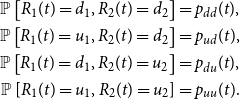 \begin{align} \mathbb{P}\left [ R_{1}(t)=d_1,R_{2}(t)=d_2 \right ] & =p_{d d}(t),\nonumber\\ \mathbb{P}\left [ R_{1}(t)=u_1,R_{2}(t)=d_2\right ] & =p_{u d}(t),\nonumber \\ \mathbb{P}\left [ R_{1}(t)=d_1,R_{2}(t)=u_2\right ] & =p_{d u}(t),\nonumber \\ \mathbb{P}\left [ R_{1}(t)=u_1,R_{2}(t)=u_2 \right ] & =p_{u u}(t). \end{align}
\begin{align} \mathbb{P}\left [ R_{1}(t)=d_1,R_{2}(t)=d_2 \right ] & =p_{d d}(t),\nonumber\\ \mathbb{P}\left [ R_{1}(t)=u_1,R_{2}(t)=d_2\right ] & =p_{u d}(t),\nonumber \\ \mathbb{P}\left [ R_{1}(t)=d_1,R_{2}(t)=u_2\right ] & =p_{d u}(t),\nonumber \\ \mathbb{P}\left [ R_{1}(t)=u_1,R_{2}(t)=u_2 \right ] & =p_{u u}(t). \end{align}
We assume that the joint probabilities under real-world measure
![]() $\mathbb{P}$
are strictly positive. The distribution of the random vector
$\mathbb{P}$
are strictly positive. The distribution of the random vector
![]() $\left ( R_{1}(t),R_{2}(t)\right )$
is determined by the marginal distributions of
$\left ( R_{1}(t),R_{2}(t)\right )$
is determined by the marginal distributions of
![]() $R_{i}(t),$
and the dependence structure connecting
$R_{i}(t),$
and the dependence structure connecting
![]() $R_{1}(t)$
and
$R_{1}(t)$
and
![]() $R_{2}(t).$
We assume that for
$R_{2}(t).$
We assume that for
![]() $i=1,2,$
the random variables
$i=1,2,$
the random variables
![]() $R_{i}(1), R_{i}(2), \ldots, R_{i}\left ( n\right )$
are independent of each other. The probability of stock 1 moving up and down from
$R_{i}(1), R_{i}(2), \ldots, R_{i}\left ( n\right )$
are independent of each other. The probability of stock 1 moving up and down from
![]() $t-1$
to
$t-1$
to
![]() $t$
is denoted by
$t$
is denoted by
![]() $p_{u \cdot }(t)$
and
$p_{u \cdot }(t)$
and
![]() $p_{d \cdot }(t)$
, respectively. For stock 2, these probabilities are denoted by
$p_{d \cdot }(t)$
, respectively. For stock 2, these probabilities are denoted by
![]() $p_{\cdot u}(t)$
and
$p_{\cdot u}(t)$
and
![]() $p_{\cdot d}(t)$
.
$p_{\cdot d}(t)$
.
Assume the financial market is arbitrage free, hence, there exists at least one probability measure
![]() $\mathbb{Q},$
called a risk-neutral probability measure, satisfying the following conditions:
$\mathbb{Q},$
called a risk-neutral probability measure, satisfying the following conditions:
-
1.
 $\mathbb{Q}$
and
$\mathbb{Q}$
and
 $\mathbb{P}$
are equivalent probability measures;
$\mathbb{P}$
are equivalent probability measures; -
2. For any traded asset, its future payoff discounted at the risk-free rate
 $r$
is a martingale with respect to
$r$
is a martingale with respect to
 $\mathbb{Q}$
:(4)
$\mathbb{Q}$
:(4) \begin{equation} \text{e}^{-r}\mathbb{E}_{\mathbb{Q}}\left [ S_{i}(t) |\mathcal{F}_{t-1}\right ] =S_{i}\left ( t-1\right ), \text{ for }i=1,2,\text{and }t=1,2,..,n. \end{equation}
\begin{equation} \text{e}^{-r}\mathbb{E}_{\mathbb{Q}}\left [ S_{i}(t) |\mathcal{F}_{t-1}\right ] =S_{i}\left ( t-1\right ), \text{ for }i=1,2,\text{and }t=1,2,..,n. \end{equation}
If
![]() $\mathbb{Q}$
is a probability measure satisfying the above-stated conditions, we say that it is a feasible risk-neutral probability measure. Under
$\mathbb{Q}$
is a probability measure satisfying the above-stated conditions, we say that it is a feasible risk-neutral probability measure. Under
![]() $\mathbb{Q}$
, the joint probabilities of the random vector
$\mathbb{Q}$
, the joint probabilities of the random vector
![]() $(R_1(t), R_2(t))$
are denoted by
$(R_1(t), R_2(t))$
are denoted by
![]() $q_{u u}(t)$
,
$q_{u u}(t)$
,
![]() $q_{u d}(t)$
,
$q_{u d}(t)$
,
![]() $q_{d u}(t)$
, and
$q_{d u}(t)$
, and
![]() $q_{d d}(t)$
. Additionally, the risk-neutral marginal probabilities in
$q_{d d}(t)$
. Additionally, the risk-neutral marginal probabilities in
![]() $\left [t-1,t\right ]$
are denoted by
$\left [t-1,t\right ]$
are denoted by
![]() $q_{u \cdot }\left (t \right ),q_{d \cdot }\left (t \right ),q_{\cdot u}\left (t \right )$
, and
$q_{u \cdot }\left (t \right ),q_{d \cdot }\left (t \right ),q_{\cdot u}\left (t \right )$
, and
![]() $q_{\cdot d}\left (t \right ).$
We show in the next subsection that this simple market model is incomplete by characterizing the set of feasible risk-neutral probability measures.
$q_{\cdot d}\left (t \right ).$
We show in the next subsection that this simple market model is incomplete by characterizing the set of feasible risk-neutral probability measures.
2.2 The set of equivalent martingale measures
Let us now characterize the set of all feasible risk-neutral probability measures. This set is denoted by
![]() $\mathcal{M}$
. Each
$\mathcal{M}$
. Each
![]() $\mathbb{Q\in }$
$\mathbb{Q\in }$
![]() $\mathcal{M}$
is characterized by the joint probabilities
$\mathcal{M}$
is characterized by the joint probabilities
![]() $ q_{d d}(t)$
,
$ q_{d d}(t)$
,
![]() $q_{u d}(t),$
$q_{u d}(t),$
![]() $q_{d u}(t),$
$q_{d u}(t),$
![]() $q_{u u}(t), t=1,2,\ldots, n$
. In Theorem1, we characterize the risk-neutral pricing measure
$q_{u u}(t), t=1,2,\ldots, n$
. In Theorem1, we characterize the risk-neutral pricing measure
![]() $\mathbb{Q}$
by the correlation coefficients
$\mathbb{Q}$
by the correlation coefficients
![]() $\rho _{\mathbb{Q}}(t)= \text{Corr}_{\mathbb{Q}}\left [ R_{1}(t), R_{2}(t) \right ]$
,
$\rho _{\mathbb{Q}}(t)= \text{Corr}_{\mathbb{Q}}\left [ R_{1}(t), R_{2}(t) \right ]$
,
![]() $t=1,2,\dots, n$
. A proof of this Theorem can be found in Appendix A.1.
$t=1,2,\dots, n$
. A proof of this Theorem can be found in Appendix A.1.
Theorem 1.
Consider the stock price model (
3
) satisfying the conditions (
2
). The set
![]() $\mathcal{M}$
of risk-neutral probability measures can be characterized as follows:
$\mathcal{M}$
of risk-neutral probability measures can be characterized as follows:
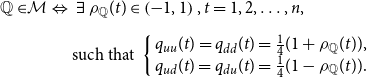 \begin{align} \mathbb{Q\in }\mathcal{M\Leftrightarrow }\text{ } & \text{ }\exists \text{ }\rho _{\mathbb{Q}}(t)\in \left ( -1,1\right ), t=1,2,\ldots, n,\nonumber \\[5pt] & \text{such that }\left \{ \begin{array} [l]{l}q_{u u}(t)=q_{d d}(t) =\frac{1}{4}(1+\rho _{\mathbb{Q}}(t)),\\ q_{u d}(t)=q_{d u}(t) =\frac{1}{4}(1-\rho _{\mathbb{Q}}(t)). \end{array} \right . \end{align}
\begin{align} \mathbb{Q\in }\mathcal{M\Leftrightarrow }\text{ } & \text{ }\exists \text{ }\rho _{\mathbb{Q}}(t)\in \left ( -1,1\right ), t=1,2,\ldots, n,\nonumber \\[5pt] & \text{such that }\left \{ \begin{array} [l]{l}q_{u u}(t)=q_{d d}(t) =\frac{1}{4}(1+\rho _{\mathbb{Q}}(t)),\\ q_{u d}(t)=q_{d u}(t) =\frac{1}{4}(1-\rho _{\mathbb{Q}}(t)). \end{array} \right . \end{align}
The risk-neutral measure
![]() $\mathbb{Q}$
is not unique and the market is incomplete. It is clear to see from Theorem1 that the risk-neutral marginal probabilities are all equal to
$\mathbb{Q}$
is not unique and the market is incomplete. It is clear to see from Theorem1 that the risk-neutral marginal probabilities are all equal to
![]() $\frac{1}{2}$
. Note, however, that our model can be generalized to situations where the marginal risk neutral probabilities are different from
$\frac{1}{2}$
. Note, however, that our model can be generalized to situations where the marginal risk neutral probabilities are different from
![]() $\frac{1}{2}$
. Specifying a feasible risk-neutral measure
$\frac{1}{2}$
. Specifying a feasible risk-neutral measure
![]() $\mathbb{Q}$
under the stock price model (3), requires specifying the correlation efficient
$\mathbb{Q}$
under the stock price model (3), requires specifying the correlation efficient
![]() $\rho _{\mathbb{Q}}(t),t=1,2,\ldots, n.$
Each risk-neutral probability measure
$\rho _{\mathbb{Q}}(t),t=1,2,\ldots, n.$
Each risk-neutral probability measure
![]() $\mathbb{Q}$
in
$\mathbb{Q}$
in
![]() $\mathcal{M}$
has the same marginal distributions but different dependence structures. For instance, take
$\mathcal{M}$
has the same marginal distributions but different dependence structures. For instance, take
![]() $\rho _{\mathbb{Q}}(t)\equiv 0$
, then we find the risk-neutral measure
$\rho _{\mathbb{Q}}(t)\equiv 0$
, then we find the risk-neutral measure
![]() $\mathbb{Q}^{\perp }\in \mathcal{M}$
where the marginals are independent.
$\mathbb{Q}^{\perp }\in \mathcal{M}$
where the marginals are independent.
The situations characterized by the minimal correlation coefficient
![]() $\rho _{\mathbb{Q}^{\min }}(t)\equiv -1$
and the maximal correlation coefficient
$\rho _{\mathbb{Q}^{\min }}(t)\equiv -1$
and the maximal correlation coefficient
![]() $\rho _{\mathbb{Q}^{\max }}(t)\equiv 1$
correspond with the probability measure
$\rho _{\mathbb{Q}^{\max }}(t)\equiv 1$
correspond with the probability measure
![]() $\mathbb{Q}^{\min }$
and the probability measure
$\mathbb{Q}^{\min }$
and the probability measure
![]() $\mathbb{Q}^{\max },$
respectively. The random vector
$\mathbb{Q}^{\max },$
respectively. The random vector
![]() $\left (R_1(t), R_2(t)\right )$
under the probability measure
$\left (R_1(t), R_2(t)\right )$
under the probability measure
![]() $\mathbb{Q}^{\min }$
is counter-monotonic. In this situation, the components of the random vectors are maximum negative dependent. Inversely, the random vector
$\mathbb{Q}^{\min }$
is counter-monotonic. In this situation, the components of the random vectors are maximum negative dependent. Inversely, the random vector
![]() $\left (R_1(t), R_2(t)\right )$
under the probability measure
$\left (R_1(t), R_2(t)\right )$
under the probability measure
![]() $\mathbb{Q}^{\max }$
is comonotonic and the components of the random vector are maximum positive dependent.
$\mathbb{Q}^{\max }$
is comonotonic and the components of the random vector are maximum positive dependent.
The real-world joint probabilities are assumed to be strictly positive, hence all the risk-neutral probabilities specified by (5) are strictly positive. Using (5), we can directly find that for each
![]() $\mathbb{Q} \in \mathcal{M},$
$\mathbb{Q} \in \mathcal{M},$
![]() $\rho _{\mathbb{Q}}(t)\in \left ( -1,1\right )$
, which means that the comonotonic and the counter-monotonic cases are not reachable in
$\rho _{\mathbb{Q}}(t)\in \left ( -1,1\right )$
, which means that the comonotonic and the counter-monotonic cases are not reachable in
![]() $\mathcal{M}$
. The larger
$\mathcal{M}$
. The larger
![]() $\rho _{\mathbb{Q}}(t)$
, the “closer” the risk-neutral probability measure
$\rho _{\mathbb{Q}}(t)$
, the “closer” the risk-neutral probability measure
![]() $\mathbb{Q}$
is to the maximum measure
$\mathbb{Q}$
is to the maximum measure
![]() $\mathbb{Q}^{\max }$
.
$\mathbb{Q}^{\max }$
.
The set
![]() $\mathcal{M}$
contains a wide range of dependence structures. Each element
$\mathcal{M}$
contains a wide range of dependence structures. Each element
![]() $\mathbb{Q}$
in the set
$\mathbb{Q}$
in the set
![]() $\mathcal{M}$
of risk-neutral probability measures can be expressed as a linear combination of
$\mathcal{M}$
of risk-neutral probability measures can be expressed as a linear combination of
![]() $\mathbb{Q}^{\min }$
and
$\mathbb{Q}^{\min }$
and
![]() $\mathbb{Q}^{\max }$
:
$\mathbb{Q}^{\max }$
:
By increasing the correlation coefficient
![]() $\rho _{\mathbb{Q}}(t),$
we can gradually increase the dependence of the components
$\rho _{\mathbb{Q}}(t),$
we can gradually increase the dependence of the components
![]() $R_{1}(t)$
and
$R_{1}(t)$
and
![]() $R_{2}\left (t\right ).$
$R_{2}\left (t\right ).$
It directly follows from (5) that the joint risk-neutral cdf
![]() $F_t^{\mathbb{Q}}$
of the forward return vector
$F_t^{\mathbb{Q}}$
of the forward return vector
![]() $(R_1(t),R_2(t))$
can be given by:
$(R_1(t),R_2(t))$
can be given by:
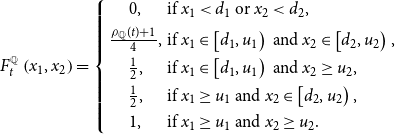 \begin{equation} F_{t}^{_{\mathbb{Q}}}\left ( x_{1},x_{2}\right ) =\left \{ \begin{array}[c]{cl} 0, & \text{if }x_{1}\lt d_1\text{ or }x_{2}\lt d_2,\\[4pt] \frac{\rho _{\mathbb{Q}}(t)+1}{4}, & \text{if }x_{1}\in \left [ d_1,u_1\right ) \text{ and }x_{2}\in \left [d_2,u_2\right ), \\[4pt] \frac{1}{2}, & \text{if }x_{1}\in \left [ d_1,u_1\right ) \text{ and }x_{2}\geq u_2,\\[4pt] \frac{1}{2}, & \text{if }x_{1}\geq u_1\text{ and }x_{2}\in \left [ d_2,u_2\right ), \\[4pt] 1, & \text{if }x_{1}\geq u_1\text{ and }x_{2}\geq u_2.\end{array} \right . \end{equation}
\begin{equation} F_{t}^{_{\mathbb{Q}}}\left ( x_{1},x_{2}\right ) =\left \{ \begin{array}[c]{cl} 0, & \text{if }x_{1}\lt d_1\text{ or }x_{2}\lt d_2,\\[4pt] \frac{\rho _{\mathbb{Q}}(t)+1}{4}, & \text{if }x_{1}\in \left [ d_1,u_1\right ) \text{ and }x_{2}\in \left [d_2,u_2\right ), \\[4pt] \frac{1}{2}, & \text{if }x_{1}\in \left [ d_1,u_1\right ) \text{ and }x_{2}\geq u_2,\\[4pt] \frac{1}{2}, & \text{if }x_{1}\geq u_1\text{ and }x_{2}\in \left [ d_2,u_2\right ), \\[4pt] 1, & \text{if }x_{1}\geq u_1\text{ and }x_{2}\geq u_2.\end{array} \right . \end{equation}
It follows from (7) that the joint risk-neutral cdf of forward return
![]() $F_t^{\mathbb{Q}}(x_1, x_2)$
can be unambiguously determined by the correlation coefficient
$F_t^{\mathbb{Q}}(x_1, x_2)$
can be unambiguously determined by the correlation coefficient
![]() $\rho _{\mathbb{Q}}(t)$
.
$\rho _{\mathbb{Q}}(t)$
.
2.3 Comparing different risk-neutral measures
The set
![]() $\mathcal{M}$
contains different risk-neutral measures such that the marginals
$\mathcal{M}$
contains different risk-neutral measures such that the marginals
![]() $R_1$
and
$R_1$
and
![]() $R_2$
are always the same. Therefore, the difference between multivariate risk-neutral measures is in dependence structure. To compare different probability measures in
$R_2$
are always the same. Therefore, the difference between multivariate risk-neutral measures is in dependence structure. To compare different probability measures in
![]() $\mathcal{M}$
and identify under which one the dependence is stronger or weaker, we can use multivariate stochastic orders. The notion of multivariate stochastic orders in actuarial science goes back to Yanagimoto & Okamoto (Reference Yanagimoto and Okamoto1969).
$\mathcal{M}$
and identify under which one the dependence is stronger or weaker, we can use multivariate stochastic orders. The notion of multivariate stochastic orders in actuarial science goes back to Yanagimoto & Okamoto (Reference Yanagimoto and Okamoto1969).
We first introduce the Positive Quadrant Dependence and the Negative Quadrant Dependence. The notions of PQD and NQD were introduced in Lehmann (Reference Lehmann1966).
Definition 2 (Quadrant Dependence). The random vector
![]() $\left ( R_{1}(t),R_{2}(t)\right )$
is said to be Positive Quadrant Dependent under the probability measure
$\left ( R_{1}(t),R_{2}(t)\right )$
is said to be Positive Quadrant Dependent under the probability measure
![]() $\mathbb{Q},$
notation
$\mathbb{Q},$
notation
![]() $(R_1(t), R_2(t))\sim \mathbb{Q}$
-PQD, in case the vector
$(R_1(t), R_2(t))\sim \mathbb{Q}$
-PQD, in case the vector
![]() $\left ( R_{1}(t),R_{2}(t)\right )$
satisfies:
$\left ( R_{1}(t),R_{2}(t)\right )$
satisfies:
The vector
![]() $\left ( R_{1}(t),R_{2}(t)\right )$
is said to be Negative Quadrant Dependent under the probability measure
$\left ( R_{1}(t),R_{2}(t)\right )$
is said to be Negative Quadrant Dependent under the probability measure
![]() $\mathbb{Q},$
notation
$\mathbb{Q},$
notation
![]() $\mathbb{Q}$
-NQD, in case the vector satisfies:
$\mathbb{Q}$
-NQD, in case the vector satisfies:
where
![]() $F_{t}^{_{\mathbb{Q}}}$
is the joint cdf of
$F_{t}^{_{\mathbb{Q}}}$
is the joint cdf of
![]() $\left ( R_{1}(t),R_{2}(t)\right )$
under the probability measure
$\left ( R_{1}(t),R_{2}(t)\right )$
under the probability measure
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Using Expression (7) for
![]() $F_{t}^{_{\mathbb{Q}}}$
results in the following implications:
$F_{t}^{_{\mathbb{Q}}}$
results in the following implications:
where
![]() $\rho _{\mathbb{Q}^{\perp }}(t)$
is the correlation of the independent copy of the random vector
$\rho _{\mathbb{Q}^{\perp }}(t)$
is the correlation of the independent copy of the random vector
![]() $\left ( R_{1}(t),R_{2}(t) \right )$
, it is straightforward to show that
$\left ( R_{1}(t),R_{2}(t) \right )$
, it is straightforward to show that
![]() $\rho _{\mathbb{Q}^{\perp }}(t)$
equals
$\rho _{\mathbb{Q}^{\perp }}(t)$
equals
![]() $0$
. Using the notion of quadrant dependence, we can measure the joint behavior of two random variables. If the risk-neutral correlation
$0$
. Using the notion of quadrant dependence, we can measure the joint behavior of two random variables. If the risk-neutral correlation
![]() $\rho _{\mathbb{Q}}(t)$
is larger than
$\rho _{\mathbb{Q}}(t)$
is larger than
![]() $0$
, then the random vector
$0$
, then the random vector
![]() $\left (R_{1}(t),R_{2}(t)\right )$
is
$\left (R_{1}(t),R_{2}(t)\right )$
is
![]() $\mathbb{Q}\text{-PQD,}$
which means that the two random variables
$\mathbb{Q}\text{-PQD,}$
which means that the two random variables
![]() $R_{1}(t)$
and
$R_{1}(t)$
and
![]() $R_{2}(t)$
are likely to assume small or large values simultaneously. Conversely, if
$R_{2}(t)$
are likely to assume small or large values simultaneously. Conversely, if
![]() $\rho _{\mathbb{Q}}(t)$
is less than
$\rho _{\mathbb{Q}}(t)$
is less than
![]() $0$
, the random vector is
$0$
, the random vector is
![]() $\mathbb{Q}\text{-NQD,}$
implying an inverse relationship where
$\mathbb{Q}\text{-NQD,}$
implying an inverse relationship where
![]() $R_{1}(t)$
and
$R_{1}(t)$
and
![]() $R_{2}(t)$
may move in different directions.
$R_{2}(t)$
may move in different directions.
The concept of quadrant dependence measures the association between two random variables. However, under different risk-neutral measures
![]() $\mathbb{Q}^{(1)}$
and
$\mathbb{Q}^{(1)}$
and
![]() $\mathbb{Q}^{(2)}$
, the marginals and quadrant dependence of the random vector
$\mathbb{Q}^{(2)}$
, the marginals and quadrant dependence of the random vector
![]() $(R_1(t), R_2(t))$
may be identical. To distinguish the difference under such two different risk-neutral measures, we can use the correlation order introduced in Dhaene & Goovaerts (Reference Dhaene and Goovaerts1996), since the joint distribution of
$(R_1(t), R_2(t))$
may be identical. To distinguish the difference under such two different risk-neutral measures, we can use the correlation order introduced in Dhaene & Goovaerts (Reference Dhaene and Goovaerts1996), since the joint distribution of
![]() $(R_1(t), R_2(t))$
is different when using two different risk-neutral measures.
$(R_1(t), R_2(t))$
is different when using two different risk-neutral measures.
Definition 3 (Correlation order). Consider the risk-neutral probability measures
![]() $\mathbb{Q}^{(1) }$
and
$\mathbb{Q}^{(1) }$
and
![]() $\mathbb{Q}^{(2) }$
with correlation parameters
$\mathbb{Q}^{(2) }$
with correlation parameters
![]() $\rho _{\mathbb{Q}^{(1) }}(t)$
and
$\rho _{\mathbb{Q}^{(1) }}(t)$
and
![]() $\rho _{\mathbb{Q}^{(2) }}(t)$
, respectively. We say that the cdf’s
$\rho _{\mathbb{Q}^{(2) }}(t)$
, respectively. We say that the cdf’s
![]() $F_{t}^{_{\mathbb{Q}^{(1) }}}$
and
$F_{t}^{_{\mathbb{Q}^{(1) }}}$
and
![]() $F_{t}^{_{\mathbb{Q}^{(2) }}}$
are ordered in the correlation order, notation
$F_{t}^{_{\mathbb{Q}^{(2) }}}$
are ordered in the correlation order, notation
![]() $F_{t}^{_{\mathbb{Q}^{(1) }}}\preceq _{\text{Corr}}F_{t}^{_{\mathbb{Q}^{(2) }}}$
if the following holds:
$F_{t}^{_{\mathbb{Q}^{(1) }}}\preceq _{\text{Corr}}F_{t}^{_{\mathbb{Q}^{(2) }}}$
if the following holds:
Intuitively, the inequality
![]() $F_{t}^{_{\mathbb{Q}^{(1) }}}\preceq _{\text{Corr}}F_{t}^{_{\mathbb{Q}^{(2) }}}$
implies that the two stock prices in
$F_{t}^{_{\mathbb{Q}^{(1) }}}\preceq _{\text{Corr}}F_{t}^{_{\mathbb{Q}^{(2) }}}$
implies that the two stock prices in
![]() $[t-1,t]$
move stronger together under the probability measure
$[t-1,t]$
move stronger together under the probability measure
![]() $\mathbb{Q}^{(2) }$
than under the probability measure
$\mathbb{Q}^{(2) }$
than under the probability measure
![]() $\mathbb{Q}^{(1) }$
, i.e., the probability of having simultaneously large/small realizations in
$\mathbb{Q}^{(1) }$
, i.e., the probability of having simultaneously large/small realizations in
![]() $[t-1,t]$
is larger under
$[t-1,t]$
is larger under
![]() $\mathbb{Q}^{\left ( 2\right ) }$
, compared to
$\mathbb{Q}^{\left ( 2\right ) }$
, compared to
![]() $\mathbb{Q}^{(1) }$
. Moreover, comparing the correlations
$\mathbb{Q}^{(1) }$
. Moreover, comparing the correlations
![]() $\rho _{{\mathbb{Q}^{(1) }}}(t)$
and
$\rho _{{\mathbb{Q}^{(1) }}}(t)$
and
![]() $\rho _{{\mathbb{Q}^{(2)}}} (t)$
gives information about the correlation order between the probability measures
$\rho _{{\mathbb{Q}^{(2)}}} (t)$
gives information about the correlation order between the probability measures
![]() $\mathbb{Q}^{(1) }$
and
$\mathbb{Q}^{(1) }$
and
![]() $\mathbb{Q}^{(2) }.$
Indeed, it follows directly from Expression (7) that the following equivalence relation holds:
$\mathbb{Q}^{(2) }.$
Indeed, it follows directly from Expression (7) that the following equivalence relation holds:
There are infinitely many risk-neutral probability measures and each risk-neutral measure models the stock prices using a different dependence structure. If a contingent claim has to be priced, the market will pick a suitable pricing measure.
3. Real world vs risk-neutral measures
Section 2 shows that the market is incomplete and a whole set of risk-neutral measures exists. Market prices are determined by supply and demand, and we assume they do not allow for arbitrage. We also assume that sufficiently many derivatives are traded and these prices are publicly available. All market participants can observe these prices. Having these prices at our disposal allows to back out the choice of the market concerning the risk-neutral measure.
If we can obtain the risk-neutral pricing measure used to price traded derivatives, we can back out the view of the market about future dependencies between the stock prices. However, the market can choose from a wide range of possibilities for
![]() $\rho _{\mathbb{Q}}(t)$
and our results show that there is, mathematically, no reason why the market should take
$\rho _{\mathbb{Q}}(t)$
and our results show that there is, mathematically, no reason why the market should take
![]() $\mathbb{Q}$
such that
$\mathbb{Q}$
such that
![]() $\rho _{\mathbb{Q}}(t)$
is close to the real-world correlation
$\rho _{\mathbb{Q}}(t)$
is close to the real-world correlation
![]() $\rho _{\mathbb{P}}(t)$
for all
$\rho _{\mathbb{P}}(t)$
for all
![]() $t$
.
$t$
.
3.1 A market with a combined asset
From Theorem1, the spot price of stock
![]() $i$
and its potential outcomes
$i$
and its potential outcomes
![]() $d_{i}$
and
$d_{i}$
and
![]() $u_{i}$
, fully specify the distribution of
$u_{i}$
, fully specify the distribution of
![]() $R_i$
. However, individual derivatives written on each stock do not give additional information about the joint distributions. To determine the multivariate distribution, a combined asset and derivative prices on this combined asset are necessary.
$R_i$
. However, individual derivatives written on each stock do not give additional information about the joint distributions. To determine the multivariate distribution, a combined asset and derivative prices on this combined asset are necessary.
Consider the market described above, but now also assume that a stock market index is traded. Its price at time
![]() $0$
is denoted by
$0$
is denoted by
![]() $S(0)$
and its price at time
$S(0)$
and its price at time
![]() $t$
is denoted by
$t$
is denoted by
![]() $S(t)$
:
$S(t)$
:
We have that
![]() $\mathbb{E}_{\mathbb{Q}}\left [ S(t)\right ] =\mathbb{E}_{\mathbb{Q}}\left [ S_{1}(t)+S_{2}(t)\right ] =$
e
$\mathbb{E}_{\mathbb{Q}}\left [ S(t)\right ] =\mathbb{E}_{\mathbb{Q}}\left [ S_{1}(t)+S_{2}(t)\right ] =$
e
![]() $^{rt}S\left ( 0\right ).$
The forward return of the stock market index at time
$^{rt}S\left ( 0\right ).$
The forward return of the stock market index at time
![]() $t$
is denoted by
$t$
is denoted by
![]() $R(t)$
and defined as follows:
$R(t)$
and defined as follows:
Call options on the index with maturity
![]() $T=1,2,\ldots, n$
are also traded. The payoff of an index call option is given by
$T=1,2,\ldots, n$
are also traded. The payoff of an index call option is given by
![]() $\left ( S\left ( T\right ) -K\right ) _{+}\,$
where
$\left ( S\left ( T\right ) -K\right ) _{+}\,$
where
![]() $\left (x\right ) _{+}=\max \left \{x,0\right \}$
. The price of an index call with maturity
$\left (x\right ) _{+}=\max \left \{x,0\right \}$
. The price of an index call with maturity
![]() $T$
and strike
$T$
and strike
![]() $K$
is then denoted by
$K$
is then denoted by
![]() $C_{\mathbb{Q}}\left [ K,T\right ]$
and can be expressed as follows:
$C_{\mathbb{Q}}\left [ K,T\right ]$
and can be expressed as follows:
The cumulative distribution function of the random variable
![]() $S\left ( T\right )$
under the risk-neutral measure
$S\left ( T\right )$
under the risk-neutral measure
![]() $\mathbb{Q}$
is denoted by
$\mathbb{Q}$
is denoted by
![]() $F_{S\left ( T\right ) }^{\mathbb{Q}}$
. We introduce the stop-loss order between two risk-neutral probability measures in terms of their call option curves.
$F_{S\left ( T\right ) }^{\mathbb{Q}}$
. We introduce the stop-loss order between two risk-neutral probability measures in terms of their call option curves.
Definition 4 (Stop-loss order). Consider the stock price model described in (
3
) satisfying the conditions (
2
) and the stock market index defined in (
11
). Consider the risk-neutral probability measures
![]() $\mathbb{Q}^{(1) }$
and
$\mathbb{Q}^{(1) }$
and
![]() $\mathbb{Q}^{(2) }$
. We say that
$\mathbb{Q}^{(2) }$
. We say that
![]() $F_{S\left ( T\right ) }^{\mathbb{Q}^{(1) }}$
and
$F_{S\left ( T\right ) }^{\mathbb{Q}^{(1) }}$
and
![]() $F_{S\left ( T\right ) }^{\mathbb{Q}^{(2) }}$
are ordered in the stop-loss order, notation
$F_{S\left ( T\right ) }^{\mathbb{Q}^{(2) }}$
are ordered in the stop-loss order, notation
![]() $F_{S\left ( T\right ) }^{\mathbb{Q}^{\left ( 1\right ) }}\preceq _{\text{sl}}F_{S\left ( T\right ) }^{\mathbb{Q}^{\left ( 2\right ) }}$
if:
$F_{S\left ( T\right ) }^{\mathbb{Q}^{\left ( 1\right ) }}\preceq _{\text{sl}}F_{S\left ( T\right ) }^{\mathbb{Q}^{\left ( 2\right ) }}$
if:
Intuitively, the stop-loss order relation
![]() $F_{S\left ( T\right )}^{\mathbb{Q}^{\left ( 1\right ) }}\preceq _{\text{sl}}F_{S\left ( T\right ) }^{\mathbb{Q}^{\left ( 2\right ) }}$
implies that the stock market index
$F_{S\left ( T\right )}^{\mathbb{Q}^{\left ( 1\right ) }}\preceq _{\text{sl}}F_{S\left ( T\right ) }^{\mathbb{Q}^{\left ( 2\right ) }}$
implies that the stock market index
![]() $S\left ( T\right )$
is more volatile under the pricing measure
$S\left ( T\right )$
is more volatile under the pricing measure
![]() $\mathbb{Q}^{(2) }$
than under the pricing measure
$\mathbb{Q}^{(2) }$
than under the pricing measure
![]() $\mathbb{Q}^{(1) }.$
Indeed, one can prove the following implication:
$\mathbb{Q}^{(1) }.$
Indeed, one can prove the following implication:
Therefore, call options are more expensive under the measure
![]() $\mathbb{Q}^{\left ( 2\right ) }$
than under
$\mathbb{Q}^{\left ( 2\right ) }$
than under
![]() $\mathbb{Q}^{\left ( 1\right ) }.$
The following theorem shows that the correlation
$\mathbb{Q}^{\left ( 1\right ) }.$
The following theorem shows that the correlation
![]() $\rho _{\mathbb{Q}}\left ( 1\right )$
determines the variability of the stock market index
$\rho _{\mathbb{Q}}\left ( 1\right )$
determines the variability of the stock market index
![]() $S\left ( 1\right ) .$
$S\left ( 1\right ) .$
Theorem 5. Consider the stock price model described in ( 3 ) satisfying the conditions ( 2 ) and the stock market index defined in ( 11 ). Then, the following equivalence relation holds:
Proof.
From (10), we find that
![]() $\rho _{_{\mathbb{Q}^{(1) }}}(1)\leq \rho _{_{\mathbb{Q}^{(2) }}}(1)\iff F_1^{\mathbb{Q}^{(1)}} \preceq _{\text{Corr}} F_1^{\mathbb{Q}^{(2)}}$
. The call option price
$\rho _{_{\mathbb{Q}^{(1) }}}(1)\leq \rho _{_{\mathbb{Q}^{(2) }}}(1)\iff F_1^{\mathbb{Q}^{(1)}} \preceq _{\text{Corr}} F_1^{\mathbb{Q}^{(2)}}$
. The call option price
![]() $C_{\mathbb{Q}}\left [ K,1\right ]$
can be expressed as follows:
$C_{\mathbb{Q}}\left [ K,1\right ]$
can be expressed as follows:
where,
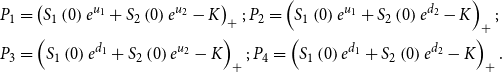 \begin{align*} P_{1} & =\left ( S_{1}\left ( 0\right ) e^{u_{1}}+S_{2}\left ( 0\right ) e^{u_{2}}-K\right ) _{+};\, P_{2}=\left ( S_{1}\left ( 0\right ) e^{u_{1}}+S_{2}\left ( 0\right ) e^{d_{2}}-K\right ) _{+};\\ P_{3} & =\left ( S_{1}\left ( 0\right ) e^{d_{1}}+S_{2}\left ( 0\right ) e^{u_{2}}-K\right ) _{+};\, P_{4}=\left ( S_{1}\left ( 0\right ) e^{d_{1}}+S_{2}\left ( 0\right ) e^{d_{2}}-K\right ) _{+}. \end{align*}
\begin{align*} P_{1} & =\left ( S_{1}\left ( 0\right ) e^{u_{1}}+S_{2}\left ( 0\right ) e^{u_{2}}-K\right ) _{+};\, P_{2}=\left ( S_{1}\left ( 0\right ) e^{u_{1}}+S_{2}\left ( 0\right ) e^{d_{2}}-K\right ) _{+};\\ P_{3} & =\left ( S_{1}\left ( 0\right ) e^{d_{1}}+S_{2}\left ( 0\right ) e^{u_{2}}-K\right ) _{+};\, P_{4}=\left ( S_{1}\left ( 0\right ) e^{d_{1}}+S_{2}\left ( 0\right ) e^{d_{2}}-K\right ) _{+}. \end{align*}
It follows from Expression (14) that
![]() $C_{\mathbb{Q}}\left [ K,1\right ]$
is an increasing linear function of
$C_{\mathbb{Q}}\left [ K,1\right ]$
is an increasing linear function of
![]() $\rho _{\mathbb{Q}}(1), $
since
$\rho _{\mathbb{Q}}(1), $
since
![]() $(P_{1}-P_{2}-P_{3}+P_{4})\geq 0.$
$(P_{1}-P_{2}-P_{3}+P_{4})\geq 0.$
The time
![]() $0$
market price of a call option with strike
$0$
market price of a call option with strike
![]() $K$
and maturity
$K$
and maturity
![]() $1$
year, denoted by
$1$
year, denoted by
![]() $C_{\mathbb{Q}}\left [ K,1\right ]$
, can then be used to extract the correlation
$C_{\mathbb{Q}}\left [ K,1\right ]$
, can then be used to extract the correlation
![]() $\rho _{\mathbb{Q}}\left ( 1\right )$
associated with the risk-neutral measure
$\rho _{\mathbb{Q}}\left ( 1\right )$
associated with the risk-neutral measure
![]() $\mathbb{Q}$
, as demonstrated in (14). Indeed, we have that:
$\mathbb{Q}$
, as demonstrated in (14). Indeed, we have that:
From Theorem1, the joint probabilities
![]() $q_{d d}(1), q_{d u}(1), q_{u d}(1), q_{u u}(1)$
in this case are fully specified. For the single period case, Theorem 5 also indicates the equivalence relation between the correlation of two stocks and the volatility of the stock index. Moreover, we provide the following Theorem6 to show that having available the option prices
$q_{d d}(1), q_{d u}(1), q_{u d}(1), q_{u u}(1)$
in this case are fully specified. For the single period case, Theorem 5 also indicates the equivalence relation between the correlation of two stocks and the volatility of the stock index. Moreover, we provide the following Theorem6 to show that having available the option prices
![]() $C_{\mathbb{Q}}\left [ K,T\right ], $
for
$C_{\mathbb{Q}}\left [ K,T\right ], $
for
![]() $T=1,2,\ldots, n,$
one can back out the pricing measure
$T=1,2,\ldots, n,$
one can back out the pricing measure
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Theorem 6.
Assume the index call option prices
![]() $C_{\mathbb{Q}}\left [ K,T\right ], T = 1,2,\ldots, n$
are all available, then the correlation coefficient
$C_{\mathbb{Q}}\left [ K,T\right ], T = 1,2,\ldots, n$
are all available, then the correlation coefficient
![]() $\rho _{\mathbb{Q}}(t), t =1,2,\ldots, n$
can unambiguously be determined.
$\rho _{\mathbb{Q}}(t), t =1,2,\ldots, n$
can unambiguously be determined.
Proof.
First, we already determined
![]() $\rho _{\mathbb{Q}}(1)$
from expression (15). Next, knowledge about the price
$\rho _{\mathbb{Q}}(1)$
from expression (15). Next, knowledge about the price
![]() $C_{\mathbb{Q}}[K,2]$
enables us to back out the correlation
$C_{\mathbb{Q}}[K,2]$
enables us to back out the correlation
![]() $\rho _{\mathbb{Q}}(2)$
. Indeed, we can write:
$\rho _{\mathbb{Q}}(2)$
. Indeed, we can write:
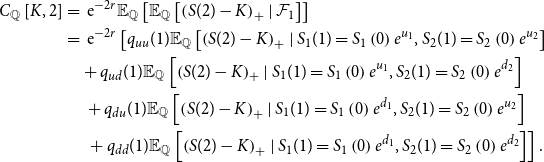 \begin{align} C_{\mathbb{Q}}\left [ K,2\right ] &=\text{ } \text{e}^{-2r}\mathbb{E}_{\mathbb{Q}}\left [ \mathbb{E}_{\mathbb{Q}}\left [ \left ( S(2) -K\right ) _{+}\mid \mathcal{F}_{1}\right ] \right ] \nonumber \\ &=\text{ } \text{e}^{-2r}\left [ q_{u u}(1) \mathbb{E}_{\mathbb{Q}}\left [ \left ( S(2) -K\right ) _{+}\mid S_{1}(1) =S_{1}\left ( 0\right ) e^{u_{1}},S_{2}(1) =S_{2}\left ( 0\right ) e^{u_{2}}\right ] \right . \nonumber \\ \text{ } &\quad +q_{u d}(1) \mathbb{E}_{\mathbb{Q}}\left [ \left ( S(2) -K\right ) _{+}\mid S_{1}(1) =S_{1}\left ( 0\right ) e^{u_{1}},S_{2}(1) =S_{2}\left ( 0\right ) e^{d_{2}}\right ] \nonumber \\ &\quad \text{ }+q_{d u}(1) \mathbb{E}_{\mathbb{Q}}\left [ \left ( S(2) -K\right ) _{+}\mid S_{1}(1) =S_{1}\left ( 0\right ) e^{d_{1}},S_{2}(1) =S_{2}\left ( 0\right ) e^{u_{2}}\right ] \nonumber \\ &\quad \text{ }\left . +\text{ }q_{d d}(1) \mathbb{E}_{\mathbb{Q}}\left [ \left ( S(2) -K\right ) _{+}\mid S_{1}(1) =S_{1}\left ( 0\right ) e^{d_{1}},S_{2}(1) =S_{2}\left ( 0\right ) e^{d_{2}}\right ] \right ] . \end{align}
\begin{align} C_{\mathbb{Q}}\left [ K,2\right ] &=\text{ } \text{e}^{-2r}\mathbb{E}_{\mathbb{Q}}\left [ \mathbb{E}_{\mathbb{Q}}\left [ \left ( S(2) -K\right ) _{+}\mid \mathcal{F}_{1}\right ] \right ] \nonumber \\ &=\text{ } \text{e}^{-2r}\left [ q_{u u}(1) \mathbb{E}_{\mathbb{Q}}\left [ \left ( S(2) -K\right ) _{+}\mid S_{1}(1) =S_{1}\left ( 0\right ) e^{u_{1}},S_{2}(1) =S_{2}\left ( 0\right ) e^{u_{2}}\right ] \right . \nonumber \\ \text{ } &\quad +q_{u d}(1) \mathbb{E}_{\mathbb{Q}}\left [ \left ( S(2) -K\right ) _{+}\mid S_{1}(1) =S_{1}\left ( 0\right ) e^{u_{1}},S_{2}(1) =S_{2}\left ( 0\right ) e^{d_{2}}\right ] \nonumber \\ &\quad \text{ }+q_{d u}(1) \mathbb{E}_{\mathbb{Q}}\left [ \left ( S(2) -K\right ) _{+}\mid S_{1}(1) =S_{1}\left ( 0\right ) e^{d_{1}},S_{2}(1) =S_{2}\left ( 0\right ) e^{u_{2}}\right ] \nonumber \\ &\quad \text{ }\left . +\text{ }q_{d d}(1) \mathbb{E}_{\mathbb{Q}}\left [ \left ( S(2) -K\right ) _{+}\mid S_{1}(1) =S_{1}\left ( 0\right ) e^{d_{1}},S_{2}(1) =S_{2}\left ( 0\right ) e^{d_{2}}\right ] \right ] . \end{align}
From Expression (14), we find that the conditional expectations are given by:
where the constants
![]() $P_{j}$
,
$P_{j}$
,
![]() $j=1,2,3,4,$
are now defined as follows:
$j=1,2,3,4,$
are now defined as follows:
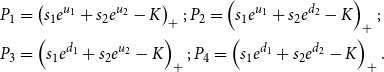 \begin{align*} P_{1} & =\left ( s_{1}e^{u_{1}}+s_{2}e^{u_{2}}-K\right ) _{+};\,P_{2}=\left ( s_{1}e^{u_{1}}+s_{2}e^{d_{2}}-K\right ) _{+};\\ P_{3} & =\left ( s_{1}e^{d_{1}}+s_{2}e^{u_{2}}-K\right ) _{+};\,P_{4}=\left ( s_{1}e^{d_{1}}+s_{2}e^{d_{2}}-K\right ) _{+}. \end{align*}
\begin{align*} P_{1} & =\left ( s_{1}e^{u_{1}}+s_{2}e^{u_{2}}-K\right ) _{+};\,P_{2}=\left ( s_{1}e^{u_{1}}+s_{2}e^{d_{2}}-K\right ) _{+};\\ P_{3} & =\left ( s_{1}e^{d_{1}}+s_{2}e^{u_{2}}-K\right ) _{+};\,P_{4}=\left ( s_{1}e^{d_{1}}+s_{2}e^{d_{2}}-K\right ) _{+}. \end{align*}
The probabilities
![]() $q_{u u}(1), q_{u d}(1), q_{d u}(1), q_{d d}(1)$
are already determined from the call option price
$q_{u u}(1), q_{u d}(1), q_{d u}(1), q_{d d}(1)$
are already determined from the call option price
![]() $C_{\mathbb{Q}}[K,1]$
. As a result, the only unknown parameter in the Expression (16) is
$C_{\mathbb{Q}}[K,1]$
. As a result, the only unknown parameter in the Expression (16) is
![]() $\rho _{\mathbb{Q}}(2)$
and observing the option price
$\rho _{\mathbb{Q}}(2)$
and observing the option price
![]() $C_{\mathbb{Q}}\left [ K,2\right ]$
allows to solve for
$C_{\mathbb{Q}}\left [ K,2\right ]$
allows to solve for
![]() $\rho _{\mathbb{Q}}(2).$
Suppose we have derived the correlations
$\rho _{\mathbb{Q}}(2).$
Suppose we have derived the correlations
![]() $\rho _{\mathbb{Q}}(t), t=1,2,\ldots, i$
, where
$\rho _{\mathbb{Q}}(t), t=1,2,\ldots, i$
, where
![]() $i\lt n$
, we can then apply the same approach to acquire the correlation
$i\lt n$
, we can then apply the same approach to acquire the correlation
![]() $\rho _{\mathbb{Q}}\left ( i+1\right )$
from the correlations
$\rho _{\mathbb{Q}}\left ( i+1\right )$
from the correlations
![]() $\rho _{\mathbb{Q}}(1)$
,
$\rho _{\mathbb{Q}}(1)$
,
![]() $\rho _{\mathbb{Q}}(2)$
,
$\rho _{\mathbb{Q}}(2)$
,
![]() $\dots, \rho _{\mathbb{Q}}\left ( i\right )$
and the index option price
$\dots, \rho _{\mathbb{Q}}\left ( i\right )$
and the index option price
![]() $C_{\mathbb{Q}}\left [ K,i+1\right ]$
. The probability distributions of
$C_{\mathbb{Q}}\left [ K,i+1\right ]$
. The probability distributions of
![]() $S_1(i)$
and
$S_1(i)$
and
![]() $S_2(i)$
can be specified using
$S_2(i)$
can be specified using
![]() $\rho _{\mathbb{Q}}\left ( 1\right )$
,
$\rho _{\mathbb{Q}}\left ( 1\right )$
,
![]() $\rho _{\mathbb{Q}}\left ( 2\right ), \dots, \rho _{\mathbb{Q}}\left ( i\right )$
. Hence, by using the option price
$\rho _{\mathbb{Q}}\left ( 2\right ), \dots, \rho _{\mathbb{Q}}\left ( i\right )$
. Hence, by using the option price
![]() $C_{\mathbb{Q}}\left [ K,i+1\right ]$
, we can solve for
$C_{\mathbb{Q}}\left [ K,i+1\right ]$
, we can solve for
![]() $\rho _{\mathbb{Q}}\left ( i+1\right )$
. Therefore, we conclude that having available the option prices
$\rho _{\mathbb{Q}}\left ( i+1\right )$
. Therefore, we conclude that having available the option prices
![]() $C_{\mathbb{Q}}\left [ K,T\right ], $
for
$C_{\mathbb{Q}}\left [ K,T\right ], $
for
![]() $T=1,2,\ldots, n$
, one can back out the pricing measure
$T=1,2,\ldots, n$
, one can back out the pricing measure
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Theorem6 showed that adding index call options with maturities
![]() $t=1,2,\ldots, T,$
completes the market described in (3). Indeed, one can back out the risk-neutral correlation using index call options, and therefore the risk-neutral probability measure is unique in this market setting. The idea of extracting the implied correlation from available multivariate option prices is widely discussed in the literature. For example, Linders & Schoutens (Reference Linders and Schoutens2014) used basket option prices, Ballotta et al. (Reference Ballotta, Deelstra and Rayée2017) used quanto options, and Garcia et al. (Reference Garcia, Goossens, Masol and Schoutens2009) derived implied correlations using CDO spreads.
$t=1,2,\ldots, T,$
completes the market described in (3). Indeed, one can back out the risk-neutral correlation using index call options, and therefore the risk-neutral probability measure is unique in this market setting. The idea of extracting the implied correlation from available multivariate option prices is widely discussed in the literature. For example, Linders & Schoutens (Reference Linders and Schoutens2014) used basket option prices, Ballotta et al. (Reference Ballotta, Deelstra and Rayée2017) used quanto options, and Garcia et al. (Reference Garcia, Goossens, Masol and Schoutens2009) derived implied correlations using CDO spreads.
Prices of traded stocks and options can be used to back out the corresponding risk-neutral pricing measure, the correlation of the stock returns and the volatility of the stock market index. We refer to these quantities as implied measures, implied correlation, implied volatility. Note that market prices are expectations under the pricing measure
![]() $\mathbb{Q}$
and therefore the implied correlation and the implied volatility have to be understood as correlation and volatility levels with respect to the risk-neutral probability measure
$\mathbb{Q}$
and therefore the implied correlation and the implied volatility have to be understood as correlation and volatility levels with respect to the risk-neutral probability measure
![]() $\mathbb{Q}$
. Correlation and volatility under the probability
$\mathbb{Q}$
. Correlation and volatility under the probability
![]() $\mathbb{P}$
are referred to as real-world correlation and volatility, respectively.
$\mathbb{P}$
are referred to as real-world correlation and volatility, respectively.
3.2 Example: A single period model
We consider a one-period financial market as described in Section 2. The risk-free rate
![]() $r$
is assumed to be
$r$
is assumed to be
![]() $0$
and consider
$0$
and consider
![]() $e^{u_1}=1.4$
,
$e^{u_1}=1.4$
,
![]() $e^{u_2}=1.7$
. The time
$e^{u_2}=1.7$
. The time
![]() $0$
spot prices of the traded assets are given by
$0$
spot prices of the traded assets are given by
![]() $S_{1}\left ( 0\right ) =100$
and
$S_{1}\left ( 0\right ) =100$
and
![]() $S_{2}\left ( 0\right ) =200$
. The dynamics of the financial market under the real-world measure
$S_{2}\left ( 0\right ) =200$
. The dynamics of the financial market under the real-world measure
![]() $\mathbb{P}$
are described by the following equations:
$\mathbb{P}$
are described by the following equations:
Notice that we choose the marginals such that the
![]() $\mathbb{P}$
-marginals are the same as the
$\mathbb{P}$
-marginals are the same as the
![]() $\mathbb{Q}$
-marginals, this is to make the example simpler and is not required in general case.
$\mathbb{Q}$
-marginals, this is to make the example simpler and is not required in general case.
Consider the stock market index
![]() $S(t)=S_{1}(t) +S_{2}(t), $
$S(t)=S_{1}(t) +S_{2}(t), $
![]() $t=0,1.$
We find that the real-world correlation
$t=0,1.$
We find that the real-world correlation
![]() $\rho _{\mathbb{P}}(1) = \text{Corr}[R_1(1), R_2(1)] = 0.2,$
and the real-world volatility
$\rho _{\mathbb{P}}(1) = \text{Corr}[R_1(1), R_2(1)] = 0.2,$
and the real-world volatility
![]() $\sigma _{\mathbb{P}}(1) =\sqrt{\text{Var}_{\mathbb{P}}\left [ R(1) \right ]} = 0.585.$
Since
$\sigma _{\mathbb{P}}(1) =\sqrt{\text{Var}_{\mathbb{P}}\left [ R(1) \right ]} = 0.585.$
Since
![]() $\rho _{\mathbb{P}}(1) =0.2\gt 0$
, the return vector
$\rho _{\mathbb{P}}(1) =0.2\gt 0$
, the return vector
![]() $\left ( R_{1}(1), R_{2}(1) \right )$
is Positive Quadrant Dependent under the real-world probability measure
$\left ( R_{1}(1), R_{2}(1) \right )$
is Positive Quadrant Dependent under the real-world probability measure
![]() $\mathbb{P}$
:
$\mathbb{P}$
:
We conclude from (18) that stocks are positively dependent under the real-world measure
![]() $\mathbb{P}$
specified by (17). However, the dependence structure under the risk-neutral measure
$\mathbb{P}$
specified by (17). However, the dependence structure under the risk-neutral measure
![]() $\mathbb{Q}$
can be different, even opposite from the dependence under
$\mathbb{Q}$
can be different, even opposite from the dependence under
![]() $\mathbb{P}$
. The following Proposition1 is presented to show that the stock prices can be negatively dependent under the risk-neutral measure.
$\mathbb{P}$
. The following Proposition1 is presented to show that the stock prices can be negatively dependent under the risk-neutral measure.
Proposition 1.
A call option written on the stock market index
![]() $S(1)$
, with strike
$S(1)$
, with strike
![]() $K = 300$
, is traded and its time
$K = 300$
, is traded and its time
![]() $0$
price
$0$
price
![]() $\hat{C}_{\mathbb{Q}}$
can be observed in the market. Then we have the following equivalence relations:
$\hat{C}_{\mathbb{Q}}$
can be observed in the market. Then we have the following equivalence relations:
Proof.
From (14), we have
![]() $\hat{C}_{\mathbb{Q}} = 70 + 20\rho _{\mathbb{Q}}(1).$
Hence, it follows from (8) directly to derive (19).
$\hat{C}_{\mathbb{Q}} = 70 + 20\rho _{\mathbb{Q}}(1).$
Hence, it follows from (8) directly to derive (19).
Proposition1 shows that the market decides if the stocks are positive or negative dependent under the risk-neutral measure. Indeed, different market situations result in different risk-neutral measures, which can be different with the real-world measure
![]() $\mathbb{P}$
. Here we provide three different market situations in Table 1.
$\mathbb{P}$
. Here we provide three different market situations in Table 1.
From Table 1, we can also conclude that the risk-neutral pricing measures
![]() $\mathbb{Q}^{(1) }$
,
$\mathbb{Q}^{(1) }$
,
![]() $\mathbb{Q}^{(2) }$
, and
$\mathbb{Q}^{(2) }$
, and
![]() $\mathbb{Q}^{\left ( 3\right ) }$
are ordered in the correlation order:
$\mathbb{Q}^{\left ( 3\right ) }$
are ordered in the correlation order:
This example shows that deriving the implied correlation and volatility to learn about the future dynamics of the stock prices is only part of the story. Implied measures are giving information about the risk-neutral dynamics and these statements cannot be directly translated to statements under the real-world probability measure. If the risk-neutral measure
![]() $\mathbb{Q}^{(1)}$
is chosen by the market, then implied volatility and correlation are substantially different with the real-world volatility and correlation. It might feel counter-intuitive to use a negative dependence structure to price the index option while under the real-world probability measure, the stocks are positive dependent. Notice that, however, the corresponding index option price does not lead to arbitrage and is consistent with other derivative prices.
$\mathbb{Q}^{(1)}$
is chosen by the market, then implied volatility and correlation are substantially different with the real-world volatility and correlation. It might feel counter-intuitive to use a negative dependence structure to price the index option while under the real-world probability measure, the stocks are positive dependent. Notice that, however, the corresponding index option price does not lead to arbitrage and is consistent with other derivative prices.
Table 1. Three different market situations given that
![]() $\rho _{\mathbb{P}} = 0.2$
and
$\rho _{\mathbb{P}} = 0.2$
and
![]() $\sigma _{\mathbb{P}} = 0.585$
$\sigma _{\mathbb{P}} = 0.585$

3.3 Example: A multiperiod model
Consider the financial market described above, but now we consider the future times
![]() $t=1,2,\ldots, 10.$
Assume that the real-world correlation
$t=1,2,\ldots, 10.$
Assume that the real-world correlation
![]() $\rho _{\mathbb{P}}(t)$
is given by
$\rho _{\mathbb{P}}(t)$
is given by
![]() $\rho _{\mathbb{P}}(t) = 0.92 - 0.08t, \text{ for } t=1,2,\ldots 10.$
Similar to the one-period case, we still assume the real-world marginals are the same as the risk-neutral marginals, then the real-world dynamics can be expressed as:
$\rho _{\mathbb{P}}(t) = 0.92 - 0.08t, \text{ for } t=1,2,\ldots 10.$
Similar to the one-period case, we still assume the real-world marginals are the same as the risk-neutral marginals, then the real-world dynamics can be expressed as:
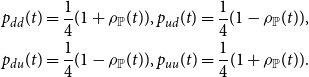 \begin{align} p_{d d}(t) =\frac{1}{4}(1+\rho _{\mathbb{P}}(t))&, p_{u d}(t) =\frac{1}{4}(1-\rho _{\mathbb{P}}(t)), \\ p_{d u}(t) =\frac{1}{4}(1-\rho _{\mathbb{P}}(t))&, \nonumber p_{u u}(t) =\frac{1}{4}(1+\rho _{\mathbb{P}}(t)).\nonumber \end{align}
\begin{align} p_{d d}(t) =\frac{1}{4}(1+\rho _{\mathbb{P}}(t))&, p_{u d}(t) =\frac{1}{4}(1-\rho _{\mathbb{P}}(t)), \\ p_{d u}(t) =\frac{1}{4}(1-\rho _{\mathbb{P}}(t))&, \nonumber p_{u u}(t) =\frac{1}{4}(1+\rho _{\mathbb{P}}(t)).\nonumber \end{align}
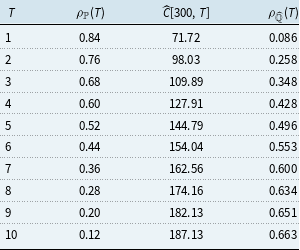
We show real-world correlations in the second column of Table 2.
Table 2. Real-world and risk-neutral correlations
Assume at time 0, at-the-money call options with maturities
![]() $T=1,2,\ldots, 10$
are traded. The market prices are denoted by
$T=1,2,\ldots, 10$
are traded. The market prices are denoted by
![]() $\widehat{C}\left [ 300,T\right ], \text{ where }T=1,2,\ldots, 10,$
and are given in the third column of Table 2. The market prices can be used to determine the unique risk-neutral measure
$\widehat{C}\left [ 300,T\right ], \text{ where }T=1,2,\ldots, 10,$
and are given in the third column of Table 2. The market prices can be used to determine the unique risk-neutral measure
![]() $\widehat{\mathbb{Q}}$
. Indeed, Theorem6 shows that implied correlations
$\widehat{\mathbb{Q}}$
. Indeed, Theorem6 shows that implied correlations
![]() $\rho _{\widehat{\mathbb{Q}}}(t)$
can be uniquely determined by index call option prices
$\rho _{\widehat{\mathbb{Q}}}(t)$
can be uniquely determined by index call option prices
![]() $\widehat{C}[300,t]$
for
$\widehat{C}[300,t]$
for
![]() $t=1,2,\dots, n$
. We present implied correlations
$t=1,2,\dots, n$
. We present implied correlations
![]() $\rho _{\widehat{\mathbb{Q}}}(t)$
in the fourth column of Table 2. We can find from Table 2 that there always exists a gap between real-world and implied correlations. We call this gap the correlation gap. The following Fig. 1 shows the plot of the correlation gap,
$\rho _{\widehat{\mathbb{Q}}}(t)$
in the fourth column of Table 2. We can find from Table 2 that there always exists a gap between real-world and implied correlations. We call this gap the correlation gap. The following Fig. 1 shows the plot of the correlation gap,
![]() $\rho _{\mathbb{P}}(t) - \rho _{\widehat{\mathbb{Q}}}(t)$
for time
$\rho _{\mathbb{P}}(t) - \rho _{\widehat{\mathbb{Q}}}(t)$
for time
![]() $t = 1, 2, \dots, 10.$
$t = 1, 2, \dots, 10.$
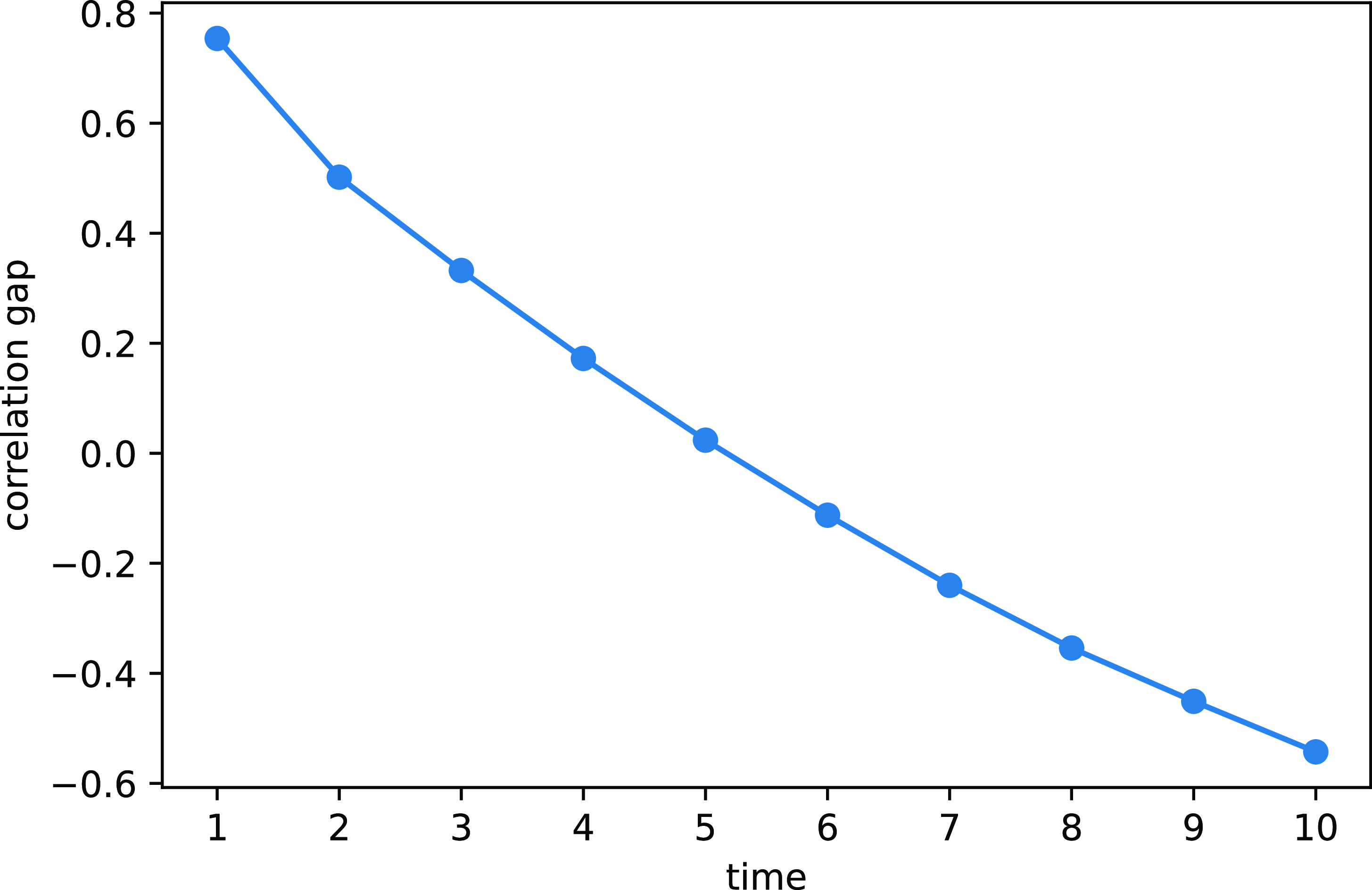
Figure 1 The correlation gap
![]() $\rho _{\mathbb{P}}(t) - \rho _{\widehat{\mathbb{Q}}}(t)$
with respect to time
$\rho _{\mathbb{P}}(t) - \rho _{\widehat{\mathbb{Q}}}(t)$
with respect to time
![]() $t$
.
$t$
.
Implied correlations capture the aggregate view of the market about future risk-neutral correlations. Table 2 and Fig. 1 clearly show that these views cannot always be directly translated to real-world statements. Indeed, in our example, the risk-neutral correlation is increasing: market participants anticipate a increase in correlation. However, the real-world correlation is moving in the opposite direction and decreases over time. Moreover, we can see from Fig. 1 that the correlation gap
![]() $\rho _{\mathbb{P}}(t) - \rho _{\widehat{\mathbb{Q}}}(t)$
is decreasing over time. The correlation gap is highly positive at time
$\rho _{\mathbb{P}}(t) - \rho _{\widehat{\mathbb{Q}}}(t)$
is decreasing over time. The correlation gap is highly positive at time
![]() $1$
and becoming strongly negative at time
$1$
and becoming strongly negative at time
![]() $10$
. Notably, a nonzero correlation gap may persist in the financial market over time. In the next Section 4, we demonstrate that this nonzero correlation gap not only manifests in the financial market but also carries implications for the purchase of unit-linked insurance products.
$10$
. Notably, a nonzero correlation gap may persist in the financial market over time. In the next Section 4, we demonstrate that this nonzero correlation gap not only manifests in the financial market but also carries implications for the purchase of unit-linked insurance products.
4. The correlation gap: Market-consistent valuation for insurance products
Consider an insurer selling a unit-linked product to a group of
![]() $N$
policyholders of the same age
$N$
policyholders of the same age
![]() $x$
. For
$x$
. For
![]() $i = 1,2,\dots, N,$
, we denote by
$i = 1,2,\dots, N,$
, we denote by
![]() $I_i$
the indicator random variable modeling the survival of the policyholder
$I_i$
the indicator random variable modeling the survival of the policyholder
![]() $i$
,
$i$
,
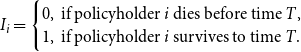 \begin{equation} I_i = \begin{cases} 0, \text{ if policyholder $i$ dies before time }T,\\ 1, \text{ if policyholder $i$ survives to time }T. \end{cases} \end{equation}
\begin{equation} I_i = \begin{cases} 0, \text{ if policyholder $i$ dies before time }T,\\ 1, \text{ if policyholder $i$ survives to time }T. \end{cases} \end{equation}
The payoff of this unit-linked contract depends on the performance of a stock market fund. We assume here, for simplicity, the fund consists of two stocks
![]() $S_1(t)$
and
$S_1(t)$
and
![]() $S_2(t)$
. However, if the fund value drops below a threshold
$S_2(t)$
. However, if the fund value drops below a threshold
![]() $K$
at time
$K$
at time
![]() $T$
, the insurer will compensate such that the policy holder still receives the payoff
$T$
, the insurer will compensate such that the policy holder still receives the payoff
![]() $K$
. To be more specific, policyholder
$K$
. To be more specific, policyholder
![]() $i$
receives upon survival at time
$i$
receives upon survival at time
![]() $T$
the payoff
$T$
the payoff
![]() $h_i(T)$
given by:
$h_i(T)$
given by:
Then the per-policy payout of the insurer is denoted by
![]() $h(T)$
and given by:
$h(T)$
and given by:
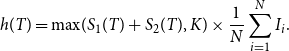 \begin{equation} h(T) = \text{max}(S_1(T)+S_2(T), K)\times \frac{1}{N}\sum _{i=1}^N I_i. \end{equation}
\begin{equation} h(T) = \text{max}(S_1(T)+S_2(T), K)\times \frac{1}{N}\sum _{i=1}^N I_i. \end{equation}
We assume the survival random variables
![]() $I_1, I_2, \ldots, I_n$
are i.i.d. and each
$I_1, I_2, \ldots, I_n$
are i.i.d. and each
![]() $I_i$
is independent from the stock prices
$I_i$
is independent from the stock prices
![]() $S_1(T)$
and
$S_1(T)$
and
![]() $S_2(T)$
. Moreover, we assume that
$S_2(T)$
. Moreover, we assume that
![]() $\mathbb{P}\left [I_i=1\right ] ={}_Tp_x.$
$\mathbb{P}\left [I_i=1\right ] ={}_Tp_x.$
Market-consistent valuations are considered extensively for the valuation of unit-linked insurance products, see, e.g., Malamud et al. (Reference Malamud, Trubowitz and Wüthrich2008), Artzner & Eisele (Reference Artzner and Eisele2010), Pelsser & Stadje (Reference Pelsser and Stadje2014), Dhaene et al. (Reference Dhaene, Stassen, Barigou and Chen2017), and Linders (Reference Linders2023). A market-consistent valuation can be interpreted in the sense that the valuation of any hedgeable part within a claim aligns with the price of its hedge. Now let us consider a market-consistent (MC) valuation for the unit-linked insurance product with payout per policy given by (23). Denote this MC valuation by
![]() $\rho [h(T)]$
and it is given by:
$\rho [h(T)]$
and it is given by:
Assume that
![]() $N$
is large and the insurance risk can be diversified. For simplicity, here, we use the best-estimate for the valuation of the actuarial risk within
$N$
is large and the insurance risk can be diversified. For simplicity, here, we use the best-estimate for the valuation of the actuarial risk within
![]() $h(T)$
. Hence, we can regard the valuation
$h(T)$
. Hence, we can regard the valuation
![]() $\rho (h(T))$
as a MC valuation based on perfect actuarial diversification. By using the fact that
$\rho (h(T))$
as a MC valuation based on perfect actuarial diversification. By using the fact that
![]() $e^{-rT}\mathbb{E}^{\mathbb{Q}}[\text{max}(S_1(T)+S_2(T), K)]$
is equal to
$e^{-rT}\mathbb{E}^{\mathbb{Q}}[\text{max}(S_1(T)+S_2(T), K)]$
is equal to
![]() $C_{\mathbb{Q}}[K,T] + Ke^{-rT}$
, the value
$C_{\mathbb{Q}}[K,T] + Ke^{-rT}$
, the value
![]() $\rho [h(T)]$
can be rewritten as:
$\rho [h(T)]$
can be rewritten as:
In a broader context, market-consistent valuations can fulfill different purposes, which can be employed not only in determining technical provisions but also in setting premiums. Assume that
![]() $\rho [h(T)]$
is the premium charged by the insurance company for each policyholder. The expected payoff for policyholder
$\rho [h(T)]$
is the premium charged by the insurance company for each policyholder. The expected payoff for policyholder
![]() $i$
at time
$i$
at time
![]() $T$
is given by
$T$
is given by
![]() $\mathbb{E}^{\mathbb{P}}[h_i(T)]$
and can be expressed as:
$\mathbb{E}^{\mathbb{P}}[h_i(T)]$
and can be expressed as:
It directly follows (24) and (26) that the time
![]() $T$
expected excess return above the risk-free return (Expected ER) for each policyholder to buy this unit-linked insurance product is given by:
$T$
expected excess return above the risk-free return (Expected ER) for each policyholder to buy this unit-linked insurance product is given by:
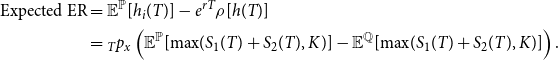 \begin{align} \text{Expected ER} &= \mathbb{E}^{\mathbb{P}}[h_i(T)]-e^{rT}\rho [h(T)] \\ &={_{T}p_x}\left (\mathbb{E}^{\mathbb{P}}[\text{max}(S_1(T)+S_2(T), K)] - \mathbb{E}^{\mathbb{Q}}[\text{max}(S_1(T)+S_2(T), K)]\right ).\nonumber \end{align}
\begin{align} \text{Expected ER} &= \mathbb{E}^{\mathbb{P}}[h_i(T)]-e^{rT}\rho [h(T)] \\ &={_{T}p_x}\left (\mathbb{E}^{\mathbb{P}}[\text{max}(S_1(T)+S_2(T), K)] - \mathbb{E}^{\mathbb{Q}}[\text{max}(S_1(T)+S_2(T), K)]\right ).\nonumber \end{align}
By recognizing that
![]() $\mathbb{E}^{\mathbb{P}}[\text{max}(S_1(T)+S_2(T), K)]$
can also be written as
$\mathbb{E}^{\mathbb{P}}[\text{max}(S_1(T)+S_2(T), K)]$
can also be written as
![]() $K+\mathbb{E}^{\mathbb{P}}[(S_1(T)+S_2(T)-K)_+]$
, the expected excess return for purchasing this unit-linked insurance contract can be rewritten as:
$K+\mathbb{E}^{\mathbb{P}}[(S_1(T)+S_2(T)-K)_+]$
, the expected excess return for purchasing this unit-linked insurance contract can be rewritten as:
From (28), it is evident that the expected excess return for buying this unit-linked insurance contract depends on the expected excess return for investing in the index call option with a strike
![]() $K$
and a maturity
$K$
and a maturity
![]() $T$
. In Section 3.1, it is shown that implied correlations can be uniquely determined from the index call option prices. Hence, the expected excess return for each policyholder is associated with implied correlations. In the following subsection, we examine the same market setting in Example 3.2 to illustrate that the expected excess return for the policyholder of this unit-linked insurance can be determined by the correlation gap in the financial market.
$T$
. In Section 3.1, it is shown that implied correlations can be uniquely determined from the index call option prices. Hence, the expected excess return for each policyholder is associated with implied correlations. In the following subsection, we examine the same market setting in Example 3.2 to illustrate that the expected excess return for the policyholder of this unit-linked insurance can be determined by the correlation gap in the financial market.
4.1 Illustration: A single period model
Example 3.2 illustrates that there exists a correlation gap in the financial market. Consider the same market setting as in Example 3.2, we show how the correlation gap determines the expected excess return for buying the unit-linked insurance product.
In the single period market with
![]() $r=0$
, as in Example 3.2, let us consider a one-period unit-linked insurance product with
$r=0$
, as in Example 3.2, let us consider a one-period unit-linked insurance product with
![]() $T = 1$
. The payout per policy for this unit-linked insurance contract, given by (23), is denoted as
$T = 1$
. The payout per policy for this unit-linked insurance contract, given by (23), is denoted as
![]() $h(1)$
. Assume the threshold
$h(1)$
. Assume the threshold
![]() $K = 300,$
from (24), a market-consistent valuation of this one-period unit-linked insurance product is denoted as
$K = 300,$
from (24), a market-consistent valuation of this one-period unit-linked insurance product is denoted as
![]() $\rho [h(1)]$
and given by:
$\rho [h(1)]$
and given by:
where
![]() $\hat{C}_{\mathbb{Q}}$
represents the time-
$\hat{C}_{\mathbb{Q}}$
represents the time-
![]() $0$
index call option price with strike
$0$
index call option price with strike
![]() $K=300$
and maturity
$K=300$
and maturity
![]() $T=1$
, and
$T=1$
, and
![]() $p_x$
stands for the probability that a policyholder aged exactly
$p_x$
stands for the probability that a policyholder aged exactly
![]() $x$
survives to time
$x$
survives to time
![]() $1$
. Subsequently, the expected excess return for each policyholder at time-
$1$
. Subsequently, the expected excess return for each policyholder at time-
![]() $1$
can be written as:
$1$
can be written as:
where
![]() $S(1)$
is the market index defined in (11).
$S(1)$
is the market index defined in (11).
Using the real-world dynamics in (17), the expectation
![]() $\mathbb{E}^{P}[(S(1) -300)_+]$
can be expressed as follows:
$\mathbb{E}^{P}[(S(1) -300)_+]$
can be expressed as follows:
Additionally, Proposition1 implies that
![]() $\hat{C}_{\mathbb{Q}} = 70+20\rho _{\mathbb{Q}}(1).$
Hence in this market scenario, we can find that:
$\hat{C}_{\mathbb{Q}} = 70+20\rho _{\mathbb{Q}}(1).$
Hence in this market scenario, we can find that:
From (30), we can clearly see that different correlation gaps give rise to different expected excess returns. Indeed, a positive (negative) correlation gap implies a positive (negative) expected excess return for buying the unit-linked insurance. Table 3 compares the expected excess return of the unit-linked insurance policyholder across the three different market scenarios presented in Example 3.2.
Table 3 clearly reveals that the presence of a nonzero correlation gap results in a nonzero expected excess return for the purchase of the unit-linked insurance product. Therefore, a policyholder of the unit-linked insurance contract is also exposed to a correlation risk in the financial market. In the following Section 5, we show how one can trade and hedge the correlation risk in the financial market.
Table 3. Expected excess return for each policyholder in three different market situations

5. Trading the correlation gap
We demonstrated that volatility and correlation under
![]() $\mathbb{P}$
and
$\mathbb{P}$
and
![]() $\mathbb{Q}$
can differ substantially. In this section, we show that the existence of the correlation gap gives rise to trading strategies which have a large expected profit. We will introduce a new financial derivative called dispersion swap, and show that the expected profit for longing the dispersion swap is related to the CRP in the financial market.
$\mathbb{Q}$
can differ substantially. In this section, we show that the existence of the correlation gap gives rise to trading strategies which have a large expected profit. We will introduce a new financial derivative called dispersion swap, and show that the expected profit for longing the dispersion swap is related to the CRP in the financial market.
5.1 Variance swaps
We first introduce a new derivative in our financial market: A variance swap on the stock market index. At maturity
![]() $T,$
the holder of the floating leg of a variance swap receives the difference
$T,$
the holder of the floating leg of a variance swap receives the difference
![]() $ RV[T] -SR[T], $
where
$ RV[T] -SR[T], $
where
![]() $RV[T]$
is defined as:
$RV[T]$
is defined as:
 \begin{equation} RV[T] =\frac{1}{T}\sum _{t=1}^{T} R(t)^2. \end{equation}
\begin{equation} RV[T] =\frac{1}{T}\sum _{t=1}^{T} R(t)^2. \end{equation}
The quantity
![]() $RV[T]$
is called the annualized realized variance and represents the floating leg of the contract. The fixed leg of the contract is
$RV[T]$
is called the annualized realized variance and represents the floating leg of the contract. The fixed leg of the contract is
![]() $SR[T]$
, also called the swap rate. The swap rate of the contract is a constant which is determined at inception such that the contract is fair and no money has to be exchanged at inception. Denote by
$SR[T]$
, also called the swap rate. The swap rate of the contract is a constant which is determined at inception such that the contract is fair and no money has to be exchanged at inception. Denote by
![]() $\mathbb{Q}$
the pricing measure used by the market to price derivatives. The swap rate is then given by:
$\mathbb{Q}$
the pricing measure used by the market to price derivatives. The swap rate is then given by:
The holder of a variance swap will pay the swap rate
![]() $SR[T]$
at maturity and will receive the realized variance
$SR[T]$
at maturity and will receive the realized variance
![]() $RV[T]$
. At time
$RV[T]$
. At time
![]() $0$
, the swap rate is known but the realized variance is random. Meanwhile, investors are willing to pay a premium to hedge against the variance risk in the financial market, called the variance risk premium (VRP); see, e.g., Carr & Wu (Reference Carr and Wu2009), Bollerslev & Zhou (Reference Bollerslev and Zhou2007), and Alibeiki & Lotfaliei (Reference Alibeiki and Lotfaliei2021). Indeed, the VRP is the expected profit for the holder of the variance swap, which is given by:
$0$
, the swap rate is known but the realized variance is random. Meanwhile, investors are willing to pay a premium to hedge against the variance risk in the financial market, called the variance risk premium (VRP); see, e.g., Carr & Wu (Reference Carr and Wu2009), Bollerslev & Zhou (Reference Bollerslev and Zhou2007), and Alibeiki & Lotfaliei (Reference Alibeiki and Lotfaliei2021). Indeed, the VRP is the expected profit for the holder of the variance swap, which is given by:
The VRP can be expressed as follows:
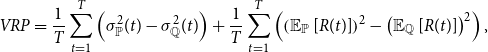 \begin{equation} VRP=\frac{1}{T}\sum _{t=1}^{T}\left ( \sigma _{\mathbb{P}}^{2}(t) -\sigma _{\mathbb{Q}}^{2}(t) \right ) +\frac{1}{T}\sum _{t=1}^{T}\left ( \left ( \mathbb{E}_{\mathbb{P}}\left [ R(t) \right ] \right ) ^{2} - \left ( \mathbb{E}_{\mathbb{Q}}\left [ R(t) \right ] \right ) ^{2} \right ), \end{equation}
\begin{equation} VRP=\frac{1}{T}\sum _{t=1}^{T}\left ( \sigma _{\mathbb{P}}^{2}(t) -\sigma _{\mathbb{Q}}^{2}(t) \right ) +\frac{1}{T}\sum _{t=1}^{T}\left ( \left ( \mathbb{E}_{\mathbb{P}}\left [ R(t) \right ] \right ) ^{2} - \left ( \mathbb{E}_{\mathbb{Q}}\left [ R(t) \right ] \right ) ^{2} \right ), \end{equation}
where
![]() $\sigma _{\mathbb{Q}}(t)$
is the
$\sigma _{\mathbb{Q}}(t)$
is the
![]() $t-$
year forward volatility. Expression (33) clearly shows that the holder of the variance swap longs the real-world volatility and shorts the risk-neutral volatility. The summation in the expression of the VRP arises because a variance swap is actually trading the second moment, rather than the variance. Investing in a variance swap becomes attractive if the gap between real and risk-neutral volatility is substantially large. If this gap is positive, it may lead to a positive VRP, while in the other case, it may yield a negative risk premium. Investors who are exposed to variance risk may be willing to buy the variance swap, even if the risk premium is negative, since it can provide insurance against adverse variance risk scenarios. Indeed, investors who buy the variance swap receive a hedge for their exposure to variance risk and are willing to accept a negative expected profit in return.
$t-$
year forward volatility. Expression (33) clearly shows that the holder of the variance swap longs the real-world volatility and shorts the risk-neutral volatility. The summation in the expression of the VRP arises because a variance swap is actually trading the second moment, rather than the variance. Investing in a variance swap becomes attractive if the gap between real and risk-neutral volatility is substantially large. If this gap is positive, it may lead to a positive VRP, while in the other case, it may yield a negative risk premium. Investors who are exposed to variance risk may be willing to buy the variance swap, even if the risk premium is negative, since it can provide insurance against adverse variance risk scenarios. Indeed, investors who buy the variance swap receive a hedge for their exposure to variance risk and are willing to accept a negative expected profit in return.
5.2 Dispersion swaps
In Example 3.2, it is clear that there exists a correlation gap. However, variance swaps do not allow us to directly trade the difference between the real-world correlation and the implied correlation. Indeed, two prevalent approaches have been proposed for exploiting or hedging the correlation risk within the financial market. First, investors can implement a dispersion trading strategy, wherein they construct a portfolio by taking a position in an index option and the opposite position in the options written on the constituents of the index. Such dispersion strategies have been established using calls, puts, straddles, and variance swaps, see, e.g., Jacquier & Slaoui (Reference Jacquier and Slaoui2007), Bossu (Reference Bossu2014), and Meissner (Reference Meissner2015). In the second approach, one directly trades in correlation derivatives such as correlation swaps or covariance swaps. Correlation swaps were first introduced in the early 2000s as a derivative to hedge against the correlation risk exposure inherent in exotic derivatives trading. However, unlike implied volatility, implied correlations are not directly observable from option markets, making the pricing and hedging of correlation swaps a challenging task. For literature on the pricing of the correlation swap, we refer to Bossu (Reference Bossu2005, Reference Bossu2007). In addition to correlation swaps, covariance swaps are a generalization of the variance swap, providing an alternative method to hedge correlation risk within a two-asset framework. The floating leg of the covariance swap is the realized covariance between the log returns of two underlying assets. Discussions on the pricing and hedging strategies of covariance swaps can be explored in Carr & Corso (Reference Carr and Corso2001) and Salvi & Swishchuk (Reference Salvi and Swishchuk2014).
Instead of employing existing approaches to capitalize on the correlation risk between several assets, we propose a new derivative called the dispersion swap. The floating leg of the contract relies solely on the product of forward returns of the two underlying stocks, establishing an intrinsic link to the correlation between the assets, and simplifying the determination of the fixed leg. Theoretical analysis and numerical results will be presented to demonstrate that the dispersion swap provides an opportunity to trade the correlation gap. Moreover, we also show that the existence of a CRP in the financial market is justified.
The holder of the floating leg of a dispersion swap receives at maturity the following payoff:
where
 \begin{equation} RD[T] =\frac{1}{T}\sum _{t=1}^{T}R_{1}(t) R_{2}(t) . \end{equation}
\begin{equation} RD[T] =\frac{1}{T}\sum _{t=1}^{T}R_{1}(t) R_{2}(t) . \end{equation}
We call
![]() $RD[T]$
the realized dispersion.
$RD[T]$
the realized dispersion.
![]() $P[T]$
is the fixed leg of the contract, determined at inception such that the contract is fair and with zero initial payment. The following proposition is presented to show the realized dispersion can be approximated by the realized variance of stock index and the realized variances of individual stocks. A proof of this proposition can be found in Appendix A.2.
$P[T]$
is the fixed leg of the contract, determined at inception such that the contract is fair and with zero initial payment. The following proposition is presented to show the realized dispersion can be approximated by the realized variance of stock index and the realized variances of individual stocks. A proof of this proposition can be found in Appendix A.2.
Proposition 2. The realized dispersion can be approximated by the difference between the realized variance of the stock market index and the sum of realized stock variances:
where
![]() $RV_i[T]$
is the realized variance for stock
$RV_i[T]$
is the realized variance for stock
![]() $i$
and is given by:
$i$
and is given by:
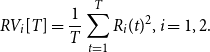 \begin{equation*}RV_i[T] = \frac {1}{T}\sum _{t=1}^{T}R_i(t)^2, i = 1,2.\end{equation*}
\begin{equation*}RV_i[T] = \frac {1}{T}\sum _{t=1}^{T}R_i(t)^2, i = 1,2.\end{equation*}
From Proposition2, the realized dispersion can be approximated by subtracting marginal variances from the basket variance. It implies that the realized dispersion is indeed linked to the dependence. Additionally, there is a more refined approximation approach based on Taylor series expansion, which can be found in Appendix A.5. This approximation allows to determine the approximation error.
At time
![]() $0,$
the realized dispersion is unknown and random, while the strike is fixed and known. The fixed leg
$0,$
the realized dispersion is unknown and random, while the strike is fixed and known. The fixed leg
![]() $P[T]$
is determined as follows:
$P[T]$
is determined as follows:
In our market setting, the fixed leg
![]() $P[T]$
can be expressed as follows:
$P[T]$
can be expressed as follows:
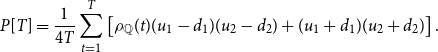 \begin{equation} P[T] =\frac{1}{4T}\sum _{t=1}^{T}\left [\rho _{\mathbb{Q}}(t)(u_1-d_1)(u_2-d_2)+(u_1+d_1)(u_2+d_2)\right ]. \end{equation}
\begin{equation} P[T] =\frac{1}{4T}\sum _{t=1}^{T}\left [\rho _{\mathbb{Q}}(t)(u_1-d_1)(u_2-d_2)+(u_1+d_1)(u_2+d_2)\right ]. \end{equation}
A proof of Expression (36) is given in Appendix A.3.
The expected profit for the holder of the floating leg of a dispersion swap is given by:
Hence it is straightforward to show that the expected profit of the dispersion swap can be expressed as:
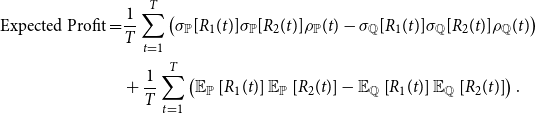 \begin{align} \text{Expected Profit} = & \frac{1}{T}\sum _{t=1}^{T}\left (\sigma _{\mathbb{P}}[R_1(t)]\sigma _{\mathbb{P}}[R_2(t)]\rho _{\mathbb{P}}(t) - \sigma _{\mathbb{Q}}[R_1(t)]\sigma _{\mathbb{Q}}[R_2(t)]\rho _{\mathbb{Q}}(t)\right )\nonumber \\ &+ \frac{1}{T}\sum _{t=1}^{T} \left (\mathbb{E}_{\mathbb{P}}\left [R_1(t)\right ]\mathbb{E}_{\mathbb{P}}\left [R_2(t)\right ]-\mathbb{E}_{\mathbb{Q}}\left [R_1(t)\right ]\mathbb{E}_{\mathbb{Q}}\left [R_2(t)\right ]\right ). \end{align}
\begin{align} \text{Expected Profit} = & \frac{1}{T}\sum _{t=1}^{T}\left (\sigma _{\mathbb{P}}[R_1(t)]\sigma _{\mathbb{P}}[R_2(t)]\rho _{\mathbb{P}}(t) - \sigma _{\mathbb{Q}}[R_1(t)]\sigma _{\mathbb{Q}}[R_2(t)]\rho _{\mathbb{Q}}(t)\right )\nonumber \\ &+ \frac{1}{T}\sum _{t=1}^{T} \left (\mathbb{E}_{\mathbb{P}}\left [R_1(t)\right ]\mathbb{E}_{\mathbb{P}}\left [R_2(t)\right ]-\mathbb{E}_{\mathbb{Q}}\left [R_1(t)\right ]\mathbb{E}_{\mathbb{Q}}\left [R_2(t)\right ]\right ). \end{align}
Expression (37) clearly indicates that the buyer of the dispersion swap longs the real-world correlation and shorts the risk-neutral correlation. To be more specific, in Appendix A.4, it is proven that the expected profit of the dispersion swap can also be written as follows:
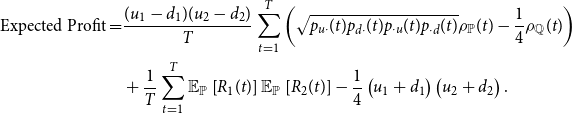 \begin{align} \text{Expected Profit} = &\frac{(u_1-d_1)(u_2-d_2)}{T}\sum _{t=1}^{T}\left (\sqrt{p_{u \cdot }(t)p_{d \cdot }(t)p_{\cdot u}(t)p_{\cdot d}(t)} \rho _{\mathbb{P}}(t)-\nonumber \frac{1}{4}\rho _{\mathbb{Q}}(t)\right )\nonumber \\ & + \frac{1}{T} \sum _{t=1}^{T} \mathbb{E}_{\mathbb{P}}\left [R_1(t)\right ]\mathbb{E}_{\mathbb{P}}\left [R_2(t)\right ] -\frac{1}{4}\left (u_1+d_1\right )\left (u_2+d_2\right ). \end{align}
\begin{align} \text{Expected Profit} = &\frac{(u_1-d_1)(u_2-d_2)}{T}\sum _{t=1}^{T}\left (\sqrt{p_{u \cdot }(t)p_{d \cdot }(t)p_{\cdot u}(t)p_{\cdot d}(t)} \rho _{\mathbb{P}}(t)-\nonumber \frac{1}{4}\rho _{\mathbb{Q}}(t)\right )\nonumber \\ & + \frac{1}{T} \sum _{t=1}^{T} \mathbb{E}_{\mathbb{P}}\left [R_1(t)\right ]\mathbb{E}_{\mathbb{P}}\left [R_2(t)\right ] -\frac{1}{4}\left (u_1+d_1\right )\left (u_2+d_2\right ). \end{align}
From Expressions (37) and (38), we can find that the expected profit of the dispersion swap is closely associated with the correlation gap. The CRP is also defined using the correlation gap. In our market model, the CRP is defined as follows:
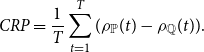 \begin{equation} CRP = \frac{1}{T}\sum _{t=1}^{T} (\rho _{\mathbb{P}}(t) - \rho _{\mathbb{\mathbb{Q}}}(t) ). \end{equation}
\begin{equation} CRP = \frac{1}{T}\sum _{t=1}^{T} (\rho _{\mathbb{P}}(t) - \rho _{\mathbb{\mathbb{Q}}}(t) ). \end{equation}
By assuming the real-world marginals are same as the risk-neutral marginals in this market setting, i.e.,
![]() $p_{u \cdot }\left ( t \right )= p_{\cdot u}\left ( t \right ) =\frac{1}{2},$
the expected profit of the dispersion swap given by (38) can be written as:
$p_{u \cdot }\left ( t \right )= p_{\cdot u}\left ( t \right ) =\frac{1}{2},$
the expected profit of the dispersion swap given by (38) can be written as:
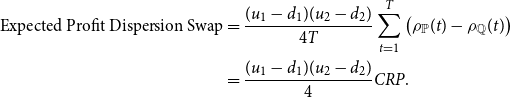 \begin{align} \text{Expected Profit Dispersion Swap} &=\frac{(u_1-d_1)(u_2-d_2)}{4T}\sum _{t=1}^{T}\left (\rho _{\mathbb{P}}(t)- \rho _{\mathbb{Q}}(t)\right )\nonumber \\ &=\frac{(u_1-d_1)(u_2-d_2)}{4} CRP. \end{align}
\begin{align} \text{Expected Profit Dispersion Swap} &=\frac{(u_1-d_1)(u_2-d_2)}{4T}\sum _{t=1}^{T}\left (\rho _{\mathbb{P}}(t)- \rho _{\mathbb{Q}}(t)\right )\nonumber \\ &=\frac{(u_1-d_1)(u_2-d_2)}{4} CRP. \end{align}
When the marginal distributions are the same under
![]() $\mathbb{P}$
and
$\mathbb{P}$
and
![]() $\mathbb{Q}$
, the expected profit of buying the dispersion swap is solely determined by the correlation gap. It is proportional to the CRP, which allows us to directly trade the weighted difference of the correlation gap
$\mathbb{Q}$
, the expected profit of buying the dispersion swap is solely determined by the correlation gap. It is proportional to the CRP, which allows us to directly trade the weighted difference of the correlation gap
![]() $\rho _{\mathbb{P}}(t)- \rho _{\mathbb{Q}}(t)$
. A larger positive correlation gap results in a higher expected profit, increasing the contract’s appeal to potential investors.
$\rho _{\mathbb{P}}(t)- \rho _{\mathbb{Q}}(t)$
. A larger positive correlation gap results in a higher expected profit, increasing the contract’s appeal to potential investors.
5.3 Illustration: One-period example
In this subsection, we still consider the same market setting as in Example 3.2, and will demonstrate the potential use of dispersion swaps in exploiting the correlation gap. In this one-period market with
![]() $r=0$
, it follows directly from the Expression (33) that the expected profit of the variance swap (EPVS) is given by:
$r=0$
, it follows directly from the Expression (33) that the expected profit of the variance swap (EPVS) is given by:
Additionally, the expected profit of the dispersion swap (EPDS) given by Expression (40) can be expressed as follows:
We use Table 4 to compare the expected profits of the variance swap and the dispersion swap, the VRPs and the CRPs, concerning three different market situations in Example 3.2.
In Example 3.2, the first market situation featured a significant gap between the real-world and risk-neutral scenarios. Variance and dispersion swaps serve as tools to exploit this gap. As shown in Table 4, both the VRP and the CRP are positive, suggesting potential benefits from taking long positions in the variance swap and the dispersion swap. However, the gap between the real-world and the risk-neutral volatility and correlation is much smaller in the second market situation, which is reflected in the expected profit of the variance and the dispersion swap, as shown in Table 4. Expected profits turn out to be limited in case. Since these are only expectations, fluctuations can result in losses when stepping in a variance or dispersion trade, making these products less investment-worthy in this market situation than the first market situation. In the third market situation, both the volatility and correlation gaps are strongly negative, resulting in significantly negative variance and CRPs. Rational investors are willing to short the variance swap or the dispersion swap to gain a profit. But who is willing to long the dispersion swap or the variance swap? Market participants who are afraid that the correlation and volatility risk will have significant negative impact on their portfolios are willing to accept a negative expected profit to long the dispersion swap or the variance swap. Indeed, they are more afraid of the correlation and volatility risk than they are of the possible losses from the dispersion and volatility swap.
Table 4. Variance risk premium (VRP) and correlation risk premium (CRP) in three different market situations

6. What are implied measures telling us?
We have shown that risk-neutral and real-world measures can be significantly different, see Example 3.2. Derivative prices reflect the aggregate view of the market about the future dynamics of the stocks involved. Example 3.3 shows that this view can be wrong: while stocks are becoming less dependent over time under the real-world measure, the risk-neutral dependence structure is evolving in the opposite direction; see Table 2 and Fig. 1. In Section 3.2, it seems irrational that the market is pricing a index option with the pricing measure
![]() $\mathbb{Q}^{(1) },$
since
$\mathbb{Q}^{(1) },$
since
![]() $\mathbb{Q}^{(1) }$
has a strong negative dependence structure while the real-world dependence is positive. Is this difference between real-world and risk-neutral dependence a dysfunctioning of the market? This seemingly irrational behavior does not lead to an arbitrage opportunity since the market is incomplete and the risk-neutral probability measure
$\mathbb{Q}^{(1) }$
has a strong negative dependence structure while the real-world dependence is positive. Is this difference between real-world and risk-neutral dependence a dysfunctioning of the market? This seemingly irrational behavior does not lead to an arbitrage opportunity since the market is incomplete and the risk-neutral probability measure
![]() $\mathbb{Q}^{\left (1\right ) }$
belongs to the set
$\mathbb{Q}^{\left (1\right ) }$
belongs to the set
![]() $\mathcal{M}$
of feasible risk-neutral measures; see Theorem1. However, the discrepancy between real-world and risk-neutral correlation provides a trading opportunity. Indeed, the dispersion swap becomes more attractive if the correlation gap becomes larger; see Expression (37). A large correlation gap aligns with a large expected profit.
$\mathcal{M}$
of feasible risk-neutral measures; see Theorem1. However, the discrepancy between real-world and risk-neutral correlation provides a trading opportunity. Indeed, the dispersion swap becomes more attractive if the correlation gap becomes larger; see Expression (37). A large correlation gap aligns with a large expected profit.
We showed that a positive correlation gap corresponds to a positive expected return for longing the dispersion swap, while a negative correlation gap yields a negative expected return. But a positive expected profit does not mean that there is no opportunity for the buyer of the dispersion swap to encounter a loss. Likewise, a negative correlation gap does not imply that investing in the dispersion swap cannot realize any profit at maturity. Consider the one-period setting in Example 3.2, the probability of having a loss for the holder of the floating leg of the dispersion swap is given by:
Expression (43) shows that if the fixed strike
![]() $P[1]$
exceeds the realized dispersion
$P[1]$
exceeds the realized dispersion
![]() $RD[1]$
, the buyer of the dispersion swap incurs a loss. In the one-period setting, realized dispersion
$RD[1]$
, the buyer of the dispersion swap incurs a loss. In the one-period setting, realized dispersion
![]() $R_1(1)R_2(1)$
under the real-world measure
$R_1(1)R_2(1)$
under the real-world measure
![]() $\mathbb{P}$
can take four possible values
$\mathbb{P}$
can take four possible values
![]() $u_1u_2$
,
$u_1u_2$
,
![]() $u_1d_2$
,
$u_1d_2$
,
![]() $d_1u_2$
, or
$d_1u_2$
, or
![]() $d_1d_2$
with corresponding probabilities
$d_1d_2$
with corresponding probabilities
![]() $p_{uu}(1)$
,
$p_{uu}(1)$
,
![]() $p_{ud}(1)$
,
$p_{ud}(1)$
,
![]() $p_{du}(1)$
, and
$p_{du}(1)$
, and
![]() $p_{dd}(1)$
. The fixed leg
$p_{dd}(1)$
. The fixed leg
![]() $P[1]$
is
$P[1]$
is
![]() $\mathbb{E}_{\mathbb{Q}}[R_1(1)R_2(1)]$
. Since all joint probabilities are strictly positive under
$\mathbb{E}_{\mathbb{Q}}[R_1(1)R_2(1)]$
. Since all joint probabilities are strictly positive under
![]() $\mathbb{P}$
, the probability of loss given by (43) is always positive and cannot reach
$\mathbb{P}$
, the probability of loss given by (43) is always positive and cannot reach
![]() $1$
.
$1$
.
Similar to the single period case, the probability of loss when taking the floating leg of the dispersion swap is always positive and less than
![]() $1$
in the multiperiod market. To illustrate this statement, consider
$1$
in the multiperiod market. To illustrate this statement, consider
![]() $T = 10$
. Assume the real-world joint probabilities are given by (20), and
$T = 10$
. Assume the real-world joint probabilities are given by (20), and
![]() $\rho _{\mathbb{P}}(t)\equiv 0.2$
for
$\rho _{\mathbb{P}}(t)\equiv 0.2$
for
![]() $t = 1, 2, \dots, T.$
Two different market situations are specified by implied correlations
$t = 1, 2, \dots, T.$
Two different market situations are specified by implied correlations
![]() $\rho _{\mathbb{Q}^{(1)}}(t) = 0.05t -0.95$
and
$\rho _{\mathbb{Q}^{(1)}}(t) = 0.05t -0.95$
and
![]() $\rho _{\mathbb{Q}^{(2)}}(t) = -0.05t +0.95$
for
$\rho _{\mathbb{Q}^{(2)}}(t) = -0.05t +0.95$
for
![]() $t = 1, 2, \dots, T.$
The following Fig. 2 is presented to show the frequency of different payoffs for the buyer of the dispersion swap in these two different market situations. We can see that in the first market situation, the correlation gap
$t = 1, 2, \dots, T.$
The following Fig. 2 is presented to show the frequency of different payoffs for the buyer of the dispersion swap in these two different market situations. We can see that in the first market situation, the correlation gap
![]() $\rho _{\mathbb{P}}(t) - \rho _{\mathbb{Q}}(t)$
is always assumed to be positive for
$\rho _{\mathbb{P}}(t) - \rho _{\mathbb{Q}}(t)$
is always assumed to be positive for
![]() $t = 1, 2, \dots, T,$
resulting in a positive CRP. Conversely, under
$t = 1, 2, \dots, T,$
resulting in a positive CRP. Conversely, under
![]() $\mathbb{Q}^{(2)}$
, the correlation gap remains negative, yielding a negative CRP. Compare Fig. 2a with b, we can see that the probability of having a loss is larger in the second market situation, and it is because there exists a negative correlation gap in the second market situation. Nevertheless, Fig. 2 shows that the probabilities of taking a loss in the first and the second market situations are both larger than
$\mathbb{Q}^{(2)}$
, the correlation gap remains negative, yielding a negative CRP. Compare Fig. 2a with b, we can see that the probability of having a loss is larger in the second market situation, and it is because there exists a negative correlation gap in the second market situation. Nevertheless, Fig. 2 shows that the probabilities of taking a loss in the first and the second market situations are both larger than
![]() $0$
and smaller than
$0$
and smaller than
![]() $1.$
Due to the possibility of experiencing a loss being nonzero, trading the dispersion swap is not an arbitrage strategy.
$1.$
Due to the possibility of experiencing a loss being nonzero, trading the dispersion swap is not an arbitrage strategy.
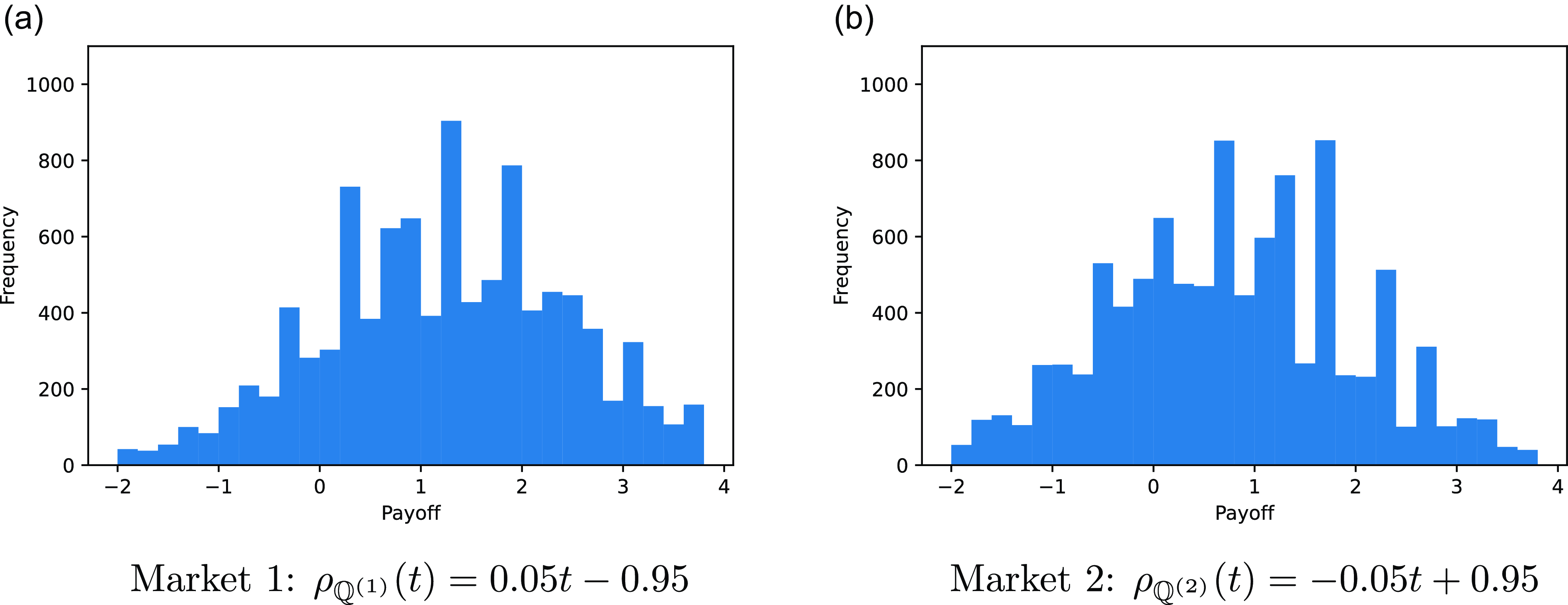
Figure 2 Comparison of payoff histograms for buying the dispersion swap in two market scenarios
![]() $\mathbb{Q}^{(1)}$
and
$\mathbb{Q}^{(1)}$
and
![]() $\mathbb{Q}^{(2)}$
.
$\mathbb{Q}^{(2)}$
.
Throughout the paper, we assumed the probability measure
![]() $\mathbb{P}$
to be known. The knowledge of the real-world dynamics of the stocks enables us to conclude in the example of Section 3.2 that real-world and risk-neutral correlation differ substantially and that entering a dispersion swap results in a positive expected profit. In reality, the probability measure
$\mathbb{P}$
to be known. The knowledge of the real-world dynamics of the stocks enables us to conclude in the example of Section 3.2 that real-world and risk-neutral correlation differ substantially and that entering a dispersion swap results in a positive expected profit. In reality, the probability measure
![]() $\mathbb{P}$
is unknown and subjective: different market participants may have different opinions about the real-world probability measure. The risk-neutral probability measure
$\mathbb{P}$
is unknown and subjective: different market participants may have different opinions about the real-world probability measure. The risk-neutral probability measure
![]() $\mathbb{Q}$
chosen by the market can be extracted unambiguously if sufficient derivative instruments are available. Therefore, it is reasonable to assume that the measure
$\mathbb{Q}$
chosen by the market can be extracted unambiguously if sufficient derivative instruments are available. Therefore, it is reasonable to assume that the measure
![]() $\mathbb{Q}$
is objective in that all market participants agree on the choice of
$\mathbb{Q}$
is objective in that all market participants agree on the choice of
![]() $\mathbb{Q}$
used for pricing derivatives. Consider now the first market situation in the example described in Section 3.2. All market participants observe the same option prices and thus agree that
$\mathbb{Q}$
used for pricing derivatives. Consider now the first market situation in the example described in Section 3.2. All market participants observe the same option prices and thus agree that
![]() $\rho _{\mathbb{Q}^{(1) }}=-0.9.$
In Section 5.3, we then showed that an investor using
$\rho _{\mathbb{Q}^{(1) }}=-0.9.$
In Section 5.3, we then showed that an investor using
![]() $\rho _{\mathbb{P}}=0.2$
may want to invest in the floating leg of a dispersion swap since this gives the investor a positive expected profit. Consider now another investor, who uses another real-world measure
$\rho _{\mathbb{P}}=0.2$
may want to invest in the floating leg of a dispersion swap since this gives the investor a positive expected profit. Consider now another investor, who uses another real-world measure
![]() $\mathbb{P}^{\prime }$
and believes that
$\mathbb{P}^{\prime }$
and believes that
![]() $\rho _{\mathbb{P}^{\prime }}=-0.95.$
This investor may want to take the fixed leg of a dispersion swap since this produces a positive expected profit. Both investors are observing the same option prices, but have different opinions about the real-world measure. They both observe a correlation gap and consider a dispersion swap to exploit this gap. They do agree on the value of the fixed leg of the dispersion swap since the risk-neutral measure is assumed to be objective. However, they have different opinions about the sign of the correlation gap. As a result, they both agree to enter in a trade, where each one takes a side of the same dispersion swap.
$\rho _{\mathbb{P}^{\prime }}=-0.95.$
This investor may want to take the fixed leg of a dispersion swap since this produces a positive expected profit. Both investors are observing the same option prices, but have different opinions about the real-world measure. They both observe a correlation gap and consider a dispersion swap to exploit this gap. They do agree on the value of the fixed leg of the dispersion swap since the risk-neutral measure is assumed to be objective. However, they have different opinions about the sign of the correlation gap. As a result, they both agree to enter in a trade, where each one takes a side of the same dispersion swap.
Note that if the real-world measure is also objective, all market participants would see the same correlation gap. For example, consider market situation 1 in the example described in Section 3.2. All market participants agree that
![]() $\rho _{\mathbb{P}}=0.2,$
so most investors want to enter the floating leg of a dispersion swap, i.e. there is a larger number of individuals willing to receive the realized dispersion and pay the fixed leg than there are market participants willing to take up the opposite leg of the dispersion swap. Therefore, this imbalance between supply and demand will push the implied correlation to increase toward the realized correlation.
$\rho _{\mathbb{P}}=0.2,$
so most investors want to enter the floating leg of a dispersion swap, i.e. there is a larger number of individuals willing to receive the realized dispersion and pay the fixed leg than there are market participants willing to take up the opposite leg of the dispersion swap. Therefore, this imbalance between supply and demand will push the implied correlation to increase toward the realized correlation.
However, will the correlation gap converge to
![]() $0$
eventually? To answer this question, we shift to the market situation 3 in Section 3.2. In this market situation, the implied correlation
$0$
eventually? To answer this question, we shift to the market situation 3 in Section 3.2. In this market situation, the implied correlation
![]() $\rho _{\mathbb{Q}^{(3)}}(t)$
equals
$\rho _{\mathbb{Q}^{(3)}}(t)$
equals
![]() $0.8$
, and the real-world correlation is still
$0.8$
, and the real-world correlation is still
![]() $0.2$
. It follows directly that the correlation gap in this market is negative. Moreover, the probability of taking a loss for buying the dispersion swap is equal to 0.7. Therefore, many investors are consequently willing to short the dispersion swap. However, there are still investors willing to long the dispersion swap, since they dislike the correlation risk in the financial market and would like to offset their correlation exposure. Investing in the dispersion swap can offer a hedge against the correlation increases.
$0.2$
. It follows directly that the correlation gap in this market is negative. Moreover, the probability of taking a loss for buying the dispersion swap is equal to 0.7. Therefore, many investors are consequently willing to short the dispersion swap. However, there are still investors willing to long the dispersion swap, since they dislike the correlation risk in the financial market and would like to offset their correlation exposure. Investing in the dispersion swap can offer a hedge against the correlation increases.
Ultimately, the market may attain a state of equilibrium with a negative CRP. To be more precise, if there are more investors selling the dispersion swap than buying the dispersion swap in this market situation, the negative correlation gap will gradually tighten. It will reach an equilibrium when the number of sellers in the dispersion swap contract aligns with the number of buyers. Indeed, when the CRP comes closer to zero, a short position in the dispersion swap still has a positive expected profit, but becomes less attractive due to an increase in the probability of a loss. At the same time, hedging correlation risk through the dispersion swap becomes more attractive. Therefore, with a tightening of the correlation gap, the number of people who would like to short the dispersion swap decreases whereas the number of people who are inclined to hedge the correlation risk increases. At some point, the number of sellers of the dispersion swap will match the number of buyers to reach a market equilibrium. At this equilibrium, the CRP can still be strictly negative. Indeed, in such a situation, market participants looking for hedging their correlation risk are willing to pay a premium to offset this risk, whereas the increased probability of a loss when shorting the dispersion swap limits the supply of correlation hedges through the dispersion swap. Consequently, this situation explains the negative CRP which is often observed in the market.
7. Conclusion
This paper showed that risk-neutral dependence can significantly diverge from real-world dependence when working in an incomplete two-dimensional market model. We characterized the set of equivalent martingale measures and illustrated the correlation gap between
![]() $\mathbb{P}$
and
$\mathbb{P}$
and
![]() $\mathbb{Q}$
. A unit-linked insurance product was considered to illustrate that this nonzero correlation gap also exerts influence on the expected excess return for policyholders. We also introduced the dispersion swap to exploit the correlation gap. Both theoretical and numerical results were provided to illustrate that the dispersion swap serves not only as a tool to capitalize on the large correlation gap, but also as a hedging strategy for the correlation risk in the financial market.
$\mathbb{Q}$
. A unit-linked insurance product was considered to illustrate that this nonzero correlation gap also exerts influence on the expected excess return for policyholders. We also introduced the dispersion swap to exploit the correlation gap. Both theoretical and numerical results were provided to illustrate that the dispersion swap serves not only as a tool to capitalize on the large correlation gap, but also as a hedging strategy for the correlation risk in the financial market.
We also demonstrated that investors with strong fear of correlation risk are willing to take long positions in the dispersion swap, even when the expected profit is negative. As a consequence, the market will reach an equilibrium with a negative CRP.
Acknowledgements
The authors acknowledge the FWO Scientific Research Network ModSimFIE (FWO WOG W001021N). Jan Dhaene, Daniël Linders, and Biwen Ling acknowledge the financial support of KU Leuven Research Council (BOF) under grant C14/21/089. Jan Dhaene also acknowledges the funding from FWO and F.R.S.-FNRS under the Excellence of Science (EOS) programme, project ASTeRISK (40007517). Additionally, the authors would like to thank the anonymous reviewers for their valuable feedback to improve the paper.
Data availability statement
The Python code for reproducing our numerical results can be accessed at the following GitHub repository: https://github.com/BiwenLing/Understanding_CRP.
Competing interests
The authors have no competing interests to declare.
A. Proofs and calculations
A.1 Proof of Theorem1
We first take into account the martingale condition. For any
![]() $t$
, we find that the risk-neutral marginal probabilities
$t$
, we find that the risk-neutral marginal probabilities
![]() $\left (q_{d \cdot }\left (t \right ), q_{u \cdot }\left (t \right ), q_{\cdot u}(t), q_{\cdot d}\left (t\right ) \right )$
satisfy:
$\left (q_{d \cdot }\left (t \right ), q_{u \cdot }\left (t \right ), q_{\cdot u}(t), q_{\cdot d}\left (t\right ) \right )$
satisfy:
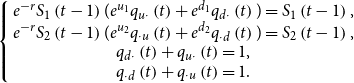 \begin{equation} \left \{ \begin{array} [c]{c}e^{-r}S_1\left (t-1\right )(e^{u_1} q_{u \cdot }\left (t\right )+e^{d_1} q_{d \cdot }\left (t \right )) =S_1\left (t-1\right ),\\ e^{-r}S_2\left (t-1\right )(e^{u_2} q_{\cdot u}\left (t\right )+e^{d_2} q_{\cdot d}\left (t \right )) =S_2\left (t-1\right ),\\ q_{d \cdot }\left (t \right )+q_{u \cdot }\left (t \right )=1,\\ q_{\cdot d}\left (t \right )+q_{\cdot u}\left (t \right )=1. \end{array} \right . \end{equation}
\begin{equation} \left \{ \begin{array} [c]{c}e^{-r}S_1\left (t-1\right )(e^{u_1} q_{u \cdot }\left (t\right )+e^{d_1} q_{d \cdot }\left (t \right )) =S_1\left (t-1\right ),\\ e^{-r}S_2\left (t-1\right )(e^{u_2} q_{\cdot u}\left (t\right )+e^{d_2} q_{\cdot d}\left (t \right )) =S_2\left (t-1\right ),\\ q_{d \cdot }\left (t \right )+q_{u \cdot }\left (t \right )=1,\\ q_{\cdot d}\left (t \right )+q_{\cdot u}\left (t \right )=1. \end{array} \right . \end{equation}
From (44), we find that the marginal probabilities are independent of the time, hence the risk-neutral marginal probabilities can be denoted as
![]() $(q_{d \cdot }, q_{u \cdot }, q_{\cdot d}, q_{\cdot u})$
, and are given by:
$(q_{d \cdot }, q_{u \cdot }, q_{\cdot d}, q_{\cdot u})$
, and are given by:
Notice we can write
![]() $q_{uu}(t) =\mathbb{Q}\left [ R_{2}(t) =u_2\mid R_{1}(t) =u_1\right ] \times \mathbb{Q}\left [ R_{1}(t) =u_1\right ].$
We use
$q_{uu}(t) =\mathbb{Q}\left [ R_{2}(t) =u_2\mid R_{1}(t) =u_1\right ] \times \mathbb{Q}\left [ R_{1}(t) =u_1\right ].$
We use
![]() $\alpha _{\mathbb{Q}}(t)$
to denote
$\alpha _{\mathbb{Q}}(t)$
to denote
![]() $\mathbb{Q}\left [ R_{2}(t) =u_2\mid R_{1}(t) =u_1\right ]$
, and taking into account Expressions (45), we find that
$\mathbb{Q}\left [ R_{2}(t) =u_2\mid R_{1}(t) =u_1\right ]$
, and taking into account Expressions (45), we find that
![]() $ q_{uu}(t) =\frac{\alpha (t) }{2}.$
Similarly, expressions can be derived for
$ q_{uu}(t) =\frac{\alpha (t) }{2}.$
Similarly, expressions can be derived for
![]() $q_{ud}(t),q_{du}(t)$
and
$q_{ud}(t),q_{du}(t)$
and
![]() $q_{dd}(t).$
Hence the set
$q_{dd}(t).$
Hence the set
![]() $\mathcal{M}$
of feasible risk-neutral probability measure can be characterized as follows:
$\mathcal{M}$
of feasible risk-neutral probability measure can be characterized as follows:
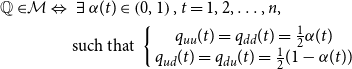 \begin{align} \mathbb{Q\in }\mathcal{M\Leftrightarrow }\text{ } & \text{ }\exists \text{ }\alpha (t)\in \left ( 0,1\right ), t=1,2,\ldots, n,\nonumber \\ & \text{such that }\left \{ \begin{array} [c]{c}q_{u u}(t)= q_{d d}(t) = \frac{1}{2}\alpha (t)\\ q_{u d}(t)= q_{d u}(t) = \frac{1}{2}(1-\alpha (t)) \end{array} \right . \end{align}
\begin{align} \mathbb{Q\in }\mathcal{M\Leftrightarrow }\text{ } & \text{ }\exists \text{ }\alpha (t)\in \left ( 0,1\right ), t=1,2,\ldots, n,\nonumber \\ & \text{such that }\left \{ \begin{array} [c]{c}q_{u u}(t)= q_{d d}(t) = \frac{1}{2}\alpha (t)\\ q_{u d}(t)= q_{d u}(t) = \frac{1}{2}(1-\alpha (t)) \end{array} \right . \end{align}
Since
![]() $\mathbb{Q}$
has to be equivalent to
$\mathbb{Q}$
has to be equivalent to
![]() $\mathbb{P}$
, we need that
$\mathbb{P}$
, we need that
![]() $p_{uu}(t), p_{ud}(t), p_{du}(t), p_{dd}(t) \gt 0.$
Hence we find that
$p_{uu}(t), p_{ud}(t), p_{du}(t), p_{dd}(t) \gt 0.$
Hence we find that
![]() $\alpha (t)\in \left ( 0,1\right ) .$
$\alpha (t)\in \left ( 0,1\right ) .$
The risk-neutral covariance
![]() $\text{Cov}_{\mathbb{Q}}\left [ R_{1}(t), R_{2}(t) \right ]$
can be determined as follows:
$\text{Cov}_{\mathbb{Q}}\left [ R_{1}(t), R_{2}(t) \right ]$
can be determined as follows:
We then find:
A.2 Proof of Proposition2
First, the forward return of the stock market index at time
![]() $t_i$
can be expressed as:
$t_i$
can be expressed as:
By replacing
![]() $S_1(t-1)S_1(t)S_2(t-1)$
by
$S_1(t-1)S_1(t)S_2(t-1)$
by
![]() $S_1(t-1)S_1(t)S_2(t)$
and replacing
$S_1(t-1)S_1(t)S_2(t)$
and replacing
![]() $S_1(t-1)S_2(t-1)S_2(t)$
by
$S_1(t-1)S_2(t-1)S_2(t)$
by
![]() $S_1(t)S_2(t-1)S_2(t)$
,
$S_1(t)S_2(t-1)S_2(t)$
,
![]() $R(t)$
can be approximated by:
$R(t)$
can be approximated by:
It follows directly the realized dispersion can be approximated by (35).
A.3 Proof of expression (36)
It follows from (5) directly that the fixed leg
![]() $P[T]$
can be written as follows:
$P[T]$
can be written as follows:
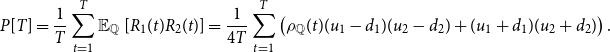 \begin{equation*} P[T] =\frac {1}{T}\sum _{t=1}^{T}\mathbb {E}_{\mathbb {Q}}\left [ R_{1}(t) R_{2}(t) \right ] = \frac {1}{4T}\sum _{t=1}^{T}\left (\rho _{\mathbb {Q}}(t)(u_1-d_1)(u_2-d_2)+(u_1+d_1)(u_2+d_2)\right ). \end{equation*}
\begin{equation*} P[T] =\frac {1}{T}\sum _{t=1}^{T}\mathbb {E}_{\mathbb {Q}}\left [ R_{1}(t) R_{2}(t) \right ] = \frac {1}{4T}\sum _{t=1}^{T}\left (\rho _{\mathbb {Q}}(t)(u_1-d_1)(u_2-d_2)+(u_1+d_1)(u_2+d_2)\right ). \end{equation*}
A.4 Proof of expression (37)
Note that
![]() $\mathbb{E}_{\mathbb{P}}\left [ R_{1}(t) R_{2}(t) \right ]$
can be expressed as:
$\mathbb{E}_{\mathbb{P}}\left [ R_{1}(t) R_{2}(t) \right ]$
can be expressed as:
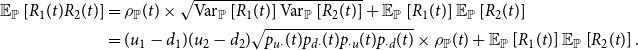 \begin{align*} \mathbb{E}_{\mathbb{P}}\left [ R_{1}(t) R_{2}(t) \right ] &=\rho _{\mathbb{P}}(t)\times \sqrt{\text{Var}_{\mathbb{P}}\left [ R_{1}(t) \right ] \text{Var}_{\mathbb{P}}\left [ R_{2}(t) \right ] }+\mathbb{E}_{\mathbb{P}}\left [ R_{1}(t) \right ] \mathbb{E}_{\mathbb{P}}\left [ R_{2}(t) \right ]\\ &= (u_1-d_1)(u_2-d_2)\sqrt{p_{u \cdot }(t)p_{d \cdot }(t)p_{\cdot u}(t)p_{\cdot d}(t)}\times \rho _{\mathbb{P}}(t)+\mathbb{E}_{\mathbb{P}}\left [ R_{1}(t) \right ] \mathbb{E}_{\mathbb{P}}\left [ R_{2}(t) \right ]. \end{align*}
\begin{align*} \mathbb{E}_{\mathbb{P}}\left [ R_{1}(t) R_{2}(t) \right ] &=\rho _{\mathbb{P}}(t)\times \sqrt{\text{Var}_{\mathbb{P}}\left [ R_{1}(t) \right ] \text{Var}_{\mathbb{P}}\left [ R_{2}(t) \right ] }+\mathbb{E}_{\mathbb{P}}\left [ R_{1}(t) \right ] \mathbb{E}_{\mathbb{P}}\left [ R_{2}(t) \right ]\\ &= (u_1-d_1)(u_2-d_2)\sqrt{p_{u \cdot }(t)p_{d \cdot }(t)p_{\cdot u}(t)p_{\cdot d}(t)}\times \rho _{\mathbb{P}}(t)+\mathbb{E}_{\mathbb{P}}\left [ R_{1}(t) \right ] \mathbb{E}_{\mathbb{P}}\left [ R_{2}(t) \right ]. \end{align*}
Then we can derive the expected profit of the dispersion swap:
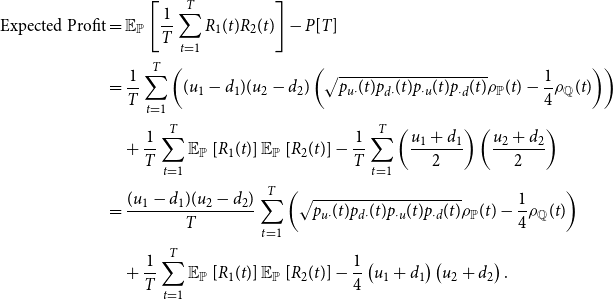 \begin{align*} \text{Expected Profit} &= \mathbb{E}_{\mathbb{P}}\left [\frac{1}{T}\sum _{t=1}^{T}R_{1}(t) R_{2}(t)\right ] - P[T]\\ &=\frac{1}{T}\sum _{t=1}^{T}\left ((u_1-d_1)(u_2-d_2)\left (\sqrt{p_{u \cdot }(t)p_{d \cdot }(t)p_{\cdot u}(t)p_{\cdot d}(t)} \rho _{\mathbb{P}}(t)-\frac{1}{4} \rho _{\mathbb{Q}}(t)\right )\right )\\ &\quad + \frac{1}{T} \sum _{t=1}^{T}\mathbb{E}_{\mathbb{P}}\left [ R_{1}(t) \right ] \mathbb{E}_{\mathbb{P}}\left [ R_{2}(t) \right ] - \frac{1}{T} \sum _{t=1}^{T} \left (\frac{u_1+d_1}{2}\right )\left (\frac{u_2+d_2}{2}\right )\\ &= \frac{(u_1-d_1)(u_2-d_2)}{T}\sum _{t=1}^{T}\left (\sqrt{p_{u \cdot }(t)p_{d \cdot }(t)p_{\cdot u}(t)p_{\cdot d}(t)} \rho _{\mathbb{P}}(t)-\frac{1}{4}\rho _{\mathbb{Q}}(t)\right )\\ &\quad + \frac{1}{T} \sum _{t=1}^{T} \mathbb{E}_{\mathbb{P}}\left [R_1(t)\right ]\mathbb{E}_{\mathbb{P}}\left [R_2(t)\right ] -\frac{1}{4}\left (u_1+d_1\right )\left (u_2+d_2\right ). \end{align*}
\begin{align*} \text{Expected Profit} &= \mathbb{E}_{\mathbb{P}}\left [\frac{1}{T}\sum _{t=1}^{T}R_{1}(t) R_{2}(t)\right ] - P[T]\\ &=\frac{1}{T}\sum _{t=1}^{T}\left ((u_1-d_1)(u_2-d_2)\left (\sqrt{p_{u \cdot }(t)p_{d \cdot }(t)p_{\cdot u}(t)p_{\cdot d}(t)} \rho _{\mathbb{P}}(t)-\frac{1}{4} \rho _{\mathbb{Q}}(t)\right )\right )\\ &\quad + \frac{1}{T} \sum _{t=1}^{T}\mathbb{E}_{\mathbb{P}}\left [ R_{1}(t) \right ] \mathbb{E}_{\mathbb{P}}\left [ R_{2}(t) \right ] - \frac{1}{T} \sum _{t=1}^{T} \left (\frac{u_1+d_1}{2}\right )\left (\frac{u_2+d_2}{2}\right )\\ &= \frac{(u_1-d_1)(u_2-d_2)}{T}\sum _{t=1}^{T}\left (\sqrt{p_{u \cdot }(t)p_{d \cdot }(t)p_{\cdot u}(t)p_{\cdot d}(t)} \rho _{\mathbb{P}}(t)-\frac{1}{4}\rho _{\mathbb{Q}}(t)\right )\\ &\quad + \frac{1}{T} \sum _{t=1}^{T} \mathbb{E}_{\mathbb{P}}\left [R_1(t)\right ]\mathbb{E}_{\mathbb{P}}\left [R_2(t)\right ] -\frac{1}{4}\left (u_1+d_1\right )\left (u_2+d_2\right ). \end{align*}
A.5 Approximation of the realized dispersion: Taylor series expansion
Proposition 3. The realized dispersion can be approximated by the difference between the realized variance of the stock market index and a weighted sum of realized stock variances:
 \begin{equation} RD[T] = \frac{1}{T} \sum _{t=1}^{T} \frac{R(t)^2 - w_1(t-1)^2R_1(t)^2 - w_2(t-1)^2R_2(t)^2}{2w_1(t-1)w_2(t-1)} + \epsilon, \end{equation}
\begin{equation} RD[T] = \frac{1}{T} \sum _{t=1}^{T} \frac{R(t)^2 - w_1(t-1)^2R_1(t)^2 - w_2(t-1)^2R_2(t)^2}{2w_1(t-1)w_2(t-1)} + \epsilon, \end{equation}
where
and
![]() $\epsilon$
represents the approximation error given by:
$\epsilon$
represents the approximation error given by:
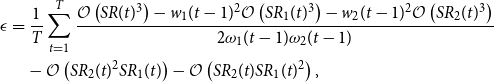 \begin{align} \epsilon &= \frac{1}{T}\sum _{t=1}^T \frac{\mathcal{O}\left (SR(t)^3\right ) - w_1(t-1)^2\mathcal{O}\left (SR_1(t)^3\right ) - w_2(t-1)^2\mathcal{O}\left (SR_2(t)^3\right )}{2\omega _1(t-1)\omega _2(t-1)}\\ &\quad -\mathcal{O}\left (SR_2(t)^2SR_1(t)\right )- \mathcal{O}\left (SR_2(t)SR_1(t)^2\right )\nonumber, \end{align}
\begin{align} \epsilon &= \frac{1}{T}\sum _{t=1}^T \frac{\mathcal{O}\left (SR(t)^3\right ) - w_1(t-1)^2\mathcal{O}\left (SR_1(t)^3\right ) - w_2(t-1)^2\mathcal{O}\left (SR_2(t)^3\right )}{2\omega _1(t-1)\omega _2(t-1)}\\ &\quad -\mathcal{O}\left (SR_2(t)^2SR_1(t)\right )- \mathcal{O}\left (SR_2(t)SR_1(t)^2\right )\nonumber, \end{align}
and
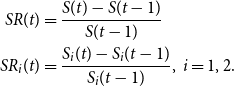 \begin{align*} SR(t) &= \frac{S(t)-S(t-1)}{S(t-1)}\\ SR_i(t)&= \frac{S_i(t)-S_i(t-1)}{S_i(t-1)}, \ i=1,2. \end{align*}
\begin{align*} SR(t) &= \frac{S(t)-S(t-1)}{S(t-1)}\\ SR_i(t)&= \frac{S_i(t)-S_i(t-1)}{S_i(t-1)}, \ i=1,2. \end{align*}
Proof.
First, the square of the index forward return at time
![]() $t$
is given by:
$t$
is given by:
Consider a function
![]() $f(x) = \left (\log (1+x)\right )^2$
, we use the first two terms of the Taylor series expansion to approximate
$f(x) = \left (\log (1+x)\right )^2$
, we use the first two terms of the Taylor series expansion to approximate
![]() $f(x)$
centered at
$f(x)$
centered at
![]() $x=0$
which gives
$x=0$
which gives
![]() $ f(x) = x^2 + \mathcal{O}(x^3),$
where
$ f(x) = x^2 + \mathcal{O}(x^3),$
where
![]() $\mathcal{O}(x^3)$
represents the approximation error. Hence the approximation of
$\mathcal{O}(x^3)$
represents the approximation error. Hence the approximation of
![]() $R(t)^2$
is given by:
$R(t)^2$
is given by:
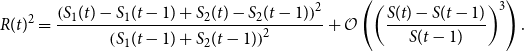 \begin{align} R(t)^2 &= \frac{\left (S_1(t) - S_1(t-1) + S_2(t) - S_2(t-1)\right )^2}{\left (S_1(t-1) + S_2(t-1)\right )^2} + \mathcal{O}\left (\left (\frac{S(t)-S(t-1)}{S(t-1)}\right )^3\right ). \end{align}
\begin{align} R(t)^2 &= \frac{\left (S_1(t) - S_1(t-1) + S_2(t) - S_2(t-1)\right )^2}{\left (S_1(t-1) + S_2(t-1)\right )^2} + \mathcal{O}\left (\left (\frac{S(t)-S(t-1)}{S(t-1)}\right )^3\right ). \end{align}
Similarly, we approximate the square of individual stock forward returns by the following expressions:
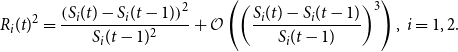 \begin{align} R_i(t)^2 &= \frac{\left (S_i(t) - S_i(t-1)\right )^2}{S_i(t-1)^2}+ \mathcal{O}\left (\left (\frac{S_i(t)-S_i(t-1)}{S_i(t-1)}\right )^3\right ), \ i=1,2. \end{align}
\begin{align} R_i(t)^2 &= \frac{\left (S_i(t) - S_i(t-1)\right )^2}{S_i(t-1)^2}+ \mathcal{O}\left (\left (\frac{S_i(t)-S_i(t-1)}{S_i(t-1)}\right )^3\right ), \ i=1,2. \end{align}
Meanwhile, the forward return of stock 1 at time
![]() $t$
is given by:
$t$
is given by:
Consider another function
![]() $g(x) = \log (1+x)$
, we approximate
$g(x) = \log (1+x)$
, we approximate
![]() $g(x)$
by using the first term of the Taylor series expansion of
$g(x)$
by using the first term of the Taylor series expansion of
![]() $g(x)$
centered at
$g(x)$
centered at
![]() $x=0$
to obtain
$x=0$
to obtain
![]() $g(x) = x + \mathcal{O}(x^2).$
Then
$g(x) = x + \mathcal{O}(x^2).$
Then
![]() $R_1(t)R_2(t)$
can be approximated by:
$R_1(t)R_2(t)$
can be approximated by:
 \begin{align} R_1(t)R_2(t) =&\prod _{i=1}^2\left ( \frac{S_i(t) - S_i(t-1)}{S_i(t-1)} + \mathcal{O}\left (\left (\frac{S_i(t)-S_i(t-1)}{S_i(t-1)}\right )^2\right )\right ). \end{align}
\begin{align} R_1(t)R_2(t) =&\prod _{i=1}^2\left ( \frac{S_i(t) - S_i(t-1)}{S_i(t-1)} + \mathcal{O}\left (\left (\frac{S_i(t)-S_i(t-1)}{S_i(t-1)}\right )^2\right )\right ). \end{align}
From Expressions (50), (51), and (52), we find that the realized dispersion can be approximated by Expression (47). We can find that
![]() $w_1(t-1)$
and
$w_1(t-1)$
and
![]() $w_2(t-1)$
are the relative importance of stock 1 and stock 2 in the market index
$w_2(t-1)$
are the relative importance of stock 1 and stock 2 in the market index
![]() $S(t-1)$
, respectively.
$S(t-1)$
, respectively.













