Article contents
An optimal multi-layer reinsurance policy under conditional tail expectation
Published online by Cambridge University Press: 26 July 2017
Abstract
An usual reinsurance policy for insurance companies admits one or two layers of the payment deductions. Under optimality criterion of minimising the Conditional Tail Expectation (CTE) risk measure of the insurer’s total risk, this article generalises an optimal stop-loss reinsurance policy to an optimal multi-layer reinsurance policy. To achieve such optimal multi-layer reinsurance policy, this article starts from a given optimal stop-loss reinsurance policy f(⋅). In the first step, it cuts down the interval [0, ∞) into intervals [0, M 1) and [M 1, ∞). By shifting the origin of Cartesian coordinate system to (M 1, f(M 1)), and showing that under the CTE criteria 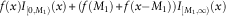 $$f\left( x \right)I_{{[0,M_{{\rm 1}} )}} \left( x \right){\plus}\left( {f\left( {M_{{\rm 1}} } \right){\plus}f\left( {x{\minus}M_{{\rm 1}} } \right)} \right)I_{{[M_{{\rm 1}} ,{\rm }\infty)}} \left( x \right)$$ is, again, an optimal policy. This extension procedure can be repeated to obtain an optimal k-layer reinsurance policy. Finally, unknown parameters of the optimal multi-layer reinsurance policy are estimated using some additional appropriate criteria. Three simulation-based studies have been conducted to demonstrate: (1) the practical applications of our findings and (2) how one may employ other appropriate criteria to estimate unknown parameters of an optimal multi-layer contract. The multi-layer reinsurance policy, similar to the original stop-loss reinsurance policy is optimal, in a same sense. Moreover, it has some other optimal criteria which the original policy does not have. Under optimality criterion of minimising a general translative and monotone risk measure ρ(⋅) of either the insurer’s total risk or both the insurer’s and the reinsurer’s total risks, this article (in its discussion) also extends a given optimal reinsurance contract f(⋅) to a multi-layer and continuous reinsurance policy.
$$f\left( x \right)I_{{[0,M_{{\rm 1}} )}} \left( x \right){\plus}\left( {f\left( {M_{{\rm 1}} } \right){\plus}f\left( {x{\minus}M_{{\rm 1}} } \right)} \right)I_{{[M_{{\rm 1}} ,{\rm }\infty)}} \left( x \right)$$ is, again, an optimal policy. This extension procedure can be repeated to obtain an optimal k-layer reinsurance policy. Finally, unknown parameters of the optimal multi-layer reinsurance policy are estimated using some additional appropriate criteria. Three simulation-based studies have been conducted to demonstrate: (1) the practical applications of our findings and (2) how one may employ other appropriate criteria to estimate unknown parameters of an optimal multi-layer contract. The multi-layer reinsurance policy, similar to the original stop-loss reinsurance policy is optimal, in a same sense. Moreover, it has some other optimal criteria which the original policy does not have. Under optimality criterion of minimising a general translative and monotone risk measure ρ(⋅) of either the insurer’s total risk or both the insurer’s and the reinsurer’s total risks, this article (in its discussion) also extends a given optimal reinsurance contract f(⋅) to a multi-layer and continuous reinsurance policy.
Keywords
Information
- Type
- Papers
- Information
- Copyright
- © Institute and Faculty of Actuaries 2017
References
- 2
- Cited by

