Introduction
Lamb birth weight has long been considered a major risk factor for lamb viability and survival (Gama et al., Reference Gama, Dickerson, Young and Leymaster1991; Christley et al., Reference Christley, Morgan, Parkin and French2003), extreme birth weights being highly related to substantial increases in lamb mortality (Christley et al., Reference Christley, Morgan, Parkin and French2003; Casellas et al., Reference Casellas, Caja, Such and Piedrafita2007c). Birth weight plays a central role in body temperature regulation with significant influences on lamb behaviour and metabolism (Dwyer and Morgan, Reference Dwyer and Morgan2006). Although genetic and environmental factors influencing birth weight have been widely analysed, no studies have addressed the genetic aspects of within-litter birth weight variation (BWV) in lambs. Previous research in other prolific species like mice (Van Engelen et al., Reference Van Engelen, Nielsen and Ribeiro EL de1995), pigs (Högberg and Rydhmer, Reference Högberg and Rydhmer2000; Damgaard et al., Reference Damgaard, Rydhmer, Løvendahl and Grandinson2003) and rabbits (Garreau et al., Reference Garreau, Bolet, Hurtaud, Larzul, Robert-Granié, Ros, Saleil, SanCristobal and Bodin2004) suggested that selection for survivability could reduce BWV (Knol, Reference Knol2001; Garreau et al., Reference Garreau, Bolet, Hurtaud, Larzul, Robert-Granié, Ros, Saleil, SanCristobal and Bodin2004). Within this context, lamb within-litter birth weight variation could become an appealing future survival criterion for sheep selection programmes in which litter size at birth (LS) is a main objective, although the genetic knowledge about this trait is very limited in sheep.
Litter size and litter weight (LW) at birth are two of the most important productive traits in meat sheep (Olesen et al., Reference Olesen, Pérez-Enciso, Gianola and Thomas1994; Freetly and Leymaster, Reference Freetly and Leymaster2004) and selection programmes are commonly focused on LS (Bhuiyan and Curran, Reference Bhuiyan and Curran1993; Casellas et al., Reference Casellas, Caja, Ferret and Piedrafita2007b). Nevertheless, little is known about correlated effects on LW and BWV. Positive genetic and residual correlations have been suggested between LS and BWV in pigs (Damgaard et al., Reference Damgaard, Rydhmer, Løvendahl and Grandinson2003) but we lack comparable results in sheep. The objective of this study was to ascertain whether additive genetic variance exists for within-litter BWV in lamb weight at birth. Further objectives were to estimate genetic, permanent environmental and residual correlations between BWV, LW and LS in sheep, as well as the relation between BWV and lamb survival.
Material and methods
Ripollesa breed
The Ripollesa is a medium-sized sheep (ewes, 50 to 65 kg live weight; rams, 75 to 90 kg live weight) and the most abundant native ovine breed in Catalonia, the north-east region of Spain (Guillaumet and Caja, Reference Guillaumet and Caja2001; Milán et al., Reference Milán, Arnalte and Caja2003). Although with an unclear origin, this breed seems to derive from the crossbreeding of transhumant Merino individuals and the native ovine population of the Pyrenees Mountains (Torre, Reference Torre1991), and has been related with the Spanish ‘entrefino’ trunk (Sánchez Belda and Sánchez Trujillano, Reference Sánchez Belda and Sánchez Trujillano1986). Purebred animals are white with dark brown or black marks on the head and legs and with white wool and closed fleece (fibre diameter, 23 to 26 μm). The Ripollesa sheep is exploited under semi-intensive Mediterranean conditions for the production of ‘Pascual-type’ lambs (22 to 24 kg live weight at slaughter; Guillaumet and Caja, Reference Guillaumet and Caja2001) with an average mortality until slaughter of approximately 10% (Casellas et al., Reference Casellas, Caja, Such and Piedrafita2007c). Ripollesa breed is usually considered as a low prolific breed (1.2 lambs per birth; Sánchez Belda and Sánchez Trujillano, Reference Sánchez Belda and Sánchez Trujillano1986, Guillaumet and Caja, Reference Guillaumet and Caja2001) although recent studies have reported higher LS averages in genetically improved flocks (1.7 lambs per birth; Casellas et al., Reference Casellas, Caja, Ferret and Piedrafita2007b). The Ripollesa National Breeders Association (Associació Nacional de Criadors d'Ovins de Raça Ripollesa; ANCRI) was founded in year 1987 and focused the selection programme of the Ripollesa breed on litter size (Casellas et al., Reference Casellas, Caja, Ferret and Piedrafita2007b). At this time, the Ripollesa herdbook includes 4 166 purebred ewes in 12 flocks, with a size ranged between 100 and 800 ewes. The current census remains unknown although it is assumed smaller than 50 000 ewes, and with a variable incidence of crossbred individuals (R. Bach, personal communication).
Field data collection and traits analysed
Data were collected from a flock of Ripollesa purebred ewes kept at the experimental farm of the Universitat Autònoma of Barcelona (Bellaterra, Spain) since 1986. This flock was founded from the acquisition of ewes and rams from three purebred Ripollesa farms. Flock size varied between 80 and 120 ewes that lambed once per year and followed an autumn-lambing system, with the exception of replacement ewe-lambs that lambed in December-January since year 1995. See Casellas et al. (Reference Casellas, Caja, Ferret and Piedrafita2007a and Reference Casellas, Caja, Ferret and Piedrafitab) for a detailed description of the management system. Reproductive records were recorded from 1986 to the present. Lambs were ear-tagged at birth and sire, dam, date of birth, birth type (single, twin, triplet or quadruplet) and birth weight were recorded.
After editing, records were available on 1 662 single (55%) and twin (45%) deliveries of 380 different ewes, 312 of them having repeated records. Note that triplet (31) and quadruplet (1) deliveries were exceptional and they were removed from the data set. Moreover, it allows for a straightforward definition of BWV and an easy conversion to absolute birth weight differences (see below). The pedigree for these ewes included a total of 21 sires and 411 dams, with all female and most male (92%) ancestors known for animals born within the analysed flock. Three ewe reproductive traits were considered, BWV, LW and LS. Within-litter birth weight variation was defined for twin births as the s.d. between the birth weights of littermates following Damgaard et al. (Reference Damgaard, Rydhmer, Løvendahl and Grandinson2003). Given the exclusion of triplet and quadruplet deliveries from the analysis, the s.d. values can be easily converted into terms of absolute birth weight differences (BWD) with the formula 
Table 1 Number of observations and means±s.e. for each class of each factor and trait

Models and statistical analysis
A multivariate animal model was used in the joint analysis of BWV, LW and LS, with a linear approach for BWV and LW, and a threshold approach (Wright, Reference Wright1934) for LS. Previous analysis showed that threshold models were preferable for LS in the Ripollesa breed (Casellas et al., Reference Casellas, Caja, Ferret and Piedrafita2007a). The assumed operational models included the additive genetic effect of each ewe (a i), the random permanent environmental effect of the ewe (p i) and three systematic sources of variation as follows:

where BWV ijklm, LW ijklm and LS ijkm were the mth phenotypic record for BWV, LW and LS, respectively, AE j was the age of the ewe at lambing ( < 3, 3 to 5, and >5 years), following the categories assumed by Casellas et al. (Reference Casellas, Caja, Ferret and Piedrafita2007a and Reference Casellas, Caja, Ferret and Piedrafitab), YR k was the year of lambing with 20 levels from 1986 to 2005, and BTS l was the birth type–sex of lambs effect with five categories: (1) single birth and male lamb, (2) single birth and female lamb, (3) twin birth and two male lambs, (4) twin birth and one male and one female lambs, and (5) twin birth and two female lambs. The last term, e ijklm, is the corresponding residual term.
Although data normality is not a mandatory attribute in mixed model equations, it is precisely when normality holds that mixed model equations can be viewed as an approximation to the best predictor (Henderson, Reference Henderson1973; Gianola and Fernando, Reference Gianola and Fernando1986). Within this context, normality of BWV and LW was tested on the modal estimation of their residuals (see the Bayesian approach to the multivariate animal model described below) with the Wilk–Shapiro test (Shapiro and Wilk, Reference Shapiro and Wilk1965) implemented in the Univariate procedure of SAS (v.8.2, Statistical Analysis Systems Institute Inc., Cary, NC). A threshold model was assumed for LS (Wright, Reference Wright1934) and therefore, normality was implicitly assumed on the underlying liability scale.
A multivariate linear–threshold model was implemented following the Bayesian methodologies described by Van Tassell et al. (Reference Van Tassell, Van Vleck and Gregory1998). Litter size is a typical example of a productive trait with discrete phenotypic expression. Historically, difficulties with the statistical analysis of categorical traits have led to implementation of approximate methods with controversial results, negative heritabilities included (Fogarty, Reference Fogarty1995), whereas this problem has a conceptually simple solution within the Bayesian framework (Sorensen et al., Reference Sorensen, Andersen, Gianola and Korsgaard1995; Van Tassell et al., Reference Van Tassell, Van Vleck and Gregory1998). In addition, data sets for the estimations of variance components of ovine reproductive traits often come from flocks under genetic selection on those traits, which was the case with our data set (Casellas et al., Reference Casellas, Caja, Ferret and Piedrafita2007b). Frequentist approaches typically ignore this peculiarity, allowing for biased estimates (Wang et al., Reference Wang, Gianola, Sorensen and Jensen1994). From a Bayesian point of view, all of the information is contained in the joint posterior distribution, and a full Bayesian inference is possible (Wang et al., Reference Wang, Gianola, Sorensen and Jensen1994), although the joint posterior, or any marginal posterior distribution becomes the same with or without selection (Sorensen et al., Reference Sorensen, Wang, Jensen and Gianola1994). Within this context, the vectors of BWV (yBWV) and LW (yLW) phenotypic records sorted by ewe and LS liabilities (uLS; Wright, Reference Wright1934) were assumed to be sampled from the following multivariate normal distribution:
![p \left (\left [{\begin{array}{ccc}\mathbf{y}_{BWV} \\ \mathbf{y}_{LW} \\ \mathbf{u}_{LS} \\ \end{array} }\right ]\vert \mathbf{b},\mathbf{p},\mathbf{a},\mathbf{R}\right )\sim MVN \left (\left [{\begin{array}{ccc}\mathbf{Xb}_{BWV} + \mathbf{Z}_{1}\mathbf{p}_{BWV} + \mathbf{Z}_{2}\mathbf{a}_{BWV} \\ \mathbf{Xb}_{LW} + \mathbf{Z}_{1}\mathbf{p}_{LW} + \mathbf{Z}_{2}\mathbf{a}_{LW} \\ \mathbf{Xb}_{LS} + \mathbf{Z}_{1}\mathbf{p}_{LS} + \mathbf{Z}_{2}\mathbf{a}_{LS} \\ \end{array} }\right ],\mathbf{I}\otimes \mathbf{R}\right )](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920213817933-0756:S1751731107727477:S1751731107727477_eqnU2.gif?pub-status=live)
where, X, Z1 and Z2 were the corresponding incidence matrices of systematic ![(\mathbf{b}\prime = [\mathbf{b}\prime _{BWV}\,\mathbf{b}\prime _{LW}\,\mathbf{b}\prime _{LS}]),](https://static.cambridge.org/binary/version/id/?pub-status=live)
![(\mathbf{ p }\prime = [\mathbf{p}\prime _{BWV}\,\mathbf{p}\prime _{LW}\,\mathbf{p}\prime _{LS}]),](https://static.cambridge.org/binary/version/id/?pub-status=live)
![(\mathbf{a}\prime = [\mathbf{a}\prime _{BWV}\,\mathbf{a}\prime _{LW}\,\mathbf{a}\prime _{LS}])](https://static.cambridge.org/binary/version/id/?pub-status=live)

where I(.) was an indicator function with argument as defined within parentheses and t was the threshold that defined the two categories of response within the liability framework. The indicator function had a value of 1 if the evaluated expression was true and a value of 0 otherwise. Following a standard Bayesian development, multivariate normal priors were assumed for additive genetic and permanent environmental effects:

where A was the numerator relationship matrix, and G and P were the additive genetic and permanent environmental (co)variance matrices, respectively, both with dimensions 3 × 3. Three different genetic groups were defined and founders from the same flock of origin were assigned to the same genetic group. Within this context, the numerator relationship matrix was constructed through procedures described by Westell et al. (Reference Westell, Quaas and Van Vleck1988). Flat priors were assumed for systematic effects, as well as for G, P, and R, with the exception of the LS residual variance, which was fitted to 1 (Sorensen et al., Reference Sorensen, Andersen, Gianola and Korsgaard1995) and the residual variance between BWV and LS, which was assumed null because both traits were defined at different temporal stages. For a given trait i, heritability 









In this study, the multivariate model was solved through the Gibbs sampling technique (Gelfand and Smith, Reference Gelfand and Smith1990), to obtain autocorrelated samples from the joint posterior density and subsequently from the marginal posterior densities of all of the unknowns in the model. It implied an additional step to sample LS liabilities and LW and BWV missing values by data augmentation (Tanner and Wong, Reference Tanner and Wong1987). A unique Gibbs sampler chain was launched with 500,000 points and the first 50 000 were discarded as burn-in. The effective length of the burn-in period and chain size were calculated following Raftery and Lewis (Reference Raftery, Lewis, Bernardo, Berger, Dawid and Smith1992) and Geyer (Reference Geyer1992), respectively (Table 2).
Table 2 Length of the burn-in period and effective chain size for each trait analyzed (heritability (h 2) and permanent environmental coefficient (c 2))

Effect of BWV on stillbirths and postnatal mortality
The frequency of stillbirths and dead lambs in twin births were analysed in five different categories of BWV, (1) >0.32 kg and the lamb being the lighter littermate, (2) >0.32 kg and the lamb being the heavier littermate, (3) >0.09 kg (lighter littermate), (4) >0.09 kg (heavier littermate), and (5) ≤ 0.09 kg (both littermates). Those values were arbitrarily chosen to provide the same number of lambs to each category. This analysis was performed on 1 474 twin lambs and losses were grouped as (1) stillbirths (90 lambs), (2) lambs died during the first 7 days of life (75 lambs), and (3) lambs died after the 1st week of life (51 lambs). Frequencies were compared with a χ2 test with 1 degree of freedom.
Results and discussion
Descriptive statistics
Within-litter birth weight variation showed a skewed distribution with mode 0.19, median 0.26, and a slightly greater mean (Figure 1). Nevertheless, its residuals were normally distributed (P>0.05), with a symmetrical density placed around zero (Figure 1). Normality requirements were also adequately met for LW (P>0.1). Table 1 gives descriptive statistics for the litters included in the genetic analysis (only litters with one or two lambs at birth). Average BWV for twin births was 0.31 ± 0.01 kg, i.e. an absolute difference of 0.22 kg between twin littermates. This value is slightly greater than the one reported in newborn piglets (0.25 kg; Damgaard et al., Reference Damgaard, Rydhmer, Løvendahl and Grandinson2003). The average litter weight was 4.89 ± 0.04 kg, and the difference between single and twin births was between 2 and 2.5 kg, depending on the sex of the progeny (Table 1). Single births were observed in 55% of the litters, with an average litter size at birth of 1.45 ± 0.01 lambs, although this value is slightly underestimated due to the exclusion of 31 triplet and one quadruplet deliveries. These values were within the range reported by El Fadili and Leroy (Reference El Fadili and Leroy2001) in Moroccan sheep breeds, and smaller than the averages provided by Freetly and Leymaster (Reference Freetly and Leymaster2004) in Dorset, Rambouillet, Suffolk, Finnsheep and Romanov ewes.

Figure 1 Observed (a) and residual (b) distributions of within-litter birth weight variation.
Variance components and their ratios
Genetic variance was detected for BWV (Table 3) whereas permanent environmental variance was almost null. The mode of the marginal posterior distribution of heritability for BWV was low (0.061) although the zero value was out of the higher posterior density region at 95% (HPD95). This suggests that genetic improvement of BWV by selective breeding could be feasible in the Ripollesa breed. To our knowledge, this is the first estimate of BWV in sheep, and it confirms previous findings in pigs where BWV was reported as being of low heritability (0.08 to 0.10; Högberg and Rydhmer, Reference Högberg and Rydhmer2000; Damgaard et al., Reference Damgaard, Rydhmer, Løvendahl and Grandinson2003). Genetic selection to homogenise litters at birth may be advantageous for a number of other traits, such as lamb survival (Casellas et al., Reference Casellas, Caja, Such and Piedrafita2007c), growth of lambs, and the homogeneity of littermates at weaning (Wilson and Réale, Reference Wilson and Réale2006).
Table 3 Variance components, correlations, permanent environment coefficients, and heritabilities for the traits analysed

† 




The heritability for LW was 0.200, with an HPD95 that ranged between 0.087 and 0.277. Although the genetic component of LW has not been widely analysed in sheep, our heritability estimate was comparable with those reported by Abdulkhaliq et al. (Reference Abdulkhaliq, Harvey and Parker1989) in Columbia, Suffolk and Targhee breeds, and higher than the heritability observed in Moroccan sheep breeds (El Fadili and Leroy, Reference El Fadili and Leroy2001). Nevertheless, these values were lower than the ones reported in pigs (Sorensen et al., Reference Sorensen, Vernersen and Andersen2000). In a similar way, the mode of the permanent environmental coefficient was 0.199, with its HPD95 ranging between 0.146 and 0.281 (Table 3).
Litter size is one of the most studied reproductive traits in sheep, and a wide range of heritabilities has been published. Our estimate (0.141; Table 3) agrees with the value previously obtained in the same Ripollesa flock (0.131; Casellas et al., Reference Casellas, Caja, Ferret and Piedrafita2007b), although the HPD95 was smaller for the current heritability (0.057 to 0.226). Our heritability estimate was greater than the one observed in Rasa Aragonesa (0.08; Altarriba et al., Reference Altarriba, Varona, García-Cortés and Moreno1998) and the 0.10 reported by Fogarty (Reference Fogarty1995), which was an average of estimates obtained in several sheep breeds. Nevertheless, our estimate was clearly lower than the ones reported in Rambouillet and Finnsheep (0.45 and 0.14; Matos et al., Reference Matos, Thomas, Gianola, Tempelman and Young1997), and in two Norwegian sheep breeds, Dala and Spælsau (0.26 and 0.39; Olesen et al., Reference Olesen, Pérez-Enciso, Gianola and Thomas1994). The permanent environmental coefficient for LS was within the range of previous estimates in Ripollesa sheep (Casellas et al., Reference Casellas, Caja, Ferret and Piedrafita2007b).
Genetic, permanent environmental and residual correlations
The genetic correlations of BWV with LW and LS were moderately positive (0.151) and negative ( − 0.219), respectively. Nevertheless, both HPD95 showed a high degree of uncertainty with the null genetic correlation included within the highest probability range (Table 3), probably due to the relatively small number of twin litters. Although our estimates only suggested potential genetic correlations, it is interesting to note that they were opposite to the ones observed by Damgaard et al. (Reference Damgaard, Rydhmer, Løvendahl and Grandinson2003) in sows and to the negative genetic correlation between BWV and LW reported by Gutiérrez et al. (Reference Gutiérrez, Nieto, Piqueras, Ibáñez and Salgado2006) in mice. As a whole, those results suggested that current selection programmes for LS in the Ripollesa breed (Casellas et al., Reference Casellas, Caja, Ferret and Piedrafita2007b) do not genetically increase lamb birth weight heterogeneity. A negative genetic correlation ( − 0.320) with a HPD95 that ranged between − 0.668 and 0.274 was suggested between LW and LS. That value disagrees with the positive genetic correlation described by El Fadili and Leroy (Reference El Fadili and Leroy2001) in Moroccan sheep breeds.
The permanent environmental correlation between BWV and LW was small and positive (0.187), with a wide HPD95 ranging between − 0.388 and 0.590 (Table 3). It could be related with the small permanent environmental coefficient for BWV. Nevertheless, the permanent environmental effect of LS was negatively correlated with BWV ( − 0.872) and LW ( − 0.449; Table 3), both correlations with a HPD95 ranging far away from the null correlation. Within this context, highly prolific ewes could generate lighter and more homogeneous litters, although the correlation between LS and BWV must be corroborated in future studies.
The residual correlation was null between BWV and LW (Table 3). To our knowledge, no comparable results are available in sheep, whereas BWV and average birth weight showed a significant negative residual correlation in pigs (Damgaard et al., Reference Damgaard, Rydhmer, Løvendahl and Grandinson2003). Litter weight and LS residuals were negatively correlated in the Ripollesa ewe ( − 0.762), with a moderate HPD95 ranging between − 0.875 and − 0.496 (Table 3). The inclusion of birth type as an additional systematic effect in the operational model of LW accounts for the increase due to birth type (Freetly and Leymaster, Reference Freetly and Leymaster2004) and, interestingly, the residual correlation implies an additional negative relationship between LW and LS.
Influences of BWV on lamb survivability
There is general agreement that high BWV results in decreased survival in newborn pigs (Roehe and Kalm, Reference Roehe and Kalm2000; Milligan et al., Reference Milligan, Fraser and Kramer2001), although it has not been studied in lambs. The survivability of 1 424 Ripollesa lambs was studied, showing an average stillbirth incidence of 6.32%. Seventy-five deaths occurred during the 1st week of life (5.62%) and 51 lambs died after the 1st week (4.05%) (Table 4). These percentages were similar to those reported by Binns et al. (Reference Binns, Cox, Rizvi and Green2002) and Casellas et al. (Reference Casellas, Caja, Such and Piedrafita2007c). Frequencies were compared with a χ2 test with 1 degree of freedom. Stillbirths were not influenced by BWV (P>0.05), as was previously reported by Leenhouwers et al. (Reference Leenhouwers, van der Lende and Knol1999) and Damgaard et al. (Reference Damgaard, Rydhmer, Løvendahl and Grandinson2003) in swine. On the other hand, early postnatal mortality varied with BWV (P < 0.05), with an opposed effect on heavier and lighter littermates, and lamb mortality after the 1st week of life did not show significant differences between BWV categories. Extreme values of BWV significantly (P < 0.05) increased (8.68%) and reduced (2.99%) early lamb mortality for lighter and heavier littermates, respectively. The same trend was observed for intermediate BWV (7.04% and 4.48%) although the difference was not significant (P>0.05). To our best knowledge, these are the first results showing a within-litter divergent effect of BWV on lamb survival, a new endeavor to highlight the key influence of foetal nutrition on the postnatal period (Wu et al., Reference Wu, Bazer, Wallace and Spencer2006). It agrees with the previous research of Mellor (Reference Mellor1983) and Ocak et al. (Reference Ocak, Cam and Kuran2005), which related foetal nutrition and growth with newborn lamb survival.
Table 4 Frequencies of stillbirths and died lambs in five different categories of within-litter birth weight variation (BWV)
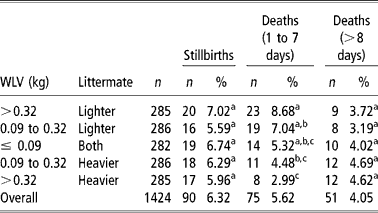
a,b,c Estimates with the same superscript do not differ significantly (P>0.05).
Conclusions
Within-litter birth weight variation in Ripollesa sheep showed a low heritability (0.061), clearly lower than the ones obtained for litter weight (0.200) and litter size (0.141). Nevertheless, genetic selection for birth weight homogeneity seems feasible, and selection by ewes' ability to give homogeneous litters may be advantageous for a number of productive traits, such as lamb survival, as well as for homogenising growth and weaning age in twin births. Within this context, BWV significantly influenced early postnatal lamb mortality, with a divergent effect on heavier and lighter littermates. Within-litter birth weight variation could be genetically correlated with litter weight (0.151) and litter size ( − 0.219), but those estimates suffered from a high degree of uncertainty. This study emphasises the complexity of the genetic architecture of birth weight, a key trait in lamb survival and production.
Acknowledgements
Research supported by a contract with the Departament d'Agricultura, Ramaderia i Pesca de la Generalitat de Catalunya (Spain) and a Universitat Autònoma de Barcelona (Bellaterra, Spain) fellowship granted to J. Casellas. The authors appreciate the assistance of A. Ferret, X. Such, R. Costa and the crew of the S1GCE (Servei de Granges i Camps Experimentals de la UAB, Bellaterra, Spain) for feeding and care of the animals. We thank L. Varona for contributing the software. The English revision of N. Aldam is also acknowledged.







