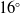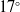Nomenclature
- c
[m]
Aerofoil chord length
-
 ${C_L}$
${C_L}$
[-]
-
Lift coefficient
-
 ${C_P}$
${C_P}$
[-]
-
Pressure coefficient
-
 ${C_{p,rms}}$
${C_{p,rms}}$
[-]
Root-mean-square pressure coefficient
- d
[m]
Aerofoil span
- f
[Hz]
Frequency
- h
[mm]
Nozzle exit height
-
 $l(f)$
$l(f)$
[m]
Spanwise coherence length
- L
[N]
Numerically integrated lift force
- M
[-]
Mach number
- p
[Pa]
Static pressure
- PSD
–
Power spectral density
- RMS
–
Root-mean-square
-
 $R{e_c}$
$R{e_c}$
[-]
Chord-referenced Reynolds number
- St
[-]
Strouhal number
- t
[s]
Time
- u
[ms−1]
Time-averaged velocity
-
 ${U_\infty }$
${U_\infty }$
[ms−1]
Freestream velocity
- w
[mm]
Nozzle exit width
- x
–
Chordwise direction
- y
–
Spanwise direction
- z
–
Direction normal to chord line
-
 $\alpha $
$\alpha $
[°]
Geometric angle of attack
-
 ${\gamma ^2}$
${\gamma ^2}$
[-]
Normalised coherence between unsteady surface pressure fluctuations
-
 $\delta $
$\delta $
[m]
Boundary layer thickness at 99% of freestream velocity
-
 $\xi $
$\xi $
[m]
Microphone separation distance
-
 $\rho $
$\rho $
[kgm−3]
Density of air
-
 ${\tau _c}$
${\tau _c}$
[s]
Temporal correlation scale
-
 ${\phi _{pp}}$
${\phi _{pp}}$
[Pa2/Hz]
Surface pressure fluctuation power spectral density
1.0 Introduction
Aerofoil self-noise is the sound generated by the interaction between an aerofoil and the turbulent structures in its own boundary layer and near-field wake [Reference Brooks, Pope and Marcolini1], and it defines the minimum achievable noise when an aerofoil is embedded in a smooth, non-turbulent flow [Reference Roger and Moreau2, Reference Roger and Moreau3]. The spectral and amplitude characteristics of the resultant sound field are determined by the nature of the turbulent structures, which in turn are determined by the operating condition of the aerofoil and its geometry [Reference Roger and Moreau2]. Brooks et al. [Reference Brooks, Pope and Marcolini1] categorised aerofoil self-noise in subsonic flows into five mechanisms: Turbulent-boundary-layer – trailing-edge noise, laminar-boundary-layer – vortex-shedding noise, separation-stall noise, blunt-trailing-edge – vortex-shedding noise, and tip-vortex formation noise.
The source of aerofoil self-noise is classically regarded to be the scattering of boundary layer turbulent disturbances into acoustic waves as they convect past the geometrical discontinuity of the aerofoil trailing-edge [Reference Roger and Moreau3, Reference Ffowcs Wiliams and Hall4]. Trailing-edge noise, and various methods to reduce it, have been extensively investigated since the advent of aeroacoustic research [Reference Roger and Moreau3, Reference Amiet5–Reference Szoke and Azarpeyvand9]. This is largely due to the dominance of this noise mechanism in most applications when operating in typical conditions [Reference Laratro, Arjomandi, Cazzolato and Kelso10, Reference Mayer, Zang and Azarpeyvand11]. Many models of aerofoil self-noise relate the radiated far-field sound to the near-field hydrodynamics. In the seminal work by Amiet [Reference Amiet5], an analytical model to predict aerofoil trailing-edge noise was developed by formulating the scattered far-field noise using the aerofoil response function and inputs from the incident unsteady pressure spectra and spanwise correlation length of the flow. The model established the significance of the hydrodynamic near-field in the understanding and modelling of the radiated far-field sound.
Aerofoils are not typically operated within the stall regime and, consequently, separation and stall noise has received comparatively less attention than the more frequently encountered laminar- and turbulent-boundary layer induced self-noise mechanisms [Reference Laratro, Arjomandi, Cazzolato and Kelso10]. However, separation and stall noise can still occur in industrially relevant applications since maximum aerodynamic performance is often at high angles-of-attack, near to stall. For instance, when the pressure rise across an axial compressor fan increases to such an extent that the flow reverses and separates, or when a wind turbine blade encounters flow heavily disturbed by an upstream turbine [Reference Bianchi, Corsini, Sheard and Tortora12–Reference Moreau, Roger and Cristophe14]. Additionally, when separation and stall noise does occur, it can be expected to produce higher overall sound levels, particularly at lower frequencies [Reference Moreau, Roger and Cristophe14–Reference Maruta and Kotake16], thereby underlining the importance of developing an understanding of the underlying physics of separation and the near-field hydrodynamics to allow future modelling of the radiated far-field stall noise.
From an aerodynamic perspective, an aerofoil positioned at a high angle-of-attack is in a state of stall when it experiences a sharp fall in its lift, even as the angle-of-attack is further increased, and this stalled state is characterised by the emergence of large-scale separation and mean recirculation over the suction surface of the aerofoil. However, flow separation can occur on an aerofoil without it being stalled; the distinction between separated but not-stalled flow and fully stalled flow is somewhat nebulous and depends on the type of aerofoil and the operating condition. Aerofoil stall can be categorised into one or a combination of the following [Reference McCullough and Gault17, Reference Gault18]: trailing-edge stall where a separation front develops near to the trailing-edge of the aerofoil and moves upstream as the angle-of-attack increases leading to a relatively gradual transition to stall; leading-edge stall where a laminar separation bubble [Reference Arena and Mueller19, Reference Mayle20] near to the leading-edge of the aerofoil abruptly ‘explodes’ and does not reattach downstream causing an abrupt transition to stall; and thin-aerofoil stall where the laminar separation bubble progressively grows as the angle-of-attack increases but does not ‘explode’ leading to a more gradual transition to stall than leading-edge stall.
Much research into separation-stall noise categorises the noise into two regimes: (a) light stall, where, although there is separation, there is still an attached mean flow over part of the aerofoil and noise is radiated primarily from the trailing-edge; and (b) deep stall, where the aerofoil is fully stalled (aerodynamically) with mean recirculation over the aerofoil, and the noise is also radiated from the whole chord in a manner similar to a bluff body [Reference Laratro, Arjomandi, Cazzolato and Kelso10, Reference Moreau, Roger and Cristophe14, Reference Oerlemans21]. As is the case for trailing-edge noise, the flow features in the boundary layer of the aerofoil, and their surface pressure imprint on the aerofoil, are the origin of the radiated far-field noise. Consequently, understanding of the physics of the far-field noise, crucial for the development of any model of this noise, is contingent on understanding of the hydrodynamic near-field [Reference Roger and Moreau3, Reference Roger and Moreau8, Reference Moreau, Roger and Cristophe14, Reference Blake22, Reference Parchen23]. In recent years, high-fidelity near-field hydrodynamic data has been collected for a range of aerofoils, such as various flat plates, symmetric NACA 0012 and NACA 0021 profiles as well as cambered aerofoils such as the NACA 65-(12)10 and NACA 65-410 profiles [Reference Laratro, Arjomandi, Cazzolato and Kelso10, Reference Mayer, Zang and Azarpeyvand11, Reference Moreau, Roger and Cristophe14, Reference Bertagnolio, Madsen, Fischer and Bak24, Reference Lacagnina, Chaitanya, Kim, Berk, Joseph, Choi, Ganapathisubramani, Hasheminejad, Chong, Stalnov, Shahab, Omidyeganeh and Pinelli25]. The near-field hydrodynamic behaviour is strongly dependent on aerofoil shape, and so for the development of generalised far-field noise models, high-fidelity near-field hydrodynamic data for a range of aerofoils is pivotal. For instance, the BPM model [Reference Brooks, Pope and Marcolini1], though widely used in industry [Reference De Gennaro and Kuehnelt26, Reference Oerlemans and Schepers27], is empirically derived from NACA 0012 data and so cannot be expected to provide an accurate model of the radiated far-field noise of aerofoils different in shape to the NACA 0012 profile. Consequently, the collection and dissemination of near-field hydrodynamic data for a wide range of aerofoils is vital for the development of future models of separation and stall noise. This is the context of the present study, where a highly instrumented NACA 16-616 aerofoil has been experimentally investigated in a range of operating conditions as described in the following sections of this paper. The NACA 16-616 aerofoil was selected due to its different shape to the NACA 0012 aerofoil, which was expected to lead to differing stalling behaviour, and due to its industrial relevance to propeller design [Reference Lindsey, Stevenson and Daley28].
The paper is organised as follows: Section 2 summarises the experimental setup and measurement methodology, providing full details on the facilities, test conditions and post-processing techniques used in the present study. Section 3 reports on the static pressure data of the NACA 16-616 aerofoil, revealing the stall behaviour and aerodynamic performance of the aerofoil. Sections 4 to 6 provide a detailed analysis of the surface unsteady pressure fluctuations, providing insights into the nature of the turbulent structures associated with varying angles-of-attack. Subsequently, Section 7 details directly the velocity profiles on the aerofoil suction surface while Section 8 presents far-field sound of the NACA 16-616 aerofoil predicted by Amiet’s model based on the unsteady surface pressure input. Finally, Section 9 summarises the findings of the work, the relevance and applicability of these findings, and the future work that is to be undertaken.
2.0 Experimental setup
The NACA 16-616 experiment was conducted in the aeroacoustic open-jet wind tunnel facility at the University of Bristol. The jet nozzle is located within a chamber that is anechoic for frequencies above 160 Hz. The design and performance of the wind tunnel facility are summarised in Mayer et al. [Reference Mayer, Kamliya Jawahar, Szoke, Showkat Ali and Azarpeyvand29]. For this study, a rectangular nozzle with exit dimensions of height
![]() $h = 775\;{\rm{mm}}$
and width
$h = 775\;{\rm{mm}}$
and width
![]() $w = 500{\rm{\;mm}}$
was employed. Fig. 1(a) provides an overview of the test section mounted within the anechoic facility and flush mounted to the nozzle exit, with a beamforming array positioned above it for far-field noise measurement. Figure 1(b) shows the NACA 16-616 aerofoil installed within the test section and the tensioned Kevlar panels that form the top and bottom walls of the test section. These Kevlar walls are effectively acoustically transparent, allowing acoustic waves to pass through whilst greatly reducing flow deflection in a similar manner to a solid-walled closed test section [Reference Devenport, Burdisso, Borgoltz, Ravetta, Barone, Brown and Morton30]. This minimisation of flow deflection allows for far greater effective angles-of-attack to be achieved than in the classical open-jet configuration, crucially important for the study of stall noise. It has been shown that the geometric aerofoil angle-of-attack can be translated to free-air equivalent effective angles-of-attack [Reference Celik, Mayer and Azarpeyvand31, Reference Corcos32], though for the present study it was found that these corrections were of the order of
$w = 500{\rm{\;mm}}$
was employed. Fig. 1(a) provides an overview of the test section mounted within the anechoic facility and flush mounted to the nozzle exit, with a beamforming array positioned above it for far-field noise measurement. Figure 1(b) shows the NACA 16-616 aerofoil installed within the test section and the tensioned Kevlar panels that form the top and bottom walls of the test section. These Kevlar walls are effectively acoustically transparent, allowing acoustic waves to pass through whilst greatly reducing flow deflection in a similar manner to a solid-walled closed test section [Reference Devenport, Burdisso, Borgoltz, Ravetta, Barone, Brown and Morton30]. This minimisation of flow deflection allows for far greater effective angles-of-attack to be achieved than in the classical open-jet configuration, crucially important for the study of stall noise. It has been shown that the geometric aerofoil angle-of-attack can be translated to free-air equivalent effective angles-of-attack [Reference Celik, Mayer and Azarpeyvand31, Reference Corcos32], though for the present study it was found that these corrections were of the order of
![]() $\sim 0.5{\rm{\% }}$
and so geometric angles-of-attack are presented in this paper. The angle-of-attack of the aerofoil is adjusted manually by rotating the circular end-plates mounted within the sidewalls of the test section. A digital angle gauge was used for measurement of the angle-of-attack. With this arrangement, angle increments of
$\sim 0.5{\rm{\% }}$
and so geometric angles-of-attack are presented in this paper. The angle-of-attack of the aerofoil is adjusted manually by rotating the circular end-plates mounted within the sidewalls of the test section. A digital angle gauge was used for measurement of the angle-of-attack. With this arrangement, angle increments of
![]() $1^\circ $
were tested for angles-of-attack from
$1^\circ $
were tested for angles-of-attack from
![]() $\alpha = - 5^\circ $
to
$\alpha = - 5^\circ $
to
![]() $\alpha = 25^\circ $
.
$\alpha = 25^\circ $
.

Figure 1. Experimental setup: (a) test section mounted to nozzle exit with beamforming array above, and (b) the test section as viewed from a downstream position with the NACA 16-616 aerofoil installed.
A 3D printed aerofoil with a NACA 16-616 profile, a chord length of
![]() $c = 200{\rm{\;mm}}$
, and a span of
$c = 200{\rm{\;mm}}$
, and a span of
![]() $d = 600{\rm{\;mm}}$
, with a wetted span of
$d = 600{\rm{\;mm}}$
, with a wetted span of
![]() $500\;{\rm{mm}}$
, is used in the present study. The aerofoil is tripped on both sides at
$500\;{\rm{mm}}$
, is used in the present study. The aerofoil is tripped on both sides at
![]() $x/c = 0.1$
using
$x/c = 0.1$
using
![]() $6\;{\rm{mm}}$
wide and
$6\;{\rm{mm}}$
wide and
![]() $0.5\;{\rm{mm}}$
thick zigzag turbulator trip tape with a turbulator angle of
$0.5\;{\rm{mm}}$
thick zigzag turbulator trip tape with a turbulator angle of
![]() $70^\circ $
. Static pressure and unsteady surface pressure fluctuations are measured remotely using brass tubes, resin-sealed into the aerofoil surface, with
$70^\circ $
. Static pressure and unsteady surface pressure fluctuations are measured remotely using brass tubes, resin-sealed into the aerofoil surface, with
![]() $0.4\;{\rm{mm}}$
pinholes aligned with the centre-section of the aerofoil span across the chord. Figure 2(a) shows the chordwise distribution of the unsteady surface pressure fluctuation measurement locations, with a high concentration on the aerofoil suction surface. Figure 2(b) shows their spanwise distribution on the suction surface with a spanwise distribution at the aerofoil trailing-edge. Static pressure is measured at 58 locations across the aerofoil chord on both sides and recorded using two synchronised microdaq-32 pressure scanners at a sampling frequency of
$0.4\;{\rm{mm}}$
pinholes aligned with the centre-section of the aerofoil span across the chord. Figure 2(a) shows the chordwise distribution of the unsteady surface pressure fluctuation measurement locations, with a high concentration on the aerofoil suction surface. Figure 2(b) shows their spanwise distribution on the suction surface with a spanwise distribution at the aerofoil trailing-edge. Static pressure is measured at 58 locations across the aerofoil chord on both sides and recorded using two synchronised microdaq-32 pressure scanners at a sampling frequency of
![]() $1{\rm{\;kHz}}$
. The unsteady pressure fluctuations at the 16 locations indicated in Fig. 2 are measured using Panasonic WM-61A microphones, all calibrated in magnitude and phase using a calibrated G.R.A.S. 40PL reference microphone.
$1{\rm{\;kHz}}$
. The unsteady pressure fluctuations at the 16 locations indicated in Fig. 2 are measured using Panasonic WM-61A microphones, all calibrated in magnitude and phase using a calibrated G.R.A.S. 40PL reference microphone.

Figure 2. (a) NACA 16-616 profile with unsteady pressure tap locations, (b) NACA 16-616 planform profile with the spanwise locations, (c) NACA 0012 profile with unsteady pressure tap locations indicated, and (d) NACA 0012 planform profile with the spanwise locations.
All data were recorded with a flow temperature of
![]() $20^\circ {\rm{C}}$
, at a freestream velocity of
$20^\circ {\rm{C}}$
, at a freestream velocity of
![]() $20{\rm{m}}{{\rm{s}}^{ - 1}}$
, corresponding to a chord-referenced Reynolds number of
$20{\rm{m}}{{\rm{s}}^{ - 1}}$
, corresponding to a chord-referenced Reynolds number of
![]() $R{e_c} = 2.7{\rm{x}}{10^5}$
and a Mach number of
$R{e_c} = 2.7{\rm{x}}{10^5}$
and a Mach number of
![]() $M = 0.058$
. Surface pressure fluctuations were recorded at a sampling frequency of
$M = 0.058$
. Surface pressure fluctuations were recorded at a sampling frequency of
![]() ${2^{15}}{\rm{Hz}}$
via a 16 channel National Instruments PXIe-4499 sound and vibration module mounted in a National Instruments PXIe-1062Q chassis. All data were recorded for
${2^{15}}{\rm{Hz}}$
via a 16 channel National Instruments PXIe-4499 sound and vibration module mounted in a National Instruments PXIe-1062Q chassis. All data were recorded for
![]() $32\;{\rm{s}}$
with surface pressure fluctuations and static pressure recorded simultaneously. After collection, all data were processed in the time domain to facilitate calibration, and no further corrections were applied. The power spectral densities of the time-calibrated pressure fluctuation data were calculated using Welch’s method with frequency dependent window sizes of
$32\;{\rm{s}}$
with surface pressure fluctuations and static pressure recorded simultaneously. After collection, all data were processed in the time domain to facilitate calibration, and no further corrections were applied. The power spectral densities of the time-calibrated pressure fluctuation data were calculated using Welch’s method with frequency dependent window sizes of
![]() ${2^{14}},\;{2^{11}},$
and
${2^{14}},\;{2^{11}},$
and
![]() ${2^8}$
samples. A Hanning window with a 50% overlap is used, leading to frequency bin sizes of
${2^8}$
samples. A Hanning window with a 50% overlap is used, leading to frequency bin sizes of
![]() $2\;{\rm{Hz}},{\rm{\;}}16{\rm{\;Hz}},{\rm{\;}}$
and
$2\;{\rm{Hz}},{\rm{\;}}16{\rm{\;Hz}},{\rm{\;}}$
and
![]() $128\;{\rm{Hz}}$
, respectively. The experimental uncertainty of the Panasonic microphones has previously been determined to be
$128\;{\rm{Hz}}$
, respectively. The experimental uncertainty of the Panasonic microphones has previously been determined to be
![]() $ \pm 1.5\;{\rm{dB}}$
with a
$ \pm 1.5\;{\rm{dB}}$
with a
![]() $95\% $
confidence interval [Reference Celik, Mayer and Azarpeyvand31]. The Corcos correction, to account for the finite pin hole size, was not applied to the present data due to the relatively low range of frequencies considered [Reference Corcos32]. The static pressure data, recorded at a sampling frequency of
$95\% $
confidence interval [Reference Celik, Mayer and Azarpeyvand31]. The Corcos correction, to account for the finite pin hole size, was not applied to the present data due to the relatively low range of frequencies considered [Reference Corcos32]. The static pressure data, recorded at a sampling frequency of
![]() $1\;{\rm{kHz}}$
, have a full-scale accuracy of
$1\;{\rm{kHz}}$
, have a full-scale accuracy of
![]() $0.05\% $
and were time averaged and numerically integrated for lift coefficient calculations [Reference Celik, Mayer and Azarpeyvand31].
$0.05\% $
and were time averaged and numerically integrated for lift coefficient calculations [Reference Celik, Mayer and Azarpeyvand31].
Flow velocity measurements were carried out using Constant Temperature Anemometry, with a 55P15 boundary layer hot-wire probe used for boundary layers, and a 55P51 cross-wire probe used for the wake. Both probes were calibrated using a Dantec 54H10 type calibrator and the cross-wire probe was also calibrated for yaw angles between
![]() $ - 40^\circ $
and
$ - 40^\circ $
and
![]() $40^\circ $
. Hot-wire measurements were conducted using a Dantec Streamline Pro system with CTA 91C10 modules, at a sampling frequency of
$40^\circ $
. Hot-wire measurements were conducted using a Dantec Streamline Pro system with CTA 91C10 modules, at a sampling frequency of
![]() ${2^{15}}{\rm{Hz}}$
for
${2^{15}}{\rm{Hz}}$
for
![]() $16\;{\rm{s}}$
, and the measurements were recorded using National Instruments PXIe-4499 modules mounted in a National Instruments PXIe-1062Q chassis. The probes’ movements were controlled using a two-axis ThorLabs LTS300M traverse system [Reference Celik, Bowen and Azarpeyvand33].
$16\;{\rm{s}}$
, and the measurements were recorded using National Instruments PXIe-4499 modules mounted in a National Instruments PXIe-1062Q chassis. The probes’ movements were controlled using a two-axis ThorLabs LTS300M traverse system [Reference Celik, Bowen and Azarpeyvand33].
In Sections 4.0 and 6.0 of this paper, data from the NACA 16-616 aerofoil are compared to those measured from a NACA 0012 aerofoil previously tested in the same anechoic wind tunnel facility, as detailed in Mayer et al. [Reference Mayer, Zang and Azarpeyvand11]. The NACA 0012 aerofoil is hollow in construction with 87 static pressure sensors, the locations of which are shown in Fig. 2(d), and 91 embedded unsteady pressure sensors, of which 21 are operated in a remote sensing configuration, at the locations indicated in Fig. 2(c). The static pressure data are recorded using two synchronised microdaq-32 pressure scanners at a sampling frequency of
![]() $1{\rm{\;kHz}}$
, and the unsteady pressure data are recorded at a sampling rate of
$1{\rm{\;kHz}}$
, and the unsteady pressure data are recorded at a sampling rate of
![]() ${2^{15}}{\rm{Hz}}$
using Knowles FG-23629-P16 condenser microphones for the in-situ sensors and Panasonic WM-61A microphones for the sensors operated in a remote sensing configuration.
${2^{15}}{\rm{Hz}}$
using Knowles FG-23629-P16 condenser microphones for the in-situ sensors and Panasonic WM-61A microphones for the sensors operated in a remote sensing configuration.
3.0 Static pressure results
This section provides an overview of the variation of the mean static pressure distribution over the NACA 16-616 aerofoil surface with the geometric angle-of-attack. Figures 3 and 4 present the static pressure coefficient distribution over the surface of the aerofoil, with the static pressure coefficient defined as:
where p is the surface static pressure,
![]() ${p_\infty }$
is the freestream reference static pressure, and
${p_\infty }$
is the freestream reference static pressure, and
![]() $0.5\rho U_\infty ^2$
is the freestream dynamic pressure.
$0.5\rho U_\infty ^2$
is the freestream dynamic pressure.

Figure 3. (a) Static pressure distribution over the suction surface of a NACA16-616 aerofoil, and (b) the equivalent root-mean-square static pressure distribution.

Figure 4. Static pressure distribution compared to XFoil prediction at (a)
![]() $\alpha = 0^\circ $
, (b)
$\alpha = 0^\circ $
, (b)
![]() $\alpha = 5^\circ $
, (c)
$\alpha = 5^\circ $
, (c)
![]() $\alpha = 10^\circ $
, (d)
$\alpha = 10^\circ $
, (d)
![]() $\alpha = 16^\circ $
, (e)
$\alpha = 16^\circ $
, (e)
![]() $\alpha = 17^\circ $
, and (f)
$\alpha = 17^\circ $
, and (f)
![]() $\alpha = 22^\circ $
angles-of-attack.
$\alpha = 22^\circ $
angles-of-attack.
In Fig. 3(a), the suction surface time-averaged static pressure distribution is shown for all angles-of-attack investigated, from
![]() $ - 5^\circ $
to
$ - 5^\circ $
to
![]() $25^\circ $
, and in Fig. 3(b) the suction surface root-mean-square (RMS) pressure coefficient distribution is presented. With reference to the angle-of-attack, the static pressure distribution shown in Fig. 3(a) can broadly be divided into three regimes: pre-stall for
$25^\circ $
, and in Fig. 3(b) the suction surface root-mean-square (RMS) pressure coefficient distribution is presented. With reference to the angle-of-attack, the static pressure distribution shown in Fig. 3(a) can broadly be divided into three regimes: pre-stall for
![]() $\alpha \le 15^\circ $
, stall for
$\alpha \le 15^\circ $
, stall for
![]() $16^\circ \lt \alpha \le 17^\circ $
, and post-stall for
$16^\circ \lt \alpha \le 17^\circ $
, and post-stall for
![]() $\alpha \ge 18^\circ $
. The stall angle between
$\alpha \ge 18^\circ $
. The stall angle between
![]() $16^\circ $
and
$16^\circ $
and
![]() $17^\circ $
angles-of-attack is more easily discernible from Fig. 4(d) and (e). The pre-stall regime is characterised at the leading-edge by rapid growth of the suction peak, up to a maximum of
$17^\circ $
angles-of-attack is more easily discernible from Fig. 4(d) and (e). The pre-stall regime is characterised at the leading-edge by rapid growth of the suction peak, up to a maximum of
![]() ${C_{p,max}} = - 3.7$
at
${C_{p,max}} = - 3.7$
at
![]() $\alpha = 16^\circ $
. Across the mid-chord, there is a local minimum in the static pressure at
$\alpha = 16^\circ $
. Across the mid-chord, there is a local minimum in the static pressure at
![]() $x/c = 0.6$
for very low angles-of-attack, as is characteristic for the NACA 16-616 profile, and then as the angle-of-attack increases through the pre-stall regime, a strong adverse pressure gradient develops over the whole chord. The stall regime is characterised by abrupt separation of flow at the leading-edge, as indicated by the rapid decrease in the suction peak from
$x/c = 0.6$
for very low angles-of-attack, as is characteristic for the NACA 16-616 profile, and then as the angle-of-attack increases through the pre-stall regime, a strong adverse pressure gradient develops over the whole chord. The stall regime is characterised by abrupt separation of flow at the leading-edge, as indicated by the rapid decrease in the suction peak from
![]() ${C_{p,max}} = - 3.7$
at
${C_{p,max}} = - 3.7$
at
![]() $\alpha = 16^\circ $
to
$\alpha = 16^\circ $
to
![]() ${C_{p,max}} = - 1.5$
at
${C_{p,max}} = - 1.5$
at
![]() $\alpha = 17^\circ $
, and a more gradual decrease in static pressure across the rest of the aerofoil chord as the static pressure distribution transitions to separated flow. The suction surface static pressure distribution post-stall is almost entirely flat, as is characteristic of fully separated flow. The RMS pressure distribution of Fig. 3(b) also shows clearly the three distinct flow regimes, with the pre-stall regime having a flat RMS level almost equal to zero, whilst the stall regime is characterised by a very large peak in RMS levels, particularly at the leading edge with a peak value of
$\alpha = 17^\circ $
, and a more gradual decrease in static pressure across the rest of the aerofoil chord as the static pressure distribution transitions to separated flow. The suction surface static pressure distribution post-stall is almost entirely flat, as is characteristic of fully separated flow. The RMS pressure distribution of Fig. 3(b) also shows clearly the three distinct flow regimes, with the pre-stall regime having a flat RMS level almost equal to zero, whilst the stall regime is characterised by a very large peak in RMS levels, particularly at the leading edge with a peak value of
![]() ${C_{P,rms}} = 0.54$
at
${C_{P,rms}} = 0.54$
at
![]() $x/c = 0$
, and the post-stall regime presents a flat distribution of lower levels than the stall regime but higher than the pre-stall regime. The RMS of the surface pressure is discussed in greater detail later in this section of the paper.
$x/c = 0$
, and the post-stall regime presents a flat distribution of lower levels than the stall regime but higher than the pre-stall regime. The RMS of the surface pressure is discussed in greater detail later in this section of the paper.
Figure 4 shows the full static pressure distribution over the NACA 16-616 aerofoil for six geometric angles-of-attack:
![]() $\alpha = 0^\circ ,{\rm{\;}}5^\circ ,{\rm{\;}}10^\circ ,{\rm{\;}}16^\circ ,{\rm{\;\;}}17^\circ ,$
and
$\alpha = 0^\circ ,{\rm{\;}}5^\circ ,{\rm{\;}}10^\circ ,{\rm{\;}}16^\circ ,{\rm{\;\;}}17^\circ ,$
and
![]() $22^\circ $
. Figure 4(a), (b), and (c) correspond to the pre-stall regime; (d) and (e) correspond to the stall regime; and (f) to the post-stall regime. For the first four cases, the static pressure distribution is compared to XFoil prediction, but it is not for (e) and (f) due to the panel method’s unsuitability for modelling separated flow.
$22^\circ $
. Figure 4(a), (b), and (c) correspond to the pre-stall regime; (d) and (e) correspond to the stall regime; and (f) to the post-stall regime. For the first four cases, the static pressure distribution is compared to XFoil prediction, but it is not for (e) and (f) due to the panel method’s unsuitability for modelling separated flow.
Results in Fig. 4(a) show that at
![]() $0^\circ $
angle-of-attack, the data obtained experimentally compare well with the XFoil predictions. In Fig. 4(b), the static pressure distribution at
$0^\circ $
angle-of-attack, the data obtained experimentally compare well with the XFoil predictions. In Fig. 4(b), the static pressure distribution at
![]() $5^\circ $
angle-of-attack is shown and again compared to XFoil. The two broadly compare well except at the leading-edge where the simulation overpredicts the suction peak. Figure 4(c) and (d), corresponding to
$5^\circ $
angle-of-attack is shown and again compared to XFoil. The two broadly compare well except at the leading-edge where the simulation overpredicts the suction peak. Figure 4(c) and (d), corresponding to
![]() $10^\circ $
and
$10^\circ $
and
![]() $16^\circ $
angles-of-attack, respectively, show the development of a strong suction peak at the aerofoil leading-edge which is evidently not fully captured in the experimental data due to the very small area of the aerofoil over which it occurs not being sufficiently covered by static pressure sensors. In Fig. 4(d), for chordwise positions beyond
$16^\circ $
angles-of-attack, respectively, show the development of a strong suction peak at the aerofoil leading-edge which is evidently not fully captured in the experimental data due to the very small area of the aerofoil over which it occurs not being sufficiently covered by static pressure sensors. In Fig. 4(d), for chordwise positions beyond
![]() $x/c = 0.6$
, the static pressure distribution along the aerofoil suction surface is broadly flat with
$x/c = 0.6$
, the static pressure distribution along the aerofoil suction surface is broadly flat with
![]() ${C_P} = - 0.3$
, suggesting a separated boundary layer. Figure 4(e) shows that the static pressure distribution at
${C_P} = - 0.3$
, suggesting a separated boundary layer. Figure 4(e) shows that the static pressure distribution at
![]() $17^\circ $
angle-of-attack is significantly different to that at
$17^\circ $
angle-of-attack is significantly different to that at
![]() $16^\circ $
, reflecting the abrupt nature of the stall of the NACA 16-616 aerofoil, with the suction surface distribution having a different shape characteristic of very weakly attached flow. Finally, Fig. 4(f) shows the static pressure distribution at
$16^\circ $
, reflecting the abrupt nature of the stall of the NACA 16-616 aerofoil, with the suction surface distribution having a different shape characteristic of very weakly attached flow. Finally, Fig. 4(f) shows the static pressure distribution at
![]() $22^\circ $
angle-of-attack where the aerofoil is fully stalled, and the entirely flat pressure distribution across the chord suggests that the leading-edge separation has occurred upstream of the furthest upstream pressure sensing location on the aerofoil’s leading-edge. This is in contrast to the
$22^\circ $
angle-of-attack where the aerofoil is fully stalled, and the entirely flat pressure distribution across the chord suggests that the leading-edge separation has occurred upstream of the furthest upstream pressure sensing location on the aerofoil’s leading-edge. This is in contrast to the
![]() $17^\circ $
angle-of-attack case where there still exists a mild suction peak, suggesting weakly attached flow at the aerofoil leading-edge.
$17^\circ $
angle-of-attack case where there still exists a mild suction peak, suggesting weakly attached flow at the aerofoil leading-edge.
In assessing the relative accuracy of the experimental data and the XFoil prediction in the pre-stall regime, it should be noted that the XFoil prediction can be expected to capture the suction peak near to the aerofoil’s leading-edge more accurately due to the physical constraints on the experimental model limiting the density of static pressure sensing locations. Conversely, the XFoil prediction does not accurately capture the relatively complex trailing-edge separation mechanism occurring within the pre-stall regime and so nearer to the trailing-edge, the experimental results are more trustworthy.
In addition to the time-averaged static pressure results presented in Figs. 3 and 4, the extent to which the measured static pressure deviates from its mean value can be considered, giving an indication of the nature of the flow in the boundary layers of the aerofoil via their surface pressure imprint. Figure 5(a) shows the RMS of the static pressure distribution on the aerofoil suction surface for three angles-of-attack in the pre-stall regime. The higher RMS levels across the chord as the angle-of-attack increases reflect the increasingly energetic turbulent structures within the growing boundary layer of the NACA 16-616 aerofoil. Of note is the larger increase in the RMS levels for the
![]() $10^\circ $
angle-of-attack case at both the leading-edge and the trailing-edge as compared to the other two angles-of-attack, suggesting that the velocity fluctuations are much more energetic in these areas of the aerofoil chord, and hinting at the likely origin of the aerofoil’s subsequent stall at higher angles-of-attack. Figure 5(b) shows the RMS static pressure coefficient distribution on the aerofoil suction surface in the stall and post-stall regimes. The onset of stall between
$10^\circ $
angle-of-attack case at both the leading-edge and the trailing-edge as compared to the other two angles-of-attack, suggesting that the velocity fluctuations are much more energetic in these areas of the aerofoil chord, and hinting at the likely origin of the aerofoil’s subsequent stall at higher angles-of-attack. Figure 5(b) shows the RMS static pressure coefficient distribution on the aerofoil suction surface in the stall and post-stall regimes. The onset of stall between
![]() $16^\circ $
and
$16^\circ $
and
![]() $17^\circ $
angle-of-attack is strongly indicated by the large-scale increase in RMS levels for the
$17^\circ $
angle-of-attack is strongly indicated by the large-scale increase in RMS levels for the
![]() $17^\circ $
case, with a peak value at the leading-edge of
$17^\circ $
case, with a peak value at the leading-edge of
![]() ${C_{P,rms}} = 0.54$
, as compared to the peak value for the
${C_{P,rms}} = 0.54$
, as compared to the peak value for the
![]() $16^\circ $
case of
$16^\circ $
case of
![]() ${C_{P,rms}} = 0.07$
. Additionally, the presence of the RMS peak at the leading-edge of the aerofoil strongly suggests that the stall of the NACA 16-616 aerofoil is dominated by a leading-edge stall mechanism. For the
${C_{P,rms}} = 0.07$
. Additionally, the presence of the RMS peak at the leading-edge of the aerofoil strongly suggests that the stall of the NACA 16-616 aerofoil is dominated by a leading-edge stall mechanism. For the
![]() $22^\circ $
angle-of-attack case, corresponding to the post-stall regime, the broadly flat RMS distribution across the aerofoil chord indicates low amplitude static pressure fluctuations on the aerofoil surface, suggesting fully separated flow where turbulent structures in the flow are causing reduced unsteady pressure variations on the aerofoil surface. The RMS of the static pressure presented in this section provides a general indication of the nature of the flow near to the aerofoil surface. However, in Section 4.0 the energy-frequency content of the surface pressure fluctuations is considered by studying their power spectral density, providing a higher-fidelity measure of the nature of the flow.
$22^\circ $
angle-of-attack case, corresponding to the post-stall regime, the broadly flat RMS distribution across the aerofoil chord indicates low amplitude static pressure fluctuations on the aerofoil surface, suggesting fully separated flow where turbulent structures in the flow are causing reduced unsteady pressure variations on the aerofoil surface. The RMS of the static pressure presented in this section provides a general indication of the nature of the flow near to the aerofoil surface. However, in Section 4.0 the energy-frequency content of the surface pressure fluctuations is considered by studying their power spectral density, providing a higher-fidelity measure of the nature of the flow.

Figure 5. Root-mean-square suction surface static pressure distribution in the (a) pre-stall regime, and (b) stall and post-stall regimes.
As discussed in Section 1.0, the stalling behaviour of an aerofoil can be characterised by the variation of the lift coefficient, with the angle-of-attack corresponding to the peak
![]() ${C_L}$
defining the stall angle and with the shape of the lift coefficient curve post-stall being associated with the stalling mechanism. The lift coefficient of the aerofoil can be approximated by numerical integration of the static pressure distribution over the aerofoil chord as follows
${C_L}$
defining the stall angle and with the shape of the lift coefficient curve post-stall being associated with the stalling mechanism. The lift coefficient of the aerofoil can be approximated by numerical integration of the static pressure distribution over the aerofoil chord as follows
where L is the numerically integrated lift force, and
![]() ${\rm{c}}$
is the aerofoil chord length.
${\rm{c}}$
is the aerofoil chord length.
Figure 6(a) shows the variation of the static-pressure-derived lift coefficient of the NACA 16-616 aerofoil with angle-of-attack at the freestream velocity of
![]() $U = 20{\rm{m}}{{\rm{s}}^{ - 1}}$
. As seen, the peak lift coefficient of
$U = 20{\rm{m}}{{\rm{s}}^{ - 1}}$
. As seen, the peak lift coefficient of
![]() ${{\rm{C}}_{\rm{L}}} = 0.95$
at
${{\rm{C}}_{\rm{L}}} = 0.95$
at
![]() $\alpha = 16^\circ $
implies that stall occurs between
$\alpha = 16^\circ $
implies that stall occurs between
![]() $\alpha = 16^\circ $
and
$\alpha = 16^\circ $
and
![]() $17^\circ $
, corroborating the suggested stall angle from the static pressure distribution of Fig. 3. Post-stall, the lift coefficient decreases relatively abruptly, reflecting the abrupt change in the static pressure distribution previously discussed. The RMS of the lift coefficient, presented in Fig. 6(b), provides an indication of the unsteady aerodynamic loading on the NACA 16-616 aerofoil throughout the three flow regimes. In the pre-stall regime, for angles-of-attack
$17^\circ $
, corroborating the suggested stall angle from the static pressure distribution of Fig. 3. Post-stall, the lift coefficient decreases relatively abruptly, reflecting the abrupt change in the static pressure distribution previously discussed. The RMS of the lift coefficient, presented in Fig. 6(b), provides an indication of the unsteady aerodynamic loading on the NACA 16-616 aerofoil throughout the three flow regimes. In the pre-stall regime, for angles-of-attack
![]() $\alpha \le 15^\circ $
, the boundary layers on the aerofoil are clearly stable, as indicated by the low level of deviation from the mean lift coefficient. Conversely, in the stall and early post-stall regime, there are significantly higher fluctuations in the lift coefficient, which is likely associated with the onset of unsteady shedding from the separated shear layers as the root of the leading-edge stall mechanism. Therefore, the peak of these fluctuations occurs after the stall angle, as has been previously observed [Reference Sandham34].
$\alpha \le 15^\circ $
, the boundary layers on the aerofoil are clearly stable, as indicated by the low level of deviation from the mean lift coefficient. Conversely, in the stall and early post-stall regime, there are significantly higher fluctuations in the lift coefficient, which is likely associated with the onset of unsteady shedding from the separated shear layers as the root of the leading-edge stall mechanism. Therefore, the peak of these fluctuations occurs after the stall angle, as has been previously observed [Reference Sandham34].

Figure 6. (a) Variation of lift coefficient with angle-of-attack, and (b) variation of RMS lift coefficient with angle-of-attack. Angles-of-attack to be presented subsequently are indicated in red (
![]() $\alpha = 0^\circ ,\;5^\circ ,\;10^\circ ,\;16^\circ ,\;17^\circ $
and
$\alpha = 0^\circ ,\;5^\circ ,\;10^\circ ,\;16^\circ ,\;17^\circ $
and
![]() $22^\circ $
).
$22^\circ $
).
Also indicated in Fig. 6 are the six angles-of-attack presented in the subsequent sections of this paper,
![]() $\alpha = 0^\circ ,\;5^\circ ,\;10^\circ ,\;16^\circ ,\;17^\circ ,{\rm{\;}}$
and
$\alpha = 0^\circ ,\;5^\circ ,\;10^\circ ,\;16^\circ ,\;17^\circ ,{\rm{\;}}$
and
![]() $22^\circ $
, selected to encompass all three flow regimes as previously described: pre-stall, stall and post-stall. Although
$22^\circ $
, selected to encompass all three flow regimes as previously described: pre-stall, stall and post-stall. Although
![]() $16^\circ $
and
$16^\circ $
and
![]() $17^\circ $
angles-of-attack are very close together, they are selected to better understand the advent of stall which is very abrupt in nature and occurs between these angles-of-attack.
$17^\circ $
angles-of-attack are very close together, they are selected to better understand the advent of stall which is very abrupt in nature and occurs between these angles-of-attack.
4.0. Power spectral density of surface pressure fluctuations
This section provides an analysis of the surface pressure fluctuation data recorded for the angles-of-attack
![]() $\alpha = 0^\circ ,{\rm{\;}}5^\circ ,{\rm{\;}}10^\circ ,{\rm{\;}}16^\circ ,{\rm{\;}}17^\circ ,{\rm{\;}}$
and
$\alpha = 0^\circ ,{\rm{\;}}5^\circ ,{\rm{\;}}10^\circ ,{\rm{\;}}16^\circ ,{\rm{\;}}17^\circ ,{\rm{\;}}$
and
![]() $22^\circ $
, as indicated in Fig. 6. As discussed in Section 1.0, surface pressure fluctuations can be considered the origin of far-field sound, with many hydrodynamic models of aerofoil noise relating far-field trailing-edge noise to the power spectral density (PSD) of the surface pressure fluctuations near to the trailing-edge of the aerofoil [Reference Roger and Moreau3, Reference Amiet5, Reference Howe6, Reference Roger and Moreau8, Reference Blake22, Reference Parchen23]. Analysis of surface pressure fluctuations across a broad range of frequencies facilitates the development of a deeper understanding of the nature of the boundary layer flow. Consequently, surface pressure fluctuations are a crucial parameter in the field of aeroacoustics and are therefore presented subsequently. Additionally, at the end of this section the spectra of the NACA 16-616 aerofoil are compared to those of a previously investigated NACA 0012 aerofoil, described in Section 2.0. The purpose of this comparison is to consider the effect of aerofoil camber, shape and thickness on general PSD spectral behaviour, relative to the extensively studied NACA 0012 aerofoil [Reference Brooks, Pope and Marcolini1, Reference Mayer, Kamliya Jawahar, Szoke, Showkat Ali and Azarpeyvand29, Reference Sagrado35].
$22^\circ $
, as indicated in Fig. 6. As discussed in Section 1.0, surface pressure fluctuations can be considered the origin of far-field sound, with many hydrodynamic models of aerofoil noise relating far-field trailing-edge noise to the power spectral density (PSD) of the surface pressure fluctuations near to the trailing-edge of the aerofoil [Reference Roger and Moreau3, Reference Amiet5, Reference Howe6, Reference Roger and Moreau8, Reference Blake22, Reference Parchen23]. Analysis of surface pressure fluctuations across a broad range of frequencies facilitates the development of a deeper understanding of the nature of the boundary layer flow. Consequently, surface pressure fluctuations are a crucial parameter in the field of aeroacoustics and are therefore presented subsequently. Additionally, at the end of this section the spectra of the NACA 16-616 aerofoil are compared to those of a previously investigated NACA 0012 aerofoil, described in Section 2.0. The purpose of this comparison is to consider the effect of aerofoil camber, shape and thickness on general PSD spectral behaviour, relative to the extensively studied NACA 0012 aerofoil [Reference Brooks, Pope and Marcolini1, Reference Mayer, Kamliya Jawahar, Szoke, Showkat Ali and Azarpeyvand29, Reference Sagrado35].
Figure 7 shows the variation of surface pressure fluctuation PSD with angle-of-attack for four chordwise positions on the NACA 16-616 aerofoil suction surface:
![]() $x/c = 0.45,\;0.75,\;0.90,$
and
$x/c = 0.45,\;0.75,\;0.90,$
and
![]() $0.97$
. Note that all surface pressure fluctuation PSDs,
$0.97$
. Note that all surface pressure fluctuation PSDs,
![]() ${\phi _{pp}}$
, are presented logarithmically and are normalised by a reference pressure of
${\phi _{pp}}$
, are presented logarithmically and are normalised by a reference pressure of
![]() ${p_0} = 20\;{\rm{\mu Pa}}$
. In all four surface contours of Fig. 7, the three distinct flow regimes can be identified in the spectra: pre-stall (for
${p_0} = 20\;{\rm{\mu Pa}}$
. In all four surface contours of Fig. 7, the three distinct flow regimes can be identified in the spectra: pre-stall (for
![]() $0^\circ $
to
$0^\circ $
to
![]() $15^\circ $
angles-of-attack), stall (
$15^\circ $
angles-of-attack), stall (
![]() $16^\circ $
and
$16^\circ $
and
![]() $17^\circ $
angles-of-attack) and post-stall (for angles-of-attack beyond
$17^\circ $
angles-of-attack) and post-stall (for angles-of-attack beyond
![]() $17^\circ $
). In the pre-stall regime of the spectra of Fig. 7(a), corresponding to
$17^\circ $
). In the pre-stall regime of the spectra of Fig. 7(a), corresponding to
![]() $x/c = 0.45$
, the surface pressure PSD at this mid-chord location is broadband in nature with no clear peak and a gradual higher frequency roll-off. Spectral levels increase as the angle-of-attack is increased. In the stall regime, there is a very abrupt increase in the PSD across the presented frequency range and particularly at low frequencies, reflecting the sudden emergence of much larger-scale turbulent structures as the aerofoil undergoes stall. In the post-stall regime, there is little variation in spectral shape as the angle-of-attack is increased, except for the development of a peak at a frequency of
$x/c = 0.45$
, the surface pressure PSD at this mid-chord location is broadband in nature with no clear peak and a gradual higher frequency roll-off. Spectral levels increase as the angle-of-attack is increased. In the stall regime, there is a very abrupt increase in the PSD across the presented frequency range and particularly at low frequencies, reflecting the sudden emergence of much larger-scale turbulent structures as the aerofoil undergoes stall. In the post-stall regime, there is little variation in spectral shape as the angle-of-attack is increased, except for the development of a peak at a frequency of
![]() $f = 50{\rm{\;Hz}}$
, corresponding to a frontal-area-referenced Strouhal number of
$f = 50{\rm{\;Hz}}$
, corresponding to a frontal-area-referenced Strouhal number of
![]() $St = 0.2$
, at angles-of-attack beyond
$St = 0.2$
, at angles-of-attack beyond
![]() $22^\circ $
, which has been previously established to be associated with vortex shedding [Reference Moreau, Roger and Cristophe14, Reference Yarusevych, Sullivan and Kawall36]. In the post-stall regime (
$22^\circ $
, which has been previously established to be associated with vortex shedding [Reference Moreau, Roger and Cristophe14, Reference Yarusevych, Sullivan and Kawall36]. In the post-stall regime (
![]() $\alpha \ge 18^\circ $
), the PSD rolls-off at higher frequencies at a rate of
$\alpha \ge 18^\circ $
), the PSD rolls-off at higher frequencies at a rate of
![]() ${f^{ - 2.5}}$
. Figure 7(b) presents the spectra at the further downstream location of
${f^{ - 2.5}}$
. Figure 7(b) presents the spectra at the further downstream location of
![]() $x/c = 0.75$
, and, in the pre-stall regime, the PSD behaviour is broadly similar until
$x/c = 0.75$
, and, in the pre-stall regime, the PSD behaviour is broadly similar until
![]() $12^\circ $
angle-of-attack. However, for angles-of-attack beyond
$12^\circ $
angle-of-attack. However, for angles-of-attack beyond
![]() $12^\circ $
in the pre-stall regime, there is a notable increase in low frequency PSD and a corresponding strong higher frequency roll-off beyond
$12^\circ $
in the pre-stall regime, there is a notable increase in low frequency PSD and a corresponding strong higher frequency roll-off beyond
![]() $f = 1200{\rm{\;Hz}}$
with a spectral decay rate of
$f = 1200{\rm{\;Hz}}$
with a spectral decay rate of
![]() ${f^{ - 2.5}}$
that does not occur at upstream locations, i.e.,
${f^{ - 2.5}}$
that does not occur at upstream locations, i.e.,
![]() $x/c = 0.45$
as seen in Fig. 7(a). This low frequency increase and high frequency roll-off is indicative of significant boundary layer growth with larger, lower frequency, turbulent structures dominating the energy content of the surface pressure fluctuations. The behaviour in the stall regime at
$x/c = 0.45$
as seen in Fig. 7(a). This low frequency increase and high frequency roll-off is indicative of significant boundary layer growth with larger, lower frequency, turbulent structures dominating the energy content of the surface pressure fluctuations. The behaviour in the stall regime at
![]() $x/c = 0.75{\rm{\;}}$
is very similar to that at
$x/c = 0.75{\rm{\;}}$
is very similar to that at
![]() $x/c = 0.45,$
and this is reflective of the abrupt effect stall has on the whole aerofoil chord. Similarly, the post-stall regime behaviour is almost identical between the two cases, reflecting the full-chord separated flow in the post-stall regime.
$x/c = 0.45,$
and this is reflective of the abrupt effect stall has on the whole aerofoil chord. Similarly, the post-stall regime behaviour is almost identical between the two cases, reflecting the full-chord separated flow in the post-stall regime.

Figure 7. Surface pressure fluctuations PSD variation with angle-of-attack at (a)
![]() $x/c = 0.45$
, (b)
$x/c = 0.45$
, (b)
![]() $x/c = 0.75$
, (c)
$x/c = 0.75$
, (c)
![]() $x/c = 0.90$
, and (d)
$x/c = 0.90$
, and (d)
![]() $x/c = 0.97$
.
$x/c = 0.97$
.
Figure 7(c) then shows the spectra near to the trailing-edge at
![]() $x/c = 0.90$
. In the pre-stall regime (
$x/c = 0.90$
. In the pre-stall regime (
![]() $\alpha \le 15^\circ $
), the behaviour is broadly comparable to the
$\alpha \le 15^\circ $
), the behaviour is broadly comparable to the
![]() $x/c = 0.75$
case, except that the low frequency increase and higher frequency roll-off emerges at
$x/c = 0.75$
case, except that the low frequency increase and higher frequency roll-off emerges at
![]() $2^\circ $
angle-of-attack, far sooner than
$2^\circ $
angle-of-attack, far sooner than
![]() $12^\circ $
as for the upstream case. The development of the underlying boundary layer growth, indicated by the increase in the lower frequencies of the PSD, occurring at a much lower angle-of-attack for the downstream position suggests that, as the aerofoil angle-of-attack is increased, the location of the onset of this boundary layer growth moves upstream. This behaviour is reminiscent of a trailing-edge stalling mechanism where a separation front moves upstream from the trailing-edge as the angle-of-attack is increased until the aerofoil is stalled [Reference Gault18]. For the stall and post-stall regimes, the behaviour is near identical to the cases shown in Fig. 7(a) and (b) and is however more indicative of a leading-edge stalling mechanism. Finally, Fig. 7(d) shows the surface pressure fluctuation PSD at
$12^\circ $
as for the upstream case. The development of the underlying boundary layer growth, indicated by the increase in the lower frequencies of the PSD, occurring at a much lower angle-of-attack for the downstream position suggests that, as the aerofoil angle-of-attack is increased, the location of the onset of this boundary layer growth moves upstream. This behaviour is reminiscent of a trailing-edge stalling mechanism where a separation front moves upstream from the trailing-edge as the angle-of-attack is increased until the aerofoil is stalled [Reference Gault18]. For the stall and post-stall regimes, the behaviour is near identical to the cases shown in Fig. 7(a) and (b) and is however more indicative of a leading-edge stalling mechanism. Finally, Fig. 7(d) shows the surface pressure fluctuation PSD at
![]() $x/c = 0.97$
and for this chordwise position, the pre-stall regime behaviour is markedly different. Even for negative angles-of-attack, the high frequency roll-off at a spectral decay rate of
$x/c = 0.97$
and for this chordwise position, the pre-stall regime behaviour is markedly different. Even for negative angles-of-attack, the high frequency roll-off at a spectral decay rate of
![]() ${f^{ - 2.5}}$
is visible, suggesting that even for very low angles-of-attack the boundary layer near to the trailing-edge is dominated by large-scale turbulent structures typical of near-separated and separated flow. As for the other three cases of Fig. 7, the stall regime behaviour is very similar with an abrupt change in PSD at
${f^{ - 2.5}}$
is visible, suggesting that even for very low angles-of-attack the boundary layer near to the trailing-edge is dominated by large-scale turbulent structures typical of near-separated and separated flow. As for the other three cases of Fig. 7, the stall regime behaviour is very similar with an abrupt change in PSD at
![]() $17^\circ $
, again reinforcing the suggestion of a leading-edge stall mechanism where the surface pressure fluctuations across the aerofoil chord are affected at the same time.
$17^\circ $
, again reinforcing the suggestion of a leading-edge stall mechanism where the surface pressure fluctuations across the aerofoil chord are affected at the same time.
With reference to the stalling behaviours described in Section 1.0, it is clear from the unsteady surface pressure spectra of Fig. 7 that there is a strong leading-edge stall occurring between
![]() $16^\circ $
and
$16^\circ $
and
![]() $17^\circ $
angles-of-attack that dominates the PSD of the surface pressure fluctuations at all chordwise positions on the NACA 16-616 aerofoil suction surface. However, the development of locally separated flow, as indicated by the increasing dominance of lower frequencies in the exerted unsteady surface pressure PSD, during the pre-stall regime near to the trailing-edge, and the fact that the point of separation moves upstream as the angle-of-attack is increased, is strongly reminiscent of a trailing-edge stalling mechanism and it is possible that were it not for the occurrence of the dominant leading-edge stalling mechanism, the aerofoil would eventually stall by a trailing-edge mechanism [Reference Gault18].
$17^\circ $
angles-of-attack that dominates the PSD of the surface pressure fluctuations at all chordwise positions on the NACA 16-616 aerofoil suction surface. However, the development of locally separated flow, as indicated by the increasing dominance of lower frequencies in the exerted unsteady surface pressure PSD, during the pre-stall regime near to the trailing-edge, and the fact that the point of separation moves upstream as the angle-of-attack is increased, is strongly reminiscent of a trailing-edge stalling mechanism and it is possible that were it not for the occurrence of the dominant leading-edge stalling mechanism, the aerofoil would eventually stall by a trailing-edge mechanism [Reference Gault18].
To provide a clearer visualisation of the spectra presented in Fig. 7, allowing for easier comparison of levels and decay rates, the unsteady surface pressure PSDs on the NACA 16-616 suction surface for six angles-of-attack, at the same four chordwise positions as in Fig. 7, are presented in Fig. 8. Figure 8(a), (b), and (c) all correspond to the pre-stall regime and show broadly similar spectral behaviour with broadband PSD spectra at most chordwise positions indicating attached boundary layers, with the PSD levels increasing at each angle-of-attack towards the trailing-edge reflecting chordwise boundary layer growth. However, as the angle-of-attack increases from 0° to 10°, the effect of the previously discussed trailing-edge separation mechanism is immediately apparent. For the 0° angle-of-attack case of Fig. 8(a), the PSD indicates that separation has begun to occur at the trailing-edge of the aerofoil as the PSD level at
![]() $x/c = 0.97$
rolls-off sharply beyond
$x/c = 0.97$
rolls-off sharply beyond
![]() $f = 400\;{\rm{Hz}}$
, with a decay rate of
$f = 400\;{\rm{Hz}}$
, with a decay rate of
![]() ${f^{ - 5}}$
. For the 5° angle-of-attack case of Fig. 8(b), the point of onset of this localised separation near to the trailing-edge has clearly moved upstream from the 0° case because the PSD at
${f^{ - 5}}$
. For the 5° angle-of-attack case of Fig. 8(b), the point of onset of this localised separation near to the trailing-edge has clearly moved upstream from the 0° case because the PSD at
![]() $x/c = 0.90$
also rolls-off, though the decay rate of
$x/c = 0.90$
also rolls-off, though the decay rate of
![]() ${f^{ - 3.5}}$
for both chordwise positions is lower than at 0° angle-of-attack. Further reinforcing this suggestion of a trailing-edge separation mechanism is the very close match between the PSD spectra at
${f^{ - 3.5}}$
for both chordwise positions is lower than at 0° angle-of-attack. Further reinforcing this suggestion of a trailing-edge separation mechanism is the very close match between the PSD spectra at
![]() $x/c = 0.90$
and
$x/c = 0.90$
and
![]() $0.97$
for the 10° case of Fig. 8(c) when compared to the 5° case, suggesting that both these chordwise positions are further from the separation point and so “see” the pressure imprint of larger-scale separated flow.
$0.97$
for the 10° case of Fig. 8(c) when compared to the 5° case, suggesting that both these chordwise positions are further from the separation point and so “see” the pressure imprint of larger-scale separated flow.

Figure 8. Surface pressure fluctuations PSD variation with chordwise position at (a)
![]() $\alpha = 0^\circ $
, (b)
$\alpha = 0^\circ $
, (b)
![]() $\alpha = 5^\circ $
, (c)
$\alpha = 5^\circ $
, (c)
![]() $\alpha = 10^\circ $
, (d)
$\alpha = 10^\circ $
, (d)
![]() $\alpha = 16^\circ $
, (e)
$\alpha = 16^\circ $
, (e)
![]() $\alpha = 17^\circ $
and (f)
$\alpha = 17^\circ $
and (f)
![]() $\alpha = 22^\circ $
angles-of-attack.
$\alpha = 22^\circ $
angles-of-attack.
As previously discussed, although the trailing-edge separation mechanism may eventually lead to the stall of the NACA 16-616 aerofoil, it is ultimately subsumed by a dominant leading-edge stall mechanism between 16° and 17° angles-of-attack, and this is reflected in the PSD spectra for these two angles-of-attack shown in Fig. 8(d) and (e). The PSD spectra for the 16° angle-of-attack case are similar to those of the pre-stall regime and reflect the progression of the trailing-edge separation mechanism, with the separation origination point having moved upstream as indicated by the high frequency roll-off at
![]() $x/c = 0.75$
. However, the PSD spectra at 17° angle-of-attack show markedly different behaviour due to the abrupt leading-edge separation having now occurred. For all chordwise positions, low frequency PSD levels are elevated by ∼
$x/c = 0.75$
. However, the PSD spectra at 17° angle-of-attack show markedly different behaviour due to the abrupt leading-edge separation having now occurred. For all chordwise positions, low frequency PSD levels are elevated by ∼
![]() $20{\rm{dB}}/{\rm{Hz}}$
compared to the 16° case and the PSD levels roll-off monotonically at a decay rate of
$20{\rm{dB}}/{\rm{Hz}}$
compared to the 16° case and the PSD levels roll-off monotonically at a decay rate of
![]() ${f^{ - 2.5}}$
. Figure 8(f), corresponding to the post-stall regime 22° case, shows very similar spectral behaviour and PSD levels as compared to the 17° case, reflecting the minimal change in spectral behaviour post-stall.
${f^{ - 2.5}}$
. Figure 8(f), corresponding to the post-stall regime 22° case, shows very similar spectral behaviour and PSD levels as compared to the 17° case, reflecting the minimal change in spectral behaviour post-stall.
To consider the effect of aerofoil shape, camber and thickness on general PSD spectral behaviour, the spectra of the NACA 16-616 aerofoil are compared to those of a NACA 0012 aerofoil. As noted in Section 2.0, the NACA 0012 data was collected in the same anechoic wind tunnel facility in similar operating conditions, and the NACA 0012 aerofoil was found to stall by a leading-edge mechanism at 14° angle-of-attack [Reference Mayer, Kamliya Jawahar, Szoke, Showkat Ali and Azarpeyvand29, Reference Mayer, Zang and Azarpeyvand37]. The two aerofoils are compared at flow-regime equivalent angles-of-attack in Fig. 9: two in the pre-stall regime, one in the stall regime, and one in the post-stall regime. Figure 9(a) corresponds to 0° angle-of-attack, and over the mid-chord there is a clear match between the aerofoils with a similar broad-band spectral shape for both. However, the PSD behaviour at the trailing-edge is different for the two aerofoils, with the PSD at
![]() $x/c = 0.97$
of the NACA 16-616 aerofoil decaying at
$x/c = 0.97$
of the NACA 16-616 aerofoil decaying at
![]() ${f^{ - 5}}$
beyond
${f^{ - 5}}$
beyond
![]() $f = 400\;{\rm{Hz}}$
suggesting mildly separated flow, whereas the PSD at
$f = 400\;{\rm{Hz}}$
suggesting mildly separated flow, whereas the PSD at
![]() $x/c = 0.98$
of the NACA 0012 aerofoil has the broadband spectral shape associated with fully attached flow. Figure 9(b) then compares the PSD spectra of the two aerofoils at 10° angle-of-attack, still within the pre-stall regime for both, and there is again different behaviour between the aerofoils. For the NACA 0012 aerofoil, the PSD spectra are characteristic of large, attached boundary layers for all chordwise positions. Conversely, for the NACA 16-616 aerofoil the previously identified trailing-edge separation mechanism is clearly demonstrated in the PSD spectra at
$x/c = 0.98$
of the NACA 0012 aerofoil has the broadband spectral shape associated with fully attached flow. Figure 9(b) then compares the PSD spectra of the two aerofoils at 10° angle-of-attack, still within the pre-stall regime for both, and there is again different behaviour between the aerofoils. For the NACA 0012 aerofoil, the PSD spectra are characteristic of large, attached boundary layers for all chordwise positions. Conversely, for the NACA 16-616 aerofoil the previously identified trailing-edge separation mechanism is clearly demonstrated in the PSD spectra at
![]() $x/c = 0.90$
and
$x/c = 0.90$
and
![]() $0.97$
.
$0.97$
.

Figure 9. Surface pressure fluctuations PSD of NACA 16-616 and NACA 0012 aerofoils for four chordwise positions: (a) at
![]() $\alpha = 0^\circ $
, (b) at
$\alpha = 0^\circ $
, (b) at
![]() $\alpha = 10^\circ $
, (c) at
$\alpha = 10^\circ $
, (c) at
![]() $\alpha = 16^\circ $
and
$\alpha = 16^\circ $
and
![]() $\alpha = 14^\circ $
, respectively, corresponding to the stall regime, and (d) at
$\alpha = 14^\circ $
, respectively, corresponding to the stall regime, and (d) at
![]() $\alpha = 22^\circ $
and
$\alpha = 22^\circ $
and
![]() $\alpha = 17^\circ $
, respectively, corresponding to the post-stall regime.
$\alpha = 17^\circ $
, respectively, corresponding to the post-stall regime.
The two aerofoils have very distinct near-field hydrodynamic behaviour for both angles-of-attack within the pre-stall regime which strongly implies that the radiated far-field sound will also exhibit different behaviour [Reference Amiet5, Reference Howe6, Reference Roger and Moreau8]. Figure 9(d) shows the PSD of the NACA 16-616 at
![]() $22^\circ $
angle-of-attack, and the PSD of the NACA 0012 aerofoil at
$22^\circ $
angle-of-attack, and the PSD of the NACA 0012 aerofoil at
![]() $17^\circ $
angle-of-attack. A vortex shedding peak at
$17^\circ $
angle-of-attack. A vortex shedding peak at
![]() $f = 44{\rm{\;Hz}}$
, corresponding to a Strouhal number of
$f = 44{\rm{\;Hz}}$
, corresponding to a Strouhal number of
![]() $St = 0.2$
, is prominent in the NACA 0012 PSD, whereas a similar peak is not visible in the NACA 16-616 PSD, although it should be noted that such a peak is visible for higher angles-of-attack as indicated in Fig. 7. Indicated in both PSD plots of Fig. 9(d) are the decay rates and there is a notable difference between the two: the PSD spectra of the NACA 16-616 aerofoil decay at
$St = 0.2$
, is prominent in the NACA 0012 PSD, whereas a similar peak is not visible in the NACA 16-616 PSD, although it should be noted that such a peak is visible for higher angles-of-attack as indicated in Fig. 7. Indicated in both PSD plots of Fig. 9(d) are the decay rates and there is a notable difference between the two: the PSD spectra of the NACA 16-616 aerofoil decay at
![]() ${f^{ - 2.5}}$
whereas the PSD spectra of the NACA 0012 aerofoil decay at a more gradual
${f^{ - 2.5}}$
whereas the PSD spectra of the NACA 0012 aerofoil decay at a more gradual
![]() ${f^{ - 2}}$
, suggesting that higher-frequency turbulent structures make a greater contribution to the pressure fluctuation energy content for the latter aerofoil when fully stalled. Thus, the two aerofoils still behave slightly differently post-stall even if the same leading-edge stall mechanism has occurred for both. This difference in near-field hydrodynamic spectral behaviour can again be expected to cause different far-field noise spectra post-stall [Reference Roger and Moreau2, Reference Amiet5].
${f^{ - 2}}$
, suggesting that higher-frequency turbulent structures make a greater contribution to the pressure fluctuation energy content for the latter aerofoil when fully stalled. Thus, the two aerofoils still behave slightly differently post-stall even if the same leading-edge stall mechanism has occurred for both. This difference in near-field hydrodynamic spectral behaviour can again be expected to cause different far-field noise spectra post-stall [Reference Roger and Moreau2, Reference Amiet5].
5.0 Autocorrelation of surface pressure fluctuations
This section provides an overview of the autocorrelation of the surface pressure fluctuations, derived from the same underlying data as PSDs. The autocorrelation results can provide useful information about the timescales of structures in the boundary layer via their surface pressure imprint on the aerofoil surface. The order of magnitude of the width of the autocorrelation, i.e. the extent of the time-delay over which the autocorrelation coefficient falls to a local minimum, can be regarded as a temporal correlation scale and is representative of the largest scales within the flow field [Reference Sagrado35]. In the following section, a representative temporal correlation scale,
![]() ${\tau _c}$
, is defined as the time-delay beyond which the autocorrelation falls below
${\tau _c}$
, is defined as the time-delay beyond which the autocorrelation falls below
![]() $0.2$
.
$0.2$
.
Figure 10 shows the suction surface distribution of surface pressure autocorrelation for the six angles-of-attack indicated in Fig. 6 of Section 3.0. Figure 10(a) shows the autocorrelation distribution at
![]() $0^\circ $
angle-of-attack, corresponding to the pre-stall regime where the boundary layer remains attached over the aerofoil chord, and this is reflected in the small magnitude of the time scales from the leading-edge to
$0^\circ $
angle-of-attack, corresponding to the pre-stall regime where the boundary layer remains attached over the aerofoil chord, and this is reflected in the small magnitude of the time scales from the leading-edge to
![]() $x/c = 0.85$
with a temporal correlation scale of
$x/c = 0.85$
with a temporal correlation scale of
![]() ${\tau _c} = 3{\rm{x}}{10^{ - 4}}{\rm{s}}$
. However, near to the trailing-edge, for
${\tau _c} = 3{\rm{x}}{10^{ - 4}}{\rm{s}}$
. However, near to the trailing-edge, for
![]() $x/c \gt 0.85$
, there is a notable increase in the temporal correlation scale with
$x/c \gt 0.85$
, there is a notable increase in the temporal correlation scale with
![]() ${\tau _c} = 9{\rm{x}}{10^{ - 4}}{\rm{s}}$
at
${\tau _c} = 9{\rm{x}}{10^{ - 4}}{\rm{s}}$
at
![]() $\;x/c = 0.97$
, suggesting that the boundary layer rapidly grows in the trailing-edge region, which is likely to lead to local separation, as also suggested in the corresponding power spectral density results of Fig. 8(a). This separation will be subsequently shown in Section 7.0. Figure 10(b) shows the autocorrelation distribution at
$\;x/c = 0.97$
, suggesting that the boundary layer rapidly grows in the trailing-edge region, which is likely to lead to local separation, as also suggested in the corresponding power spectral density results of Fig. 8(a). This separation will be subsequently shown in Section 7.0. Figure 10(b) shows the autocorrelation distribution at
![]() $5^\circ $
angle-of-attack and is very similar to the
$5^\circ $
angle-of-attack and is very similar to the
![]() $0^\circ $
case with a slightly higher temporal correlation scale of
$0^\circ $
case with a slightly higher temporal correlation scale of
![]() ${\tau _c} = 5{\rm{x}}{10^{ - 4}}{\rm{s}}$
across the mid-chord reflecting boundary layer growth, and, at the trailing-edge, a temporal correlation scale of
${\tau _c} = 5{\rm{x}}{10^{ - 4}}{\rm{s}}$
across the mid-chord reflecting boundary layer growth, and, at the trailing-edge, a temporal correlation scale of
![]() ${\tau _c} = 1.4{\rm{x}}{10^{ - 3}}{\rm{s}}$
again suggesting boundary layer growth in this region. Figure 10(c) shows the autocorrelation distribution at
${\tau _c} = 1.4{\rm{x}}{10^{ - 3}}{\rm{s}}$
again suggesting boundary layer growth in this region. Figure 10(c) shows the autocorrelation distribution at
![]() $10^\circ $
angle-of-attack and again the overall behaviour is broadly similar to the two lower angle-of-attack cases, except that the flow structures have a much larger temporal correlation scale of
$10^\circ $
angle-of-attack and again the overall behaviour is broadly similar to the two lower angle-of-attack cases, except that the flow structures have a much larger temporal correlation scale of
![]() ${\tau _c} = 3.2{\rm{x}}{10^{ - 3}}{\rm{s}}$
, indicative of the presence of flow separation at the trailing-edge.
${\tau _c} = 3.2{\rm{x}}{10^{ - 3}}{\rm{s}}$
, indicative of the presence of flow separation at the trailing-edge.

Figure 10. Autocorrelation distributions at (a)
![]() $\alpha = 0^\circ $
, (b)
$\alpha = 0^\circ $
, (b)
![]() $\alpha = 5^\circ $
, (c)
$\alpha = 5^\circ $
, (c)
![]() $\alpha = 10^\circ $
, (d)
$\alpha = 10^\circ $
, (d)
![]() $\alpha = 16^\circ $
, (e)
$\alpha = 16^\circ $
, (e)
![]() $\alpha = 17^\circ $
, and (f)
$\alpha = 17^\circ $
, and (f)
![]() $\alpha = 22^\circ $
angles-of-attack.
$\alpha = 22^\circ $
angles-of-attack.
Figure 10(d) shows the autocorrelation distribution at
![]() $16^\circ $
angle-of-attack, corresponding to the stall regime, as previously described in Section 3.0. As can be seen at this angle-of-attack, the autocorrelation distribution is significantly different to the three pre-stall cases shown in Fig. 10(a), (b), and (c), with a much-increased temporal correlation scale across the aerofoil chord reflecting that the flow has separated over much of the aerofoil chord, namely for chordwise positions beyond
$16^\circ $
angle-of-attack, corresponding to the stall regime, as previously described in Section 3.0. As can be seen at this angle-of-attack, the autocorrelation distribution is significantly different to the three pre-stall cases shown in Fig. 10(a), (b), and (c), with a much-increased temporal correlation scale across the aerofoil chord reflecting that the flow has separated over much of the aerofoil chord, namely for chordwise positions beyond
![]() $x/c \gt 0.6$
. Figure 10(e) shows the autocorrelation distribution at
$x/c \gt 0.6$
. Figure 10(e) shows the autocorrelation distribution at
![]() $17^\circ $
angle-of-attack, just after the previously described leading-edge separation mechanism has occurred, and it can be seen that the flow has separated over the whole of the aerofoil chord with a peak temporal correlation scale of
$17^\circ $
angle-of-attack, just after the previously described leading-edge separation mechanism has occurred, and it can be seen that the flow has separated over the whole of the aerofoil chord with a peak temporal correlation scale of
![]() ${\tau _c} = 0.1{\rm{\;s}}$
at the trailing-edge. Finally, Fig. 10(f) shows the autocorrelation distribution at
${\tau _c} = 0.1{\rm{\;s}}$
at the trailing-edge. Finally, Fig. 10(f) shows the autocorrelation distribution at
![]() $22^\circ $
angle-of-attack and reflects the fully stalled behaviour of the aerofoil at this angle-of-attack, with a very large peak temporal correlation scale across the whole aerofoil chord, distinct from the other angles-of-attack in that there is not a very large difference between the leading-edge and the trailing-edge.
$22^\circ $
angle-of-attack and reflects the fully stalled behaviour of the aerofoil at this angle-of-attack, with a very large peak temporal correlation scale across the whole aerofoil chord, distinct from the other angles-of-attack in that there is not a very large difference between the leading-edge and the trailing-edge.
In summary, for the three plots corresponding to the pre-stall regime, namely Fig. 10(a), (b), and (c), the existence of a separation front upstream of the NACA 16-616 aerofoil trailing-edge that grows and moves upstream as the angle-of-attack increases is suggestive of a trailing-edge separation mechanism, as was also suggested by the PSD data presented in Section 4.0. This trailing-edge separation mechanism is then overtaken by the abrupt whole chord separation observed during the stall regime, as shown in Fig. 10(e) and (f).
6.0. Spanwise coherence of surface pressure fluctuations
In addition to the surface pressure fluctuations, another crucial parameter for understanding the structure of the near-field hydrodynamics is the spanwise length scale of the turbulent structures that are convected past the trailing-edge [Reference Amiet5]. To this end, this section examines the spanwise coherence of the surface pressure fluctuations in the suction surface boundary layer at the trailing-edge of the NACA 16-616 aerofoil, at
![]() $x/c = 0.97$
specifically, and uses this coherence to estimate the spanwise coherence length, a measure of the length scale over which turbulent structures are coherent. The normalised coherence function is defined as
$x/c = 0.97$
specifically, and uses this coherence to estimate the spanwise coherence length, a measure of the length scale over which turbulent structures are coherent. The normalised coherence function is defined as
Within the pre-stall regime, i.e. for angles-of-attack
![]() $\alpha \le 15^\circ $
, and particularly within the early pre-stall regime, the turbulent boundary layer structures convecting over the NACA 16-616 aerofoil trailing-edge are very small in spanwise extent. This is reflected in the minimal spanwise coherence for the three separation distances shown in Fig. 11(a) and (b), corresponding to
$\alpha \le 15^\circ $
, and particularly within the early pre-stall regime, the turbulent boundary layer structures convecting over the NACA 16-616 aerofoil trailing-edge are very small in spanwise extent. This is reflected in the minimal spanwise coherence for the three separation distances shown in Fig. 11(a) and (b), corresponding to
![]() $0^\circ $
and
$0^\circ $
and
![]() $10^\circ $
angles-of-attack, respectively, showing that the spanwise length scale of any turbulent structure for these angles-of-attack is smaller than
$10^\circ $
angles-of-attack, respectively, showing that the spanwise length scale of any turbulent structure for these angles-of-attack is smaller than
![]() $\xi /c = 0.125$
. Increasing the angle-of-attack to
$\xi /c = 0.125$
. Increasing the angle-of-attack to
![]() $10^\circ $
, still within the pre-stall regime, causes an increase in spanwise extent, as shown in Fig. 11(c) where coherence is elevated for the smaller separation distance of
$10^\circ $
, still within the pre-stall regime, causes an increase in spanwise extent, as shown in Fig. 11(c) where coherence is elevated for the smaller separation distance of
![]() $\xi /c = 0.125$
. Moving into the stall regime, i.e. for angles-of-attack
$\xi /c = 0.125$
. Moving into the stall regime, i.e. for angles-of-attack
![]() $16^\circ \lt \alpha \le 17^\circ $
, much larger spanwise structures are clearly present as indicated by the significantly increased coherence levels for each of the three separation distances compared to the pre-stall regime. For instance, peak coherence for the smallest separation distance of
$16^\circ \lt \alpha \le 17^\circ $
, much larger spanwise structures are clearly present as indicated by the significantly increased coherence levels for each of the three separation distances compared to the pre-stall regime. For instance, peak coherence for the smallest separation distance of
![]() $\xi /c = 0.125$
has increased from
$\xi /c = 0.125$
has increased from
![]() ${\gamma ^2} = 0.19$
at
${\gamma ^2} = 0.19$
at
![]() $f = 128{\rm{\;Hz}}$
for the
$f = 128{\rm{\;Hz}}$
for the
![]() $10^\circ $
case of Fig. 11(c) to
$10^\circ $
case of Fig. 11(c) to
![]() ${\gamma ^2} = 0.32$
at
${\gamma ^2} = 0.32$
at
![]() $f = 90{\rm{\;Hz}}$
for the
$f = 90{\rm{\;Hz}}$
for the
![]() $16^\circ $
case of Fig. 11(d). In addition to the generally increased coherence levels in the stall regime, the abrupt effect of the leading-edge separation mechanism that occurs between
$16^\circ $
case of Fig. 11(d). In addition to the generally increased coherence levels in the stall regime, the abrupt effect of the leading-edge separation mechanism that occurs between
![]() $16^\circ $
and
$16^\circ $
and
![]() $17^\circ $
angles-of-attack is readily apparent in Fig. 11(d) and (e). Not only are the coherence levels higher for the
$17^\circ $
angles-of-attack is readily apparent in Fig. 11(d) and (e). Not only are the coherence levels higher for the
![]() $17^\circ $
angle-of-attack case due to the presence of large-scale eddies associated with the leading-edge separation, but there is also a complete shift in spectral behaviour with more clearly defined and lower frequency peaks for each separation distance. This wholesale change in spectral behaviour reflects the wholesale change in boundary layer structure on the suction surface after the leading-edge separation mechanism. Finally, it can be observed that the surface pressure at the trailing-edge is dominated by vortex shedding when the aerofoil is deeply stalled, as shown in Fig. 11(f) where the coherence spectra for each separation distance are dominated by distinct peaks at a frequency of
$17^\circ $
angle-of-attack case due to the presence of large-scale eddies associated with the leading-edge separation, but there is also a complete shift in spectral behaviour with more clearly defined and lower frequency peaks for each separation distance. This wholesale change in spectral behaviour reflects the wholesale change in boundary layer structure on the suction surface after the leading-edge separation mechanism. Finally, it can be observed that the surface pressure at the trailing-edge is dominated by vortex shedding when the aerofoil is deeply stalled, as shown in Fig. 11(f) where the coherence spectra for each separation distance are dominated by distinct peaks at a frequency of
![]() $f = 48\;{\rm{Hz}}$
which corresponds to a Strouhal number of
$f = 48\;{\rm{Hz}}$
which corresponds to a Strouhal number of
![]() $St = 0.2$
, previously established to be associated with vortex shedding [Reference Moreau, Roger and Cristophe14, Reference Yarusevych, Sullivan and Kawall36].
$St = 0.2$
, previously established to be associated with vortex shedding [Reference Moreau, Roger and Cristophe14, Reference Yarusevych, Sullivan and Kawall36].

Figure 11. Spanwise coherence variation with separation distance at
![]() $x/c = 0.97$
, at (a)
$x/c = 0.97$
, at (a)
![]() $\alpha = 0^\circ $
, (b)
$\alpha = 0^\circ $
, (b)
![]() $\alpha = 5^\circ $
, (c)
$\alpha = 5^\circ $
, (c)
![]() $\alpha = 10^\circ $
, (d)
$\alpha = 10^\circ $
, (d)
![]() $\alpha = 16^\circ $
, (e)
$\alpha = 16^\circ $
, (e)
![]() $\alpha = 17^\circ $
, and (f)
$\alpha = 17^\circ $
, and (f)
![]() $\alpha = 22^\circ $
angles-of-attack.
$\alpha = 22^\circ $
angles-of-attack.
The spanwise coherence distributions of Fig. 11 again reinforce the suggestion of a secondary trailing-edge separation mechanism, characterised by a rapidly growing boundary layer near to the NACA 16-616 aerofoil suction surface trailing-edge up to
![]() $16^\circ $
angle-of-attack, that is then subsumed by a dominant leading-edge stalling mechanism between
$16^\circ $
angle-of-attack, that is then subsumed by a dominant leading-edge stalling mechanism between
![]() $16^\circ $
and
$16^\circ $
and
![]() $17^\circ $
angles-of-attack characterised by whole chord suction surface separation. The trailing-edge separation mechanism is suggested by the growing spanwise coherence as the angle-of-attack is increased in the pre-stall regime which reflects the existence of rapidly growing turbulent structures due to boundary layer separation, and the leading-edge stalling mechanism is strongly suggested by the wholesale change in spanwise coherence within the stall regime between
$17^\circ $
angles-of-attack characterised by whole chord suction surface separation. The trailing-edge separation mechanism is suggested by the growing spanwise coherence as the angle-of-attack is increased in the pre-stall regime which reflects the existence of rapidly growing turbulent structures due to boundary layer separation, and the leading-edge stalling mechanism is strongly suggested by the wholesale change in spanwise coherence within the stall regime between
![]() $16^\circ $
and
$16^\circ $
and
![]() $17^\circ $
angles-of-attack.
$17^\circ $
angles-of-attack.
The mean spanwise coherences of the surface pressure fluctuations, shown in Fig. 11, can be used to calculate the spanwise coherence length as a function of frequency,
![]() $l\left( f \right)/c$
, and this is presented for six angles-of-attack in Fig. 12. The method proposed by Palumbo was used [Reference Palumbo38], where an exponential curve is fitted to the graph of coherence against microphone separation distance for each frequency bin, and the coherence length is then the inverse of the exponent of this fitted curve, as shown in Equation 3:
$l\left( f \right)/c$
, and this is presented for six angles-of-attack in Fig. 12. The method proposed by Palumbo was used [Reference Palumbo38], where an exponential curve is fitted to the graph of coherence against microphone separation distance for each frequency bin, and the coherence length is then the inverse of the exponent of this fitted curve, as shown in Equation 3:
Figure 12(a) shows the spanwise coherence length for
![]() $0^\circ $
,
$0^\circ $
,
![]() $5^\circ $
, and
$5^\circ $
, and
![]() $10^\circ $
angles-of-attack, all corresponding to the pre-stall regime previously defined in Section 3.0, and the positive correlation between coherence length and angle-of-attack is evident, reflecting the growth in scale of turbulent structures as the angle-of-attack increases and the boundary layer grows in the pre-stall regime. Figure 12(b) shows the coherence length for the three stall and post-stall regime angles-of-attack, namely
$10^\circ $
angles-of-attack, all corresponding to the pre-stall regime previously defined in Section 3.0, and the positive correlation between coherence length and angle-of-attack is evident, reflecting the growth in scale of turbulent structures as the angle-of-attack increases and the boundary layer grows in the pre-stall regime. Figure 12(b) shows the coherence length for the three stall and post-stall regime angles-of-attack, namely
![]() $16^\circ $
,
$16^\circ $
,
![]() $17^\circ $
and
$17^\circ $
and
![]() $22^\circ $
. For the
$22^\circ $
. For the
![]() $16^\circ $
angle-of-attack case, the spectral shape of the coherence length is very similar to the
$16^\circ $
angle-of-attack case, the spectral shape of the coherence length is very similar to the
![]() $10^\circ $
case of Fig. 12(a) with a peak of
$10^\circ $
case of Fig. 12(a) with a peak of
![]() $l\left( f \right)/c = 0.21$
at a frequency of
$l\left( f \right)/c = 0.21$
at a frequency of
![]() $f = 92{\rm{\;Hz}}$
compared to a smaller peak of
$f = 92{\rm{\;Hz}}$
compared to a smaller peak of
![]() $l\left( f \right)/c = 0.07$
at a frequency of
$l\left( f \right)/c = 0.07$
at a frequency of
![]() $f = 126{\rm{\;Hz}}$
for the pre-stall case. This reflects that the overall boundary layer behaviour at these two angles-of-attack is similar except for the further development of the secondary trailing-edge separation mechanism for the
$f = 126{\rm{\;Hz}}$
for the pre-stall case. This reflects that the overall boundary layer behaviour at these two angles-of-attack is similar except for the further development of the secondary trailing-edge separation mechanism for the
![]() $16^\circ $
angle-of-attack case, as was also evident in the PSD and autocorrelation results of Sections 4.0 and 5.0. Conversely, the
$16^\circ $
angle-of-attack case, as was also evident in the PSD and autocorrelation results of Sections 4.0 and 5.0. Conversely, the
![]() $17^\circ $
and
$17^\circ $
and
![]() $22^\circ $
angles-of-attack cases show a very different spectral shape with a very clear peak coherence length, reflecting that these angles-of-attack are after the dominant leading-edge stall mechanism has occurred, with the peak coherence length for both angles-of-attack occurring at the previously noted vortex shedding frequency of
$22^\circ $
angles-of-attack cases show a very different spectral shape with a very clear peak coherence length, reflecting that these angles-of-attack are after the dominant leading-edge stall mechanism has occurred, with the peak coherence length for both angles-of-attack occurring at the previously noted vortex shedding frequency of
![]() $f = 50{\rm{\;Hz}}$
, with the sharper peak for the
$f = 50{\rm{\;Hz}}$
, with the sharper peak for the
![]() $22^\circ $
case demonstrating the increasing dominance of large, low-frequency eddies at this fully stalled angle-of-attack.
$22^\circ $
case demonstrating the increasing dominance of large, low-frequency eddies at this fully stalled angle-of-attack.

Figure 12. Spanwise coherence length variation with angle-of-attack: (a) pre-stall, and (b) post-stall.
In Fig. 13, the spanwise coherence length results for the NACA 16-616 aerofoil are compared to the NACA 0012 aerofoil previously described in Sections 2.0 and 4.0. As for the unsteady surface pressure PSD results, this comparison is made to develop an understanding of the effect of aerofoil shape and stalling behaviour on the spanwise coherence length and, by extension, their possible effect on the radiated far-field sound. As previously noted, the NACA 0012 data was collected in the same anechoic wind tunnel facility as the present study at similar operating conditions [Reference Mayer, Zang and Azarpeyvand11], and the presented angles-of-attack are flow-regime equivalent to those of the NACA 16-616. The behaviour in the pre-stall regime, at
![]() $0^\circ $
and
$0^\circ $
and
![]() $10^\circ $
angles-of-attack for both aerofoils, is very similar between the two, with a coherence length of less than
$10^\circ $
angles-of-attack for both aerofoils, is very similar between the two, with a coherence length of less than
![]() $0.1c$
, suggesting that large-scale turbulent structures are likely absent in the turbulent boundary layer and that the spanwise length scales are evenly distributed across frequencies lower than 500 Hz, without any spectral peaks. Conversely, the behaviour in the stall regime,
$0.1c$
, suggesting that large-scale turbulent structures are likely absent in the turbulent boundary layer and that the spanwise length scales are evenly distributed across frequencies lower than 500 Hz, without any spectral peaks. Conversely, the behaviour in the stall regime,
![]() $16^\circ $
angle-of-attack for the NACA 16-616 aerofoil and
$16^\circ $
angle-of-attack for the NACA 16-616 aerofoil and
![]() $14^\circ $
angle-of-attack for the NACA 0012 aerofoil, is notably different with the NACA 0012 coherence length showing a strong peak at a frequency of
$14^\circ $
angle-of-attack for the NACA 0012 aerofoil, is notably different with the NACA 0012 coherence length showing a strong peak at a frequency of
![]() $f = 40\;{\rm{Hz}}$
corresponding to vortex shedding [Reference Yarusevych, Sullivan and Kawall36], whereas the NACA 16-616 data shows a broader spectral peak at a higher frequency, associated with large-scale separated flow. For the post-stall regime angles-of-attack,
$f = 40\;{\rm{Hz}}$
corresponding to vortex shedding [Reference Yarusevych, Sullivan and Kawall36], whereas the NACA 16-616 data shows a broader spectral peak at a higher frequency, associated with large-scale separated flow. For the post-stall regime angles-of-attack,
![]() $22^\circ $
for the NACA 16-616 and
$22^\circ $
for the NACA 16-616 and
![]() $17^\circ $
for the NACA 0012, the spectral behaviour is again similar with a clear spectral peak in both corresponding to vortex shedding at frequencies corresponding to a Strouhal number of 0.2. However, comparing the two aerofoils, the NACA 16-616 aerofoil has significantly smaller spanwise length scales than those of the NACA 0012 aerofoil. For instance, the ratios of the spanwise length scales of the NACA 16-616 aerofoil over the NACA 0012 aerofoil are approximately
$17^\circ $
for the NACA 0012, the spectral behaviour is again similar with a clear spectral peak in both corresponding to vortex shedding at frequencies corresponding to a Strouhal number of 0.2. However, comparing the two aerofoils, the NACA 16-616 aerofoil has significantly smaller spanwise length scales than those of the NACA 0012 aerofoil. For instance, the ratios of the spanwise length scales of the NACA 16-616 aerofoil over the NACA 0012 aerofoil are approximately
![]() $0.5$
at the onset of the stall and
$0.5$
at the onset of the stall and
![]() $0.6$
at post-stall. This is indicative of the existence of different flow structures near to the trailing-edges of each aerofoil and, as with the PSDs in Section 4.0, the largest difference between the NACA 16-616 and NACA 0012 aerofoils occurs in the stall regime, which will have significant implications for the radiated far field sound due to its dependence on the hydrodynamic near-field [Reference Amiet5].
$0.6$
at post-stall. This is indicative of the existence of different flow structures near to the trailing-edges of each aerofoil and, as with the PSDs in Section 4.0, the largest difference between the NACA 16-616 and NACA 0012 aerofoils occurs in the stall regime, which will have significant implications for the radiated far field sound due to its dependence on the hydrodynamic near-field [Reference Amiet5].

Figure 13. Spanwise coherence length variation with angle-of-attack: (a) NACA 16-616, and (b) NACA 0012.
7.0 Boundary layer velocity results
In this section, hot-wire anemometry results recorded for the NACA 16-616 aerofoil are examined at five angles-of-attack:
![]() $\alpha = 0^\circ ,{\rm{\;}}5^\circ ,{\rm{\;}}10^\circ ,{\rm{\;}}16^\circ ,{\rm{\;}}17^\circ $
and
$\alpha = 0^\circ ,{\rm{\;}}5^\circ ,{\rm{\;}}10^\circ ,{\rm{\;}}16^\circ ,{\rm{\;}}17^\circ $
and
![]() $22^\circ $
. The results are presented in the form of aerofoil suction surface wake traversals and suction surface boundary layer profiles, providing a direct indication of the nature of the flow within the boundary layer and in particular, whether it is attached, mildly separated or fully separated.
$22^\circ $
. The results are presented in the form of aerofoil suction surface wake traversals and suction surface boundary layer profiles, providing a direct indication of the nature of the flow within the boundary layer and in particular, whether it is attached, mildly separated or fully separated.
Figure 14 presents wake traversal vector fields for four angles-of-attack:
![]() $\alpha = 10^\circ ,{\rm{\;}}16^\circ ,{\rm{\;}}17^\circ $
, and
$\alpha = 10^\circ ,{\rm{\;}}16^\circ ,{\rm{\;}}17^\circ $
, and
![]() $22^\circ $
, with the length of the arrows proportional to the velocity magnitude and the direction reflecting the velocity direction. Figure 14(a) shows the wake traversal for the
$22^\circ $
, with the length of the arrows proportional to the velocity magnitude and the direction reflecting the velocity direction. Figure 14(a) shows the wake traversal for the
![]() $10^\circ $
angle-of-attack case, corresponding to the pre-stall regime, and even for this angle-of-attack small-scale separation at the aerofoil trailing-edge is indicated by the relatively large velocity deficit region aft of the trailing-edge. Figure 14(b) shows the velocity vector field for the
$10^\circ $
angle-of-attack case, corresponding to the pre-stall regime, and even for this angle-of-attack small-scale separation at the aerofoil trailing-edge is indicated by the relatively large velocity deficit region aft of the trailing-edge. Figure 14(b) shows the velocity vector field for the
![]() $16^\circ $
stall regime angle-of-attack case, and again the presence of localised separation in the near-trailing-edge region is indicated by the large velocity deficit at these chordwise locations, whereas for the further upstream locations the boundary layer is still clearly attached to the aerofoil surface. The velocity vector fields of Fig. 14(a) and (b) strongly reinforce the previously suggested secondary trailing-edge separation mechanism with localised separation occurring near to the aerofoil trailing-edge. Figure 14(c) shows the velocity vector field for the
$16^\circ $
stall regime angle-of-attack case, and again the presence of localised separation in the near-trailing-edge region is indicated by the large velocity deficit at these chordwise locations, whereas for the further upstream locations the boundary layer is still clearly attached to the aerofoil surface. The velocity vector fields of Fig. 14(a) and (b) strongly reinforce the previously suggested secondary trailing-edge separation mechanism with localised separation occurring near to the aerofoil trailing-edge. Figure 14(c) shows the velocity vector field for the
![]() $17^\circ $
angle-of-attack case, and the stark difference compared to the
$17^\circ $
angle-of-attack case, and the stark difference compared to the
![]() $16^\circ $
case, with the flow now clearly separated at all chordwise locations, is reflective of the abrupt leading-edge stall that has occurred between these angles-of-attack. For all chordwise positions probed, the flow has clearly separated although the size of this separation region increases towards the trailing-edge of the aerofoil. Finally, Fig. 14(d) shows the velocity vector field for the
$16^\circ $
case, with the flow now clearly separated at all chordwise locations, is reflective of the abrupt leading-edge stall that has occurred between these angles-of-attack. For all chordwise positions probed, the flow has clearly separated although the size of this separation region increases towards the trailing-edge of the aerofoil. Finally, Fig. 14(d) shows the velocity vector field for the
![]() $22^\circ $
angle-of-attack case, and the fully stalled nature of the aerofoil at this angle-of-attack is indicated by the existence of the very large recirculation region near to the trailing-edge.
$22^\circ $
angle-of-attack case, and the fully stalled nature of the aerofoil at this angle-of-attack is indicated by the existence of the very large recirculation region near to the trailing-edge.

Figure 14. Flow velocity vector field at: (a)
![]() $\alpha = 10^\circ $
, (b)
$\alpha = 10^\circ $
, (b)
![]() $\alpha = 16^\circ $
, (c)
$\alpha = 16^\circ $
, (c)
![]() $\alpha = 17^\circ $
and (d)
$\alpha = 17^\circ $
and (d)
![]() $\alpha = 22^\circ $
angles-of-attack.
$\alpha = 22^\circ $
angles-of-attack.
Figure 15 shows the suction surface boundary layer velocity profiles at two chordwise positions for six angles-of-attack, namely
![]() $\alpha = 0^\circ ,5^\circ ,10^\circ ,{\rm{\;}}16^\circ ,{\rm{\;}}17^\circ $
and
$\alpha = 0^\circ ,5^\circ ,10^\circ ,{\rm{\;}}16^\circ ,{\rm{\;}}17^\circ $
and
![]() $22^\circ $
. Figure 15(a) shows the boundary layer profiles for the
$22^\circ $
. Figure 15(a) shows the boundary layer profiles for the
![]() $0^\circ $
angle-of-attack case. For the mid-chord location of
$0^\circ $
angle-of-attack case. For the mid-chord location of
![]() $x/c = 0.6$
, the boundary layer is clearly attached with a 99% boundary layer thickness of
$x/c = 0.6$
, the boundary layer is clearly attached with a 99% boundary layer thickness of
![]() $\delta = 0.012c$
. The boundary layer at the trailing-edge location of
$\delta = 0.012c$
. The boundary layer at the trailing-edge location of
![]() $x/c = 0.98$
however is much larger, and the inflectional point near to the wall suggests that the boundary layer shows signs of separation, with a thickness of
$x/c = 0.98$
however is much larger, and the inflectional point near to the wall suggests that the boundary layer shows signs of separation, with a thickness of
![]() $\delta = 0.055c$
. Figure 15(b) shows the boundary layer profiles at the same chordwise positions but at
$\delta = 0.055c$
. Figure 15(b) shows the boundary layer profiles at the same chordwise positions but at
![]() $5^\circ $
angle-of-attack, and again the boundary layer is still clearly attached on the aerofoil mid-chord with a thickness of
$5^\circ $
angle-of-attack, and again the boundary layer is still clearly attached on the aerofoil mid-chord with a thickness of
![]() $\delta = 0.021c$
. However, for the trailing-edge location of
$\delta = 0.021c$
. However, for the trailing-edge location of
![]() $x/c = 0.98$
, the clear inflection point in the boundary layer profile indicates reversed flow and hence suggests strongly that separation has occurred, corroborating the findings in the unsteady surface pressure fluctuations, and further reinforcing the suggestion of a trailing-edge separation at relatively low angles-of-attack for NACA 16-616. As the angle-of-attack is increased to
$x/c = 0.98$
, the clear inflection point in the boundary layer profile indicates reversed flow and hence suggests strongly that separation has occurred, corroborating the findings in the unsteady surface pressure fluctuations, and further reinforcing the suggestion of a trailing-edge separation at relatively low angles-of-attack for NACA 16-616. As the angle-of-attack is increased to
![]() $10^\circ $
as shown in Fig. 15(c), the boundary layers are very similar to those of the
$10^\circ $
as shown in Fig. 15(c), the boundary layers are very similar to those of the
![]() $5^\circ $
case although they have grown due to the increased adverse pressure gradient. Figure 15(d) shows the velocity profiles at
$5^\circ $
case although they have grown due to the increased adverse pressure gradient. Figure 15(d) shows the velocity profiles at
![]() $16^\circ $
angle-of-attack and similar behaviour can be observed with weakly attached flow at the mid-chord location and separated flow at the trailing-edge.
$16^\circ $
angle-of-attack and similar behaviour can be observed with weakly attached flow at the mid-chord location and separated flow at the trailing-edge.

Figure 15. Boundary layer velocity profiles at angles-of-attack of (a)
![]() $\alpha = 0^\circ $
, (b)
$\alpha = 0^\circ $
, (b)
![]() $\alpha = 5^\circ $
, (c)
$\alpha = 5^\circ $
, (c)
![]() $\alpha = 10^\circ $
, (d)
$\alpha = 10^\circ $
, (d)
![]() $\alpha = 16^\circ $
, (e)
$\alpha = 16^\circ $
, (e)
![]() $\alpha = 17^\circ $
and (f)
$\alpha = 17^\circ $
and (f)
![]() $\alpha = 22^\circ $
.
$\alpha = 22^\circ $
.
Moving further into the stall regime, the abrupt and dominant nature of the previously identified leading-edge separation mechanism is evident when comparing the
![]() $16^\circ $
case of Fig. 15(d) to the
$16^\circ $
case of Fig. 15(d) to the
![]() $17^\circ $
case of Fig. 15(e). At the latter angle-of-attack, the boundary layer profiles at both chordwise locations clearly indicate the presence of large-scale separation, in contrast to the pre-stalled case where the flow is still attached at the mid-chord. Finally, Fig. 15(f) shows further growth in the extent of the separated region as the angle-of-attack is increased to
$17^\circ $
case of Fig. 15(e). At the latter angle-of-attack, the boundary layer profiles at both chordwise locations clearly indicate the presence of large-scale separation, in contrast to the pre-stalled case where the flow is still attached at the mid-chord. Finally, Fig. 15(f) shows further growth in the extent of the separated region as the angle-of-attack is increased to
![]() $\alpha = 22^\circ $
.
$\alpha = 22^\circ $
.
8.0 Far-field sound from Amiet’s model
This section presents a theoretical prediction of the far-field sound radiated by the NACA 16-616 and NACA 0012 aerofoils, derived using Amiet’s model with back-scattering correction from Roger and Moreau [Reference Roger and Moreau3, Reference Amiet5]. Amiet’s model takes as an input a statistical description of the convecting surface pressure distribution with the key, underpinning, assumption that the turbulent velocity field is unaffected by the geometrical discontinuity at the trailing-edge, i.e. that the turbulence remains statistically stationary as it passes over the trailing-edge. In Amiet’s model, the far-field noise spectrum at an observer position
x
,
![]() $SPL\left( {f,\textbf{x}} \right)$
, is given by
$SPL\left( {f,\textbf{x}} \right)$
, is given by
where
![]() ${\phi _{pp}}\left( f \right)$
is the surface pressure spectrum at the trailing-edge,
${\phi _{pp}}\left( f \right)$
is the surface pressure spectrum at the trailing-edge,
![]() $l\left( f \right)$
is the spanwise coherence length, which quantifies the spanwise extent of turbulent structures in the boundary layer,
$l\left( f \right)$
is the spanwise coherence length, which quantifies the spanwise extent of turbulent structures in the boundary layer,
![]() $D\left( {f,\boldsymbol{{x}}} \right)$
is a radiation term, and
$D\left( {f,\boldsymbol{{x}}} \right)$
is a radiation term, and
![]() $\left| {\mathcal{L}\left( f \right)} \right|$
is the acoustically weighted aerofoil response function.
$\left| {\mathcal{L}\left( f \right)} \right|$
is the acoustically weighted aerofoil response function.
Figure 16 shows the prediction of the radiated far-field sound for the two aerofoils in the pre-stall and post-stall regime. As previously noted, the NACA 0012 data was collected in similar operating conditions as the NACA 16-616 aerofoil, and it was found to stall by a leading-edge mechanism at
![]() $14^\circ $
angle-of-attack [Reference Mayer, Kamliya Jawahar, Szoke, Showkat Ali and Azarpeyvand29, Reference Mayer, Zang and Azarpeyvand37]. Figure 16(a) compares the predicted radiated far-field sound in the pre-stall regime for each aerofoil and shows markedly different behaviour for each aerofoil. In the NACA 16-616 case of Fig. 16(a), the spectral behaviour is similar for the two pre-stall angles-of-attack presented, reflecting that in both cases the flow structures are very similar due to the small-scale separation that has occurred at the trailing-edge of the aerofoil. Conversely, the predicted radiated far-field sound of the NACA 0012 aerofoil differs greatly between the two pre-stall angles-of-attack, indicating that for this aerofoil, trailing-edge separation does not occur at low angles-of-attack and so the flow structures at the trailing-edge are different for the two cases presented. Direct comparison of the two aerofoils shows much higher sound pressure levels for the NACA 16-616 aerofoil, caused by the higher trailing-edge PSDs, as shown in Fig. 9, and the higher spanwise coherence lengths as shown in Fig. 13. Figure 16(c) and (d) compares the two aerofoils in the post-stall regime and, in contrast to the pre-stall regime, the spectral behaviour of the predicted radiated far-field sound is very similar for the two aerofoils. This reflects that both aerofoils have stalled via a dominant leading-edge separation mechanism for the angles-of-attack shown, leading to very similar separated flow characteristics and consequently similar radiated far-field sound.
$14^\circ $
angle-of-attack [Reference Mayer, Kamliya Jawahar, Szoke, Showkat Ali and Azarpeyvand29, Reference Mayer, Zang and Azarpeyvand37]. Figure 16(a) compares the predicted radiated far-field sound in the pre-stall regime for each aerofoil and shows markedly different behaviour for each aerofoil. In the NACA 16-616 case of Fig. 16(a), the spectral behaviour is similar for the two pre-stall angles-of-attack presented, reflecting that in both cases the flow structures are very similar due to the small-scale separation that has occurred at the trailing-edge of the aerofoil. Conversely, the predicted radiated far-field sound of the NACA 0012 aerofoil differs greatly between the two pre-stall angles-of-attack, indicating that for this aerofoil, trailing-edge separation does not occur at low angles-of-attack and so the flow structures at the trailing-edge are different for the two cases presented. Direct comparison of the two aerofoils shows much higher sound pressure levels for the NACA 16-616 aerofoil, caused by the higher trailing-edge PSDs, as shown in Fig. 9, and the higher spanwise coherence lengths as shown in Fig. 13. Figure 16(c) and (d) compares the two aerofoils in the post-stall regime and, in contrast to the pre-stall regime, the spectral behaviour of the predicted radiated far-field sound is very similar for the two aerofoils. This reflects that both aerofoils have stalled via a dominant leading-edge separation mechanism for the angles-of-attack shown, leading to very similar separated flow characteristics and consequently similar radiated far-field sound.

Figure 16. Prediction of radiated far-field sound pressure level based on Amiet’s model with different angle-of-attack of NACA 16-616 aerofoil and NACA 0012 aerofoil: (a) and (b) pre-stall, and (c) and (d) post-stall, respectively.
The predicted radiated far-field sound pressure levels of Fig. 16 show clearly the impact of aerofoil shape, via its impact on stalling behaviour, on the sound produced by an aerofoil. This dependency of far-field sound on aerofoil shape illustrates the need for high-fidelity near-field hydrodynamic data for a range of aerofoils in the development of generalised far-field noise models.
9.0 Conclusions and future work
Stall noise and its origins in the boundary layers of the aerofoil have been comparatively under researched and there is limited data on it. However, stall noise is an important consideration for a multitude of industries and so the development of a greater understanding of it, and of models for it, is of great interest. The primary objective of the present study was to generate new hydrodynamic near-field data from aerofoils not previously studied in detail, which will contribute to the development of more generalised noise models. To this end, this paper provides a summary of the near-field hydrodynamic behaviour of a NACA 16-616 aerofoil operating at a Reynolds number of
![]() $2.7 \times {10^5}$
over a range of angles-of-attack, from −
$2.7 \times {10^5}$
over a range of angles-of-attack, from −
![]() $5^\circ $
to
$5^\circ $
to
![]() $25^\circ $
, encompassing the pre-stall, stall and post-stall flow regimes. The high-fidelity near-field data provides a detailed insight into the near-field behaviour of NACA 16-616 aerofoil and shows different near-field spectral behaviour to other aerofoils such as the NACA 0012, particularly in the stall regime but also pre- and post-stall. This difference in behaviour is a result of the distinct separation mechanisms observed where, for the NACA 16-616 aerofoil, a secondary trailing-edge separation mechanism occurs within the pre-stall regime that is then subsumed by a dominant leading-edge separation that leads to the full stall of the aerofoil.
$25^\circ $
, encompassing the pre-stall, stall and post-stall flow regimes. The high-fidelity near-field data provides a detailed insight into the near-field behaviour of NACA 16-616 aerofoil and shows different near-field spectral behaviour to other aerofoils such as the NACA 0012, particularly in the stall regime but also pre- and post-stall. This difference in behaviour is a result of the distinct separation mechanisms observed where, for the NACA 16-616 aerofoil, a secondary trailing-edge separation mechanism occurs within the pre-stall regime that is then subsumed by a dominant leading-edge separation that leads to the full stall of the aerofoil.
The predicted far-field sound radiated by the NACA 16-616 and NACA 0012 aerofoils has been presented and compared, which clearly shows the significant effects of both aerodynamic stall and aerofoil shape on the trailing-edge noise. The noise spectra for each aerofoil in the pre-stall regime differ notably. For the NACA 16-616, the presence of the trailing-edge separation mechanism causes similar spectral decay for the pre-stall angles-of-attack, whereas for the NACA 0012 aerofoil, which does not experience the same trailing-edge separation mechanism, the behaviour varies with angles-of-attack, reflecting growth of the attached boundary layer. Moreover, in the pre-stall regime, the predicted noise of the cambered NACA 16-616 is consistently higher than the NACA 0012. Yet, for both aerofoils, the abrupt impact of the leading-edge stall mechanism leads to similar wholesale changes in the radiated sound with comparable magnitude. The significant impact of the flow separation behaviour of the aerofoil and the aerofoil shape on the radiated far-field sound illustrates the need for high-fidelity near-field hydrodynamic data for the development of generalised noise models.
Acknowledgements
The authors would like to acknowledge the financial support from the Engineering and Physical Sciences Research Council (EPSRC) for the present study via research Grant No. EP/R010846/1, and the first author would like to also acknowledge the support for the PhD studentship from Dowty Propellers and Embraer.