NOMENCLATURE
- FGAP
Flight gate assignment problem
- MRT
Mass rapid transit
- UL
The upper level programming model
- LL
The lower level programming model
Symbols
 $m$
$m$
pairs of flights
 $n$
$n$
number of gates
 ${y_{ik}}$
${y_{ik}}$
the decision variable, if
 ${y_{ik}} = 1$
indicates that flight
${y_{ik}} = 1$
indicates that flight  $i$
is docked at the gate
$i$
is docked at the gate  $k$
, otherwise
$k$
, otherwise  ${y_{ik}}=0$
${y_{ik}}=0$
 ${z_{ijk}}$
${z_{ijk}}$
the decision variable, if
 ${z_{ijk}} = 1$
indicates that flight
${z_{ijk}} = 1$
indicates that flight  $i$
is the previous flight of flight
$i$
is the previous flight of flight  $j$
parked at the same gate
$j$
parked at the same gate  $k$
$k$
 ${c_{ai}}$
(
${c_{ai}}$
( ${c_{gk}}$
)
${c_{gk}}$
)takes 1 or 2, which means the narrow and wide models of the flight and the gate, respectively
 $M$
$M$
a positive number large enough
 ${r_{jk}}$
${r_{jk}}$
the arrival time of flight
 $j$
at gate
$j$
at gate  $k$
$k$
 $\overline t $
$\overline t $
indicates the minimum buffer time between flights
 ${Q_i}$
${Q_i}$
the comprehensive difficulty factor of the
 $i$
flight
$i$
flight $\alpha (\beta )$
$\alpha (\beta )$
weight coefficient and
 $0 \le \alpha \le 1,0 \le \beta \le 1$
$0 \le \alpha \le 1,0 \le \beta \le 1$
 ${H_i}$
${H_i}$
the international/domestic type of flight
 $i$
$i$
 ${G_k}$
${G_k}$
the set of flight models that gate
 $k$
is allowed to call
$k$
is allowed to call $\overline H $
$\overline H $
international and domestic flight cross type values
 ${\tau _i}$
${\tau _i}$
the wide/narrow machine flight type and defines
 $\overline \tau $
$\overline \tau $
value of the wide body flight type
 ${\kappa _i}$
${\kappa _i}$
number of conflicts between flight
 $i$
and other flights
$i$
and other flights $\overline \kappa $
$\overline \kappa $
maximum number of time conflicts
 ${S_{kl}}$
${S_{kl}}$
the transfer time of gates
 ${p_{ij}}$
${p_{ij}}$
the number of passengers who transfer flight
 $i$
from flight
$i$
from flight  $j$
$j$
 ${R_{ik}}$
${R_{ik}}$
indicates that the flight
 $i$
occupies the idle time of the gate
$i$
occupies the idle time of the gate  $k$
$k$
 $\overline R $
$\overline R $
the average value of the flight idle time of the gate
 $k$
$k$
 ${W_k}({E_k})$
${W_k}({E_k})$
respectively represents the earliest (latest) time of the gate
 $k$
can stop the flight
$k$
can stop the flight
1.0 INTRODUCTION
The flight gate assignment problem (FGAP) is one of the most important problems operations managers face daily. The airport dispatching system is a complex system composed of airport buildings, gate groups and passenger flow. The complexity is mainly reflected in the coordination and rationality of flight scheduling and passenger transfer. The implementation of the airport dispatching system is closely related to the width of the gate position type, the type of landing flight, and the time interval between flights.
To solve this problem, scholars have studied many models and solutions. These solutions are mainly divided into two categories. The one is the establishment of expert systems(Reference Gosling1,Reference Su and Srihari2) , which are incorporated into the knowledge base system by analysing each influence factor. The other is to analyse flight gate assignment models and establish various mathematical models and solutions. Among them, Baron(Reference Baron3) simulated and analysed the effect of different boarding gate usage strategies on passenger walking distance. Yan and Chang(Reference Yan and Chang4) added a fixed buffer time between flights assigned to the gate and described the flight gate assignment problem as a multi-commodity network flow problem, which was solved by the shortest path method and the Lagrangian heuristic algorithm. Ding et al.(Reference Ding, Lim and Rodrigues5) focused on the over-constrained flight gate assignment, where the number of flights exceeds the number of gates available. And greedy algorithm and tabu search metaheuristic have been designed to solve the problem, which allows passengers flexibility in seeking good solutions, especially in the case of tight flight schedules. M. Seker and N. Noyan(Reference Seker and Noyan6) established a large-scale mixed integer programming model with uncertain arrival and departure times of flights and used the tabu search algorithm to solve this model. Liu et al.(Reference Liu, Chen and Liu7) established a quadratic 0-1 programming model that the objective function is to minimise the variance of idle time between flights, and the genetic algorithm is used to solve this model because genetic algorithm is effective for global searching. G. Sena Daş(Reference Sena DaŞ8) established new multi-objective models for increasing the shopping revenues of an airport operator. The multi-objective model assigns passengers to specific gates near shopping facilities and assigns flights to boarding gates to minimise the total passenger walking distance. In addition to the multi-objective model, Schaijk et al.(Reference van Schaijk and Visser9) proposed a new method to improve the robustness of the FGAP solution, and the approach is integrated into an existing multiple time slot FGAP model that based on a binary integer programming model. Simin et al.(Reference Xu, Jiang, Wang and Chen10) established a multi-objective assignment model to minimise the operating costs of airlines, passenger walking distance, and the probability of flight conflict, and the non-dominated sorting genetic algorithm-II (NSGA-II algorithm) is used in the simulation model to solve the multi-objective problem. Hence, flight gate assignment models mainly include integer linear programming models, mixed integer programming models, quadratic mixed 0-1 programming models, multi-objective models and stochastic models. The solving algorithms of these models mainly include a simplex method, branch and bound, sorting algorithm, graph theory, genetic algorithm, heuristic algorithms, TS, simulated annealing, hybridisation, and so on(Reference Bouras, Ghaleb, Suryahatmaja and Salem11–Reference Ulrich, Florian and Erwin14).
Through literature research, we found that the above papers mainly conduct independent research on airports, airlines and passengers, without considering the nested relationship among the three. There are few bilevel programming models for the flight gate assignment at airports (upper level), airlines, and passengers (lower level). In this paper, the overall variance of slack time between two consecutive flights at the same gate is minimised as the objective function of the upper level, and the number of passengers unsuccessfully transferred and passenger average transfer time are minimised as the objective function of the lower level. A bilevel programming model for a flight gate assignment problem is established, and the adaptive genetic algorithm is used to optimise the model. The simulation results show the occupation order and detailed assignment of each gate, as well as the values of the objective function of each level.
This paper is organised as follows. In Section 2, we give the formal definition of FGAP and the corresponding mathematical model, and review the related work. In Section 3, we propose the adaptive genetic algorithm for the bilevel programming model of the FGAP problem. In Section 4, we discuss the implementation of the proposed method, which includes a large number of computational experiments and comparisons. Finally, we summarise the whole paper and look forward to the future work in Section 5.
2.0 ESTABLISHMENT AND SOLUTION OF BILEVEL PROGRAMMING MODEL FOR FGAP
2.1 Description of the flight gate assignment problem (FGAP)
A flight gate optimal assignment is a complex process of multi-variable, multi-objective and multi-constrained optimisation, which includes many factors: the type of flight and gate (wide and narrow, international and domestic), the least time interval of the continuous parking between two flights at the same gate, the average travel time (cost) between passengers at gates, and the average time (cost) between entry and exit processing locations and gates. According to the current gate usage and the type of flight and gate, the command department of the airport dispatching system needs to assign each aircraft (flight) to the available gates, while maximising passenger convenience and the airport operational efficiency.
For the flight gate assignment, the following conditions must be met:
(1) Exclusivity: At the same time, a gate can serve only one flight.
(2) Uniqueness: A gate must be assigned to a flight (the temporary apron is considered as a gate) and only one is assigned.
(3) Security: Different flights use the same gate, and the time to enter and exit the gate must meet the corresponding safety time interval conditions.
(4) Suitability: The type of the flight assigned to the gate must match. The large-sized flights can only be assigned to the large-sized gates, the medium-sized flights can be assigned to large- or medium-sized gates, and small-sized flights can be assigned to large-, medium- or small-sized gates. International and domestic flights can be assigned only at the corresponding type of gate.
(5) Integrity: The flight assigned to gate shall not be less than the least time required for the docking flights. The landing and take-off of flights must be the same gate.
2.2 Mathematical model
In the bilevel programming model, there are two decision-making subjects of different levels, which is a system optimisation problem with a bilevel hierarchical structure. Different levels of decision-makers want to achieve different goals. The upper decision-maker has the right to control and guide the lower. The lower decision-maker chooses the optimal decision behaviour, which will affect the decision behaviour of the upper decision-maker.
The hierarchical structural relationship between the upper and lower level in the bilevel programming model is shown in Fig. 1, where the ellipse represents the decision-maker of the upper level and the rectangle with ellipse represents the decision-maker of the lower level.

Figure 1. Hierarchical structure of bilevel programming model.
In the FGAP problem, the decision-making bodies mainly include airports, airlines and passengers, and the three parties are at different levels. The airport issuer, as the flight gate assignment problem, has the right to determine the type of gate and the minimum buffer time setting between flights. The airlines and passengers make decisions based on the behaviour of the airport to achieve optimal income. So the airport is regarded as the upper level decision-maker, and the airline and passengers are regarded as the lower level decision-makers.
There are ![]() $m$
fixed gates available at an airport. The types are divided into wide (W), narrow (N), international (I), and domestic (D). The
$m$
fixed gates available at an airport. The types are divided into wide (W), narrow (N), international (I), and domestic (D). The ![]() $m + 1$
gate is temporary apron. The landing gate of a flight (one flight pair) must be the same as the gate of the take-off, and the types of flight are divided into wide (W), narrow (N), international (I), and domestic (D). Flights takes more than 5 hours from landing to departure, and they needs to be assigned to the temporary apron after the passenger gets off the plane and the unloading is completed (the apron can only park the flight).
$m + 1$
gate is temporary apron. The landing gate of a flight (one flight pair) must be the same as the gate of the take-off, and the types of flight are divided into wide (W), narrow (N), international (I), and domestic (D). Flights takes more than 5 hours from landing to departure, and they needs to be assigned to the temporary apron after the passenger gets off the plane and the unloading is completed (the apron can only park the flight).
According to the flight gate assignment conditions, the following constraints are established.
(1) The uniqueness of the gate used
(1) \begin{equation}\sum\limits_{i = 1}^n {{y_{ik}}} = 1.\end{equation}
\begin{equation}\sum\limits_{i = 1}^n {{y_{ik}}} = 1.\end{equation}
(2) Narrow-type flights can assign to the gate, and the constraint established is
(2) \begin{equation}{c_{ai}} - {c_{gk}} + {y_{ik}}M \ge 0.\end{equation}
\begin{equation}{c_{ai}} - {c_{gk}} + {y_{ik}}M \ge 0.\end{equation}
(3) Whether the flights
 $i$
and
$i$
and  $j$
can be assigned at the same gate
$j$
can be assigned at the same gate  $k$
, if
$k$
, if ${({d_{jk}} - {r_{ik}})({d_{ik}} - {r_{jk}}) > 0}$
, then
(3)
${({d_{jk}} - {r_{ik}})({d_{ik}} - {r_{jk}}) > 0}$
, then
(3) \begin{equation}{y_{ik}} + {y_{jk}} \le 1.\end{equation}
\begin{equation}{y_{ik}} + {y_{jk}} \le 1.\end{equation}
(4) (4) The constraint is established according to the security interval, that is, the interval between two flights adjacent to each other at the same gate should be no less than the security interval of
 $\bar t$
minutes, and the constraint is
(4)
$\bar t$
minutes, and the constraint is
(4) \begin{equation}(1 - {z_{ijk}})M + {r_{jk}} - {d_{ik}} \ge \bar t.\end{equation}
\begin{equation}(1 - {z_{ijk}})M + {r_{jk}} - {d_{ik}} \ge \bar t.\end{equation}
(5) The uniqueness of two consecutive flights assigned at the same gate, and must contain two flights at the gate
(5) \begin{equation}\sum\limits_{k \in S} {\sum\limits_{i \in F} {{z_{ijk}}} } = 1,\end{equation}
(6)
\begin{equation}\sum\limits_{k \in S} {\sum\limits_{i \in F} {{z_{ijk}}} } = 1,\end{equation}
(6) \begin{equation}{y_{ik}} + {y_{jk}} - 2{z_{ijk}} \ge 0.\end{equation}
\begin{equation}{y_{ik}} + {y_{jk}} - 2{z_{ijk}} \ge 0.\end{equation}
(6) According to the priority of the flights, we first assign the difficult-to-assign flight to the available gate, and then the next level flights are assigned to the available gate according to the difficulty level. Finally, we can give priority to the gates that have been used before, and so on.
The difficulty of assigning flights is related to the time conflict of flights and the type of flights. The more times the flight conflicts with other flight times, the more difficult it is to assign flights. The wider the machine type of flight, the harder it is to assign flights. We should give higher priority in assigning the number of flight conflicts and the type of flight. The difficulty coefficient is used to measure the assignment difficulty of the gate, and difficulty factor is defined as follows
where  ${H_i} = \begin{cases} 1,& {\rm{flight\ type\ }II,DD}\\ 2, & {\rm{flight\ type\ }ID,DI} \end{cases} $
,
${H_i} = \begin{cases} 1,& {\rm{flight\ type\ }II,DD}\\ 2, & {\rm{flight\ type\ }ID,DI} \end{cases} $
, ${\tau _i} = \begin{cases} 1, & {\rm{flight\ type\ }N}\\ 2, & {\rm{flight\ type\ }W} \end{cases}$
.
${\tau _i} = \begin{cases} 1, & {\rm{flight\ type\ }N}\\ 2, & {\rm{flight\ type\ }W} \end{cases}$
.
It can be seen from Equation (7) that the smaller ![]() $\alpha $
is the smaller the proportion of flight types in the difficulty coefficient, and it is the greater the proportion of flight conflicts. Priority is given to flights with a large number of flight conflicts and small flight types, which is not conducive to flights with fewer flight conflicts and larger categories. Similarly, the larger
$\alpha $
is the smaller the proportion of flight types in the difficulty coefficient, and it is the greater the proportion of flight conflicts. Priority is given to flights with a large number of flight conflicts and small flight types, which is not conducive to flights with fewer flight conflicts and larger categories. Similarly, the larger ![]() $\alpha $
is the larger the proportion of the body type in the difficulty coefficient, and it is the smaller the proportion of flight conflict. Priority is given to flights with larger and less conflict, which is not conducive to flights with smaller and more conflict. In the solution, the
$\alpha $
is the larger the proportion of the body type in the difficulty coefficient, and it is the smaller the proportion of flight conflict. Priority is given to flights with larger and less conflict, which is not conducive to flights with smaller and more conflict. In the solution, the ![]() $\alpha $
value can be adjusted to get the best assignment plan.
$\alpha $
value can be adjusted to get the best assignment plan.
As a government agency, the airport is responsible for providing services to the society. It pursues the maximisation of social welfare and maximise the use of resources. The upper-level airport revenue is measured by the delay of launching all flight pairs. At this time, the maximisation of airport revenue is converted into the minimum overall variance of slack time between two consecutive aircraft at the same gate(Reference Zheng, Hu and Zhang15). This paper considers the time difference between the first flight and the last flight at each gate, as well as the time interval between two consecutive flights at the same gate. The upper level programming model (UL) is
 \begin{align}\min {F_1} & = \sum\limits_{i = 1}^n {\sum\limits_{k = 1}^m {{{({R_{ik}} - \bar R)}^2}} } \nonumber\\[5pt]
s.t.{R_{jk}} & = ({r_{ik}} - {W_k}),\ j = \min (\,j),\ j \in \left\{ {j|{y_{jk}} = 1} \right\}\nonumber\\[5pt]
{R_{nk}} & = ({E_k} - {d_{ik}}),i = \max (i),i \in \left\{ {i|{y_{ik}} = 1} \right\}\nonumber\\[5pt]
{R_{ik}} & = ({r_{jk}} - {d_{ik}}),\forall i,j,k \in \left\{ {(i,j,k)|{z_{ijk}} = 1} \right\}\nonumber\\[5pt]
\bar R & = \frac{{\sum\limits_{k = 1}^m {({E_k} - {W_k})} - \sum\limits_{i = 1}^n {({d_{ik}} - {d_{jk}})} }}{{n + m}}\end{align}
\begin{align}\min {F_1} & = \sum\limits_{i = 1}^n {\sum\limits_{k = 1}^m {{{({R_{ik}} - \bar R)}^2}} } \nonumber\\[5pt]
s.t.{R_{jk}} & = ({r_{ik}} - {W_k}),\ j = \min (\,j),\ j \in \left\{ {j|{y_{jk}} = 1} \right\}\nonumber\\[5pt]
{R_{nk}} & = ({E_k} - {d_{ik}}),i = \max (i),i \in \left\{ {i|{y_{ik}} = 1} \right\}\nonumber\\[5pt]
{R_{ik}} & = ({r_{jk}} - {d_{ik}}),\forall i,j,k \in \left\{ {(i,j,k)|{z_{ijk}} = 1} \right\}\nonumber\\[5pt]
\bar R & = \frac{{\sum\limits_{k = 1}^m {({E_k} - {W_k})} - \sum\limits_{i = 1}^n {({d_{ik}} - {d_{jk}})} }}{{n + m}}\end{align}
Airlines generally pursue profit maximisation, which is to minimise the number of unsuccessful transfer passengers. The revenue of the airline is mainly from the consumption of the passengers, and the fixed cost of the flight is removed. The more passengers who successfully board the flight (minimum passenger transfer failures), the higher the airline’s revenue will be
As a service recipient, passengers pursue the maximisation of the utility function. The passenger’s utility function can be characterised by the passenger’s satisfaction with the service of the airport and the airline. In this paper, we improve the passenger’s satisfaction by minimum passenger’s average transfer time
As a rational individual, airlines and passengers pursue profit maximisation and utility maximisation respectively. The lower level model (LL) of the bilevel programming model is
 \begin{equation} \begin{array}{l}\min {F_2} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{p_{ij}}} } - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^m {\sum\limits_{l = 1}^m {[{p_{ij}}(1 - {y_{ik}})(1 - {y_{jl}}) + {p_{ij}}{y_{ik}}(1 - {y_{jl}}) + {p_{ij}}(1 - {y_{ik}}){y_{jl}}]} } } } \\[12pt] \min {F_3} = {{\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^m {\sum\limits_{l = 1}^m {{S_{kl}}\,{p_{ij}}\,{y_{ik}}\,{y_{jl}}} } } } } \bigg/ {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{p_{ij}}} } }}\\[12pt] \left\{ \begin{array}{l@{\quad}l} s.t. & \sum\limits_{k = 1}^{m + 1} {{y_{ik}}} = 1\\[10pt] & {H_i} \in {G_j}\\[4pt] & {c_{ai}} - {c_{gk}} + {y_{ik}}M \ge 0\\[4pt] & {y_{ik}} + {y_{jk}} \le 1\\[4pt] & (1 - {z_{ijk}})M + {r_{jk}} - {d_{ik}} \ge \bar t\\[4pt] & \sum\limits_{k \in S} {\sum\limits_{i \in F} {{z_{ijk}}} = 1} \\[10pt] & {y_{ik}} + {y_{jk}} - 2{z_{ijk}} \ge 0\\[4pt] & {y_{ik}},\;{y_{jl}},\;{z_{ijk}} \in \left\{ {{\rm{0,}}\;{\rm{1}}} \right\}\end{array} \right.\end{array}.\end{equation}
\begin{equation} \begin{array}{l}\min {F_2} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{p_{ij}}} } - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^m {\sum\limits_{l = 1}^m {[{p_{ij}}(1 - {y_{ik}})(1 - {y_{jl}}) + {p_{ij}}{y_{ik}}(1 - {y_{jl}}) + {p_{ij}}(1 - {y_{ik}}){y_{jl}}]} } } } \\[12pt] \min {F_3} = {{\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^m {\sum\limits_{l = 1}^m {{S_{kl}}\,{p_{ij}}\,{y_{ik}}\,{y_{jl}}} } } } } \bigg/ {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{p_{ij}}} } }}\\[12pt] \left\{ \begin{array}{l@{\quad}l} s.t. & \sum\limits_{k = 1}^{m + 1} {{y_{ik}}} = 1\\[10pt] & {H_i} \in {G_j}\\[4pt] & {c_{ai}} - {c_{gk}} + {y_{ik}}M \ge 0\\[4pt] & {y_{ik}} + {y_{jk}} \le 1\\[4pt] & (1 - {z_{ijk}})M + {r_{jk}} - {d_{ik}} \ge \bar t\\[4pt] & \sum\limits_{k \in S} {\sum\limits_{i \in F} {{z_{ijk}}} = 1} \\[10pt] & {y_{ik}} + {y_{jk}} - 2{z_{ijk}} \ge 0\\[4pt] & {y_{ik}},\;{y_{jl}},\;{z_{ijk}} \in \left\{ {{\rm{0,}}\;{\rm{1}}} \right\}\end{array} \right.\end{array}.\end{equation}
It is important to note that the model (UL) variables are determined by the model (LL) variables, and the model (UL) variables ![]() ${R_{ik}}$
are related to the flight gate assignment. If the model (LL) variables
${R_{ik}}$
are related to the flight gate assignment. If the model (LL) variables ![]() ${z_{ijk}} = 1$
, then we can get the model (UL) variables
${z_{ijk}} = 1$
, then we can get the model (UL) variables ![]() ${R_{ik}}$
for all
${R_{ik}}$
for all ![]() $i,j,k \in \left\{ {(i,j,k)|{z_{ijk}} = 1} \right\}$
.
$i,j,k \in \left\{ {(i,j,k)|{z_{ijk}} = 1} \right\}$
.
Among them, the transfer time of gates (![]() ${S_{kl}}$
) include MRT time, shortest flow time and walking time of transit passengers. Passengers are divided into originating passengers, transfer passengers and final passengers. Since the time of departure and final passengers can be adjusted by themselves, this paper considers only transfer passengers in the airport.
${S_{kl}}$
) include MRT time, shortest flow time and walking time of transit passengers. Passengers are divided into originating passengers, transfer passengers and final passengers. Since the time of departure and final passengers can be adjusted by themselves, this paper considers only transfer passengers in the airport.
3.0 SOLUTION BASED ON ADAPTIVE GENETIC ALGORITHM
Bilevel programming problem is an NP-hard problem in nature, which is quite difficult to solve. The nonlinear bilevel programming model established in this paper is more complicated to solve. Among many algorithms, genetic algorithm has a strong general framework for solving complex problems. The algorithm does not depend on the neighbourhood of the problems. The algorithm has strong robustness, global searchability and internal parallel solution.
3.1 Encoding scheme and decoding procedure
As we all know, a good encoding way is very important since it significantly affects all following steps of genetic algorithm. After initialisation, the encoding scheme and the decoding program adopt the three-string encoding that solves this kind of special strong constraint problem, which are introduced as follows.
Step 1. If the flight i is assigned to gate k, the gate k is located at the i position in the string.
Step 2. (Sequence-oriented representation) All flights are ordered according to the difficulty of the assigned gate and assigned to the assigned gate according to the difficulty of the assigned gate.
Step 3. (Partition-oriented representation) Separators are introduced in the sequence-oriented representation to assign the flight into gates.
During the initialisation and encoding process, we assign the obtained flight sequence to gate. For example, as shown in Fig. 2, we need to divide the flight sequence into sections, each of which represents the flight order assigned to a particular gate. The encoding and decoding process and flight assignment results are shown in Fig. 3.

Figure 2. Decoding procedure.
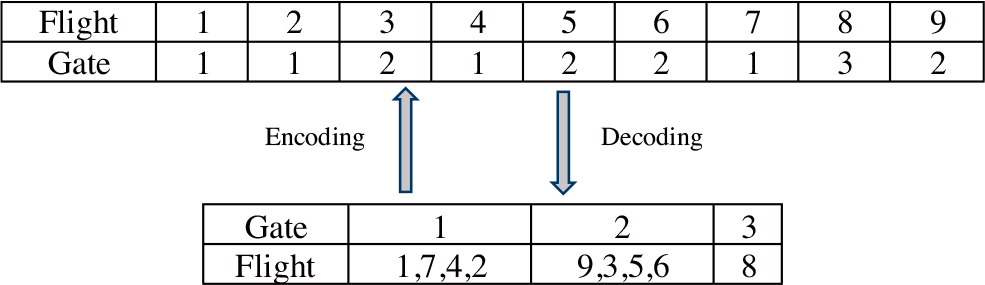
Figure 3. Encoding and decoding process.
3.2 Individual fitness evaluation
The genetic algorithm determines the probability of each individual in the current population, which is inherited into the next generation group by a probability proportional to the individual fitness value. If the fitness value of all individuals must be not less than 0, then the individual’s fitness value can be represented by its objective function value. Otherwise, the transformation relationship between the objective function value and the individual fitness value by the following formula
 \begin{equation}{F_{fit}} = \frac{{\rm{1}}}{{\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^m {{{({R_{ik}} - \bar R)}^2}} } }}.\end{equation}
\begin{equation}{F_{fit}} = \frac{{\rm{1}}}{{\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^m {{{({R_{ik}} - \bar R)}^2}} } }}.\end{equation}
3.3 Genetic operator
(1) The selection operator applies the roulette wheel selection to select individuals from the group to p(t) obtain the group p(t +1), and it is executed with the following three steps.
Step 1. Calculate the sum of the fitness values of all individuals in the population
 $P(t)$
.
$P(t)$
.Step 2. Calculate the relative fitness value of each individual in the population
 $P(t)$
, which is the probability that each individual inherits to the next generation population.
$P(t)$
, which is the probability that each individual inherits to the next generation population.Step 3. Determine the number of times each individual has been selected by using roulette (i.e. a random number between 0 and 1).
(2) Crossover operator is one of the main steps for generating new individuals. A special type of crossover operator is used to solve this practical problem for the characteristics of the bilevel model of flight gate assignment. At the same time, in order to ensure that the generated sub-individual is feasible, the upper-level decision variables are made into the partial mapping crossover operator (PMX) of the following form:
Step 1. Randomly select two split points in the string, and the substring defined by the two split points is called a map segment.
Step 2. Exchange substrings between two parents to produce prototype offspring.
Step 3. Remove all existing symbols in all substrings of the second parent, and the remaining sequences contain the symbols needed by the prototype offspring.
Step 4. Generate an offspring by placing the symbol in the left-to-right order into the remaining space of the prototype offspring.
(3) A mutation operator is used to improve the local searchability of the genetic algorithm and maintain the diversity of the population. This paper uses the non-uniform mutation operation as follows
(13) \begin{equation}{s_0}(k) = \left\{ \begin{array}{l}s(k) + \mu \left( {{s_{ub}}(k) - s(k)} \right),\quad random\left\{ {0,1} \right\} = 0,\\[5pt]
s(k) - \mu ({s(k) - {s_{lb}}(k)} ),\quad \,random\left\{ {0,1} \right\} = 1,\end{array} \right..\end{equation}
\begin{equation}{s_0}(k) = \left\{ \begin{array}{l}s(k) + \mu \left( {{s_{ub}}(k) - s(k)} \right),\quad random\left\{ {0,1} \right\} = 0,\\[5pt]
s(k) - \mu ({s(k) - {s_{lb}}(k)} ),\quad \,random\left\{ {0,1} \right\} = 1,\end{array} \right..\end{equation}
Where ![]() ${s_{ub}}(k)$
and
${s_{ub}}(k)$
and ![]() ${s_{lb}}(k)$
are the upper and lower bounds of the variable
${s_{lb}}(k)$
are the upper and lower bounds of the variable ![]() ${S_{ik}}$
respectively, and
${S_{ik}}$
respectively, and ![]() $\mu \in \left[ {0,1} \right]$
is randomly generated.
$\mu \in \left[ {0,1} \right]$
is randomly generated.
3.4 Crossover probability and mutation probability
The crossover probability ![]() ${p_c}$
and mutation probability
${p_c}$
and mutation probability ![]() ${p_m}$
are the key factors of the genetic algorithm. In addition, the model is a kind of problem with strong constraints. The adaptive method is used to determine
${p_m}$
are the key factors of the genetic algorithm. In addition, the model is a kind of problem with strong constraints. The adaptive method is used to determine ![]() ${p_c},{p_m}$
, so that the individual with the greatest fitness in the population, the probability of crossover and excellent individuals can inherit to the next generation and improve the possibility of solution. The algorithm jumps out of local optimum and achieves global optimum (see Ref. (Reference Wang, Wang, Wan and Jia16)).
${p_c},{p_m}$
, so that the individual with the greatest fitness in the population, the probability of crossover and excellent individuals can inherit to the next generation and improve the possibility of solution. The algorithm jumps out of local optimum and achieves global optimum (see Ref. (Reference Wang, Wang, Wan and Jia16)).
 \begin{equation}{p_c} = \left\{ \begin{array}{l@{\quad}l}{p_{c1}} - \frac{{\left( {{p_{c1}} \,{-}\, {p_{c2}}} \right)\left( {f' \,{-}\, \bar f} \right)}}{{{f_{\max }} \,{-}\, \bar f}},& f' \ge\, \bar f,\\[10pt]
{p_{c1}},& f' < \,\bar f, \end{array}\right. \quad {p_m} = \left\{ \begin{array}{l@{\quad}l}{p_{m1}} - \frac{{\left( {{p_{m1}} \,{-}\, {p_{m2}}} \right)\left( {f' \,{-}\, \bar f} \right)}}{{{f_{\max }} \,{-}\, \bar f}},& f' \ge\, \bar f,\\[10pt]
{p_{m1}}, & f' <\, \bar f\end{array}\right.\end{equation}
\begin{equation}{p_c} = \left\{ \begin{array}{l@{\quad}l}{p_{c1}} - \frac{{\left( {{p_{c1}} \,{-}\, {p_{c2}}} \right)\left( {f' \,{-}\, \bar f} \right)}}{{{f_{\max }} \,{-}\, \bar f}},& f' \ge\, \bar f,\\[10pt]
{p_{c1}},& f' < \,\bar f, \end{array}\right. \quad {p_m} = \left\{ \begin{array}{l@{\quad}l}{p_{m1}} - \frac{{\left( {{p_{m1}} \,{-}\, {p_{m2}}} \right)\left( {f' \,{-}\, \bar f} \right)}}{{{f_{\max }} \,{-}\, \bar f}},& f' \ge\, \bar f,\\[10pt]
{p_{m1}}, & f' <\, \bar f\end{array}\right.\end{equation}
where ![]() ${f_{\max }}$
is the maximal fitness value of the population,
${f_{\max }}$
is the maximal fitness value of the population, ![]() $\bar f$
is the individual average fitness value of the population, and
$\bar f$
is the individual average fitness value of the population, and ![]() $f'$
is the maximal fitness value of the two crossover individuals.
$f'$
is the maximal fitness value of the two crossover individuals. ![]() ${p_{c1}}$
,
${p_{c1}}$
, ![]() ${p_{c2}}$
,
${p_{c2}}$
, ![]() ${p_{m1}}$
, and
${p_{m1}}$
, and ![]() ${p_{m2}}$
are constants.
${p_{m2}}$
are constants.
3.5 Algorithm steps
In this paper, the algorithm steps are as follows(Reference Yang17–Reference Lederer and Altstadt19):
Step 1. Initialisation, and the algorithm parameters are set: the size of the population
 ${f_{\max }}$
is
${f_{\max }}$
is  $M'$
, the number of times
$M'$
, the number of times  $T$
.
$T$
.Step 2. Initialize the population, the upper level randomly generate
 ${R_{ik}}$
, substitutes the lower level and solves the lower level model, and obtains the optimal solution
${R_{ik}}$
, substitutes the lower level and solves the lower level model, and obtains the optimal solution  $Y = {({y_{ik}})_{n \times m}}$
. Then point
$Y = {({y_{ik}})_{n \times m}}$
. Then point  $\left( {{R_{ik}},Y} \right)$
is the individual of the initial population. When enough individuals are generated, the iterator is recorded as
$\left( {{R_{ik}},Y} \right)$
is the individual of the initial population. When enough individuals are generated, the iterator is recorded as  $t = 0$
, and go to Step 3.
$t = 0$
, and go to Step 3.Step 3. Calculate the individual fitness value. We use the reciprocal of the upper-level objective function as the fitness function (see Equation (12)) to calculate the average fitness value
 $\bar f$
and the maximum fitness value
$\bar f$
and the maximum fitness value  $f'$
of all individuals in the population
$f'$
of all individuals in the population  $P( t)$
.
$P( t)$
.Step 4. Retain the current optimal solution. In Step 3, the individual with the maximum fitness value is the current optimal solution in the population. Otherwise, the current optimal solution remains unchanged.
Step 5. Calculate the crossover probability and mutation probability (see Equation (14)).
Step 6. The selection operator applies the roulette wheel selection to select individuals from the group to
 $P(t)$
obtain the group
$P(t)$
obtain the group  $P( {t + 1})$
.
$P( {t + 1})$
.Step 7. Perform crossover and mutation operations on the population
 $P( {t + 1} )$
.
$P( {t + 1} )$
.Step 8. If
 $t + 1 \ge T$
, the algorithm terminates and retains the current best individual as the optimal solution for the bilevel programming problem. Otherwise, let
$t + 1 \ge T$
, the algorithm terminates and retains the current best individual as the optimal solution for the bilevel programming problem. Otherwise, let  $t = t + 1$
and return to Step 3.
$t = t + 1$
and return to Step 3.
4.0 NUMERICAL EXPERIMENT
4.1 Data processing
The airport has 28 gates in the terminal building and 41 gates in the satellite hall (![]() $n = 69$
). The terminal building can arrive, depart, entry and exit processing and wait for departure. The satellite hall can wait for departure, but there is no entry and exit processing. There is an MRT line between the terminal building and the satellite hall, 8 minutes one way, and the schematic diagram of the terminal building and the satellite hall is shown in Fig. 4. According to the departure area of the airport, we can get the transfer time matrix
$n = 69$
). The terminal building can arrive, depart, entry and exit processing and wait for departure. The satellite hall can wait for departure, but there is no entry and exit processing. There is an MRT line between the terminal building and the satellite hall, 8 minutes one way, and the schematic diagram of the terminal building and the satellite hall is shown in Fig. 4. According to the departure area of the airport, we can get the transfer time matrix ![]() ${S_{kl}}$
(
${S_{kl}}$
(![]() ${S_{kl}} = {\left( {{s_{kl}}} \right)_{69 \times 69}}$
,
${S_{kl}} = {\left( {{s_{kl}}} \right)_{69 \times 69}}$
, ![]() ${s_{kl}} \in \left[ {25,81} \right]$
) between the gates. The types of gates are domestic/international, arrival/departure, wide/narrow aircraft, and the same type of flight. The type of flight and gate can be matched, but narrow-body flights can be parked at boarding gates that are wide or narrow. Minutes of idle time between two flights assigned at the same gate is not less than 45(
${s_{kl}} \in \left[ {25,81} \right]$
) between the gates. The types of gates are domestic/international, arrival/departure, wide/narrow aircraft, and the same type of flight. The type of flight and gate can be matched, but narrow-body flights can be parked at boarding gates that are wide or narrow. Minutes of idle time between two flights assigned at the same gate is not less than 45(![]() $\bar t = 45$
). The airport has a temporary apron for aircraft unassigned to the fixed gate. The data includes data for 19, 20 and 21 January of 2018, and the daily flight record is the same, which analyses 303 pairs of flights (
$\bar t = 45$
). The airport has a temporary apron for aircraft unassigned to the fixed gate. The data includes data for 19, 20 and 21 January of 2018, and the daily flight record is the same, which analyses 303 pairs of flights (![]() $m = 303$
). The 2,751 passengers who arrived at the airport on the 20th and left the airport on the 20th.
$m = 303$
). The 2,751 passengers who arrived at the airport on the 20th and left the airport on the 20th.
Flight gate assignment is to assign a pair of flights (arrival and departure flights) to gate, each with a domestic/international (D/I) and wide body/narrow body machine (W/N) types, the specific classification is shown in Tables 1 and 2. For example, looking at “DDN”, the first part (“D”) indicates the type of the arrival flight is domestic, the second part (“D”)indicates the type of the departure flight is domestic, the third part (“N”) indicates the machine type of flight is narrow body, and the “X” indicates that both domestic (D) and international (I) can be placed.
Table 1 Classification of gate types
Table 2 Flight type division


Figure 4. Schematic diagram of the satellite hall relative to the terminal building.
4.2 Model results
This paper takes the population size as ![]() $M = 200$
, the iterations as
$M = 200$
, the iterations as ![]() $T = 100$
, crossover probability and mutation probability constant as
$T = 100$
, crossover probability and mutation probability constant as ![]() ${p_{c1}} = 0.9$
,
${p_{c1}} = 0.9$
, ![]() ${p_{c2}} = 0.6$
,
${p_{c2}} = 0.6$
, ![]() ${p_{m1}} = 0.1$
,
${p_{m1}} = 0.1$
, ![]() ${p_{m2}} = 0.01$
. The convergence rate of genetic algorithm is not only related to genetic algebra and population size, but also to the individual quality of the initial population. The larger the fitness of the initial population and the smaller the constraints are, the faster the algorithm converges will be. The larger the population size, the stronger the diversity of the organism, the better the effect of the algorithm converges to the global optimal solution. When the population size is 200 and 250, the result is almost the same, and the result is that the algorithm with a size of 200 runs less time.
${p_{m2}} = 0.01$
. The convergence rate of genetic algorithm is not only related to genetic algebra and population size, but also to the individual quality of the initial population. The larger the fitness of the initial population and the smaller the constraints are, the faster the algorithm converges will be. The larger the population size, the stronger the diversity of the organism, the better the effect of the algorithm converges to the global optimal solution. When the population size is 200 and 250, the result is almost the same, and the result is that the algorithm with a size of 200 runs less time.
The running time of the bilevel programming model by the adaptive genetic algorithm is 19.207 seconds, and the algorithm is relatively stable after 20 iterations. Minimum overall variance of slack time between flights of the upper level objective function, the lower level objective minimum passenger’s average transfer time and minimum unsuccessful passengers are optimal, and the convergence process of the best fitness and average fitness represented by the three objective functions are shown in the Fig. 5(a)– (c).

Figure 5. Algorithm process convergence diagram.
Through the numerical experiment, the flight gate assignment model and the use time of the gate and the waiting time can be obtained. It can be seen from the results that the optimisation result of the upper objective idle time is 83.396 minutes, the lower level the number of successful transfer passengers is 2,280, and the success rate is 82.879%. The minimum passenger’s average transfer time is 58.461 minutes within the transfer time interval ![]() $\left[ {25,\ 81} \right]$
minutes. The minimum number of gates used was 62, and the ratio of unused gates was 10.145%. The maximum number of flights successfully assigned to gates was 274 flights, and the ratio of the flights were successfully assigned to gates is 90.429%. The flights that did not successfully assign to gates were mainly narrow flights, and there are 16 “DIN” flights and 13 “IDN” flights that did not successfully assign to gates. When the algorithm reaches stability, a detailed schedule of each gate is obtained. According to Table 3, the flight gate map can be drawn as shown in Fig. 6, where the number in the figure represents the corresponding flight pair. Due to the length of the paper, schedule of only some gates is given in the text as shown in Table 3.
$\left[ {25,\ 81} \right]$
minutes. The minimum number of gates used was 62, and the ratio of unused gates was 10.145%. The maximum number of flights successfully assigned to gates was 274 flights, and the ratio of the flights were successfully assigned to gates is 90.429%. The flights that did not successfully assign to gates were mainly narrow flights, and there are 16 “DIN” flights and 13 “IDN” flights that did not successfully assign to gates. When the algorithm reaches stability, a detailed schedule of each gate is obtained. According to Table 3, the flight gate map can be drawn as shown in Fig. 6, where the number in the figure represents the corresponding flight pair. Due to the length of the paper, schedule of only some gates is given in the text as shown in Table 3.

Figure 6. Flight gate assignment map.
Table 3 Flight arrangement for partial gates

It can be seen from the results that 28 gates are used at the terminal building, 34 gates are used at the satellite hall, and the average occupancy rates of the gates at the terminal building and satellite hall respectively are 53.671% and 41.115%. The time to occupancy ratio of 69 gates, blue indicates the gate of the terminal building, and orange indicates the gate of the satellite hall. See Fig. 7.

Figure 7. The occupation time ratio of the gate.
4.3 Comparison with other algorithms
The convergence rate of genetic algorithm is not only related to the genetic algebra and population size, but also to the individual quality of the initial population. The higher the adaptive value of the initial population, the lower the constraint value, and the faster the convergence rate of the algorithm. At the same time, the larger the population size, the stronger the biodiversity, and the better the effect of convergence to the global optimal. However, when the optimal solution with a population size of 200 is the same as the optimal solution with a population size of 250, it is obvious that the algorithm with a population size of 200 has a shorter running time. In this paper, the selection of adaptive methods for crossover probability and genetic probability makes the solution of the algorithm better jump out of the local optimal and achieve the global optimal. The algorithm in this paper is compared with other algorithms in the reference. The results are shown in Table 4. The experimental results show that the results of the model and algorithm established in this paper are relatively better, and the convergence rate is faster.
Table 4 Comparison of algorithm optimization results

5.0 CONCLUSION
In this paper, we have considered the minimisation of two criteria to solve the flight gate assignment problem. Taking the minimum overall variance of slack time between two consecutive aircraft at the same gate as the upper level objective and the minimum passenger transfer failure and the minimum passenger average transfer time as the lower level objective, a bilevel programming model of FGDP is established. The crossover probability and mutation probability in the algorithm are determined by an adaptive method, so that the algorithm jumps out of the local optimum to achieve global optimal solution. Through the model validation, the optimal value for the upper level is 83.396 minutes. For the lower level, the flights successfully assign to gate at 90.429%, and there are 471 passengers transfer failed and the transfer success rate is 82.879%. The passengers average transfer time is 58.461 minutes, and the average occupancy rates of the used gates of the terminal building and satellite hall were 53.671% and 41.115%, respectively. It can be seen that the models and algorithms established in this paper are effective for the flight gate assignment.
Flight gate assignment is a complex problem. This paper discusses only the static assignment problem. Further research is needed on the dynamic assignment of parking spaces such as flight delays.













