Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hsing, Tailen
and
Teugels, J. L.
1989.
Extremal properties of shot noise processes.
Advances in Applied Probability,
Vol. 21,
Issue. 03,
p.
513.
Jensen, Jens L.
and
Johansson, Björn
1990.
The extremal family generated by the Yule process.
Stochastic Processes and their Applications,
Vol. 36,
Issue. 1,
p.
59.
Wang, Soujin
1990.
Saddlepoint approximations in resampling analysis.
Annals of the Institute of Statistical Mathematics,
Vol. 42,
Issue. 1,
p.
115.
Jensen, J. L.
1991.
Saddlepoint approximations to the distribution of the total claim amount in some recent risk models.
Scandinavian Actuarial Journal,
Vol. 1991,
Issue. 2,
p.
154.
Jensen, Jens Ledet
1991.
Saddlepoint expansions for sums of Markov dependent variables on a continuous state space.
Probability Theory and Related Fields,
Vol. 89,
Issue. 2,
p.
181.
Jensen, Jens Ledet
1991.
A Large Deviation-Type Approximation for the “Box Class” of Likelihood Ratio Criteria.
Journal of the American Statistical Association,
Vol. 86,
Issue. 414,
p.
437.
Jensen, J.L.
and
Kristensen, L.B.
1991.
Saddlepoint approximations to exact tests and improved likelihood ratio tests for the gamma distribution.
Communications in Statistics - Theory and Methods,
Vol. 20,
Issue. 4,
p.
1515.
Jensen, Jens Ledet
1991.
Uniform Saddlepoint Approximations and Log-Concave Densities.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 53,
Issue. 1,
p.
157.
Barndorff-Nielsen, Ole E.
and
Klüppelberg, Claudia
1992.
A note on the tail accuracy of the univariate saddlepoint approximation.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 1,
Issue. 1,
p.
5.
1992.
Discussion of the Paper by Pierce and Peters.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 54,
Issue. 3,
p.
725.
Nishii, Ryuei
1993.
Convergence of the Gram-Charier expansion after the normalizing Box-Cox transformation.
Annals of the Institute of Statistical Mathematics,
Vol. 45,
Issue. 1,
p.
173.
Wood, Andrew T. A.
Booth, James G.
and
Butler, Ronald W.
1993.
Saddlepoint Approximations to the CDF of Some Statistics with Nonnormal Limit Distributions.
Journal of the American Statistical Association,
Vol. 88,
Issue. 422,
p.
680.
Homble, P.
and
Mccormick, William P.
1993.
Tail areas for randomly stopped sums defined on a Markov chain.
Communications in Statistics. Stochastic Models,
Vol. 9,
Issue. 4,
p.
563.
Nishii, Ryuei
1994.
Convergence of the gram-charier expansion of the signed log likelihood ratio.
Communications in Statistics - Theory and Methods,
Vol. 23,
Issue. 9,
p.
2605.
Barndorff-Nielsen, Ole E.
and
Schmidli, Hanspeter
1995.
Saddlepoint approximations for the probability of ruin in finite time.
Scandinavian Actuarial Journal,
Vol. 1995,
Issue. 2,
p.
169.
Jensen, Jens Ledet
1995.
Asymptotic expansions at work.
Scandinavian Actuarial Journal,
Vol. 1995,
Issue. 1,
p.
143.
Homble, Patrick
and
McCormick, William P.
1995.
Weak limit results for the extremes of a class of shot noise processes.
Journal of Applied Probability,
Vol. 32,
Issue. 03,
p.
707.
Preater, J.
1995.
A passage time for greedy‐coloring cycles.
Random Structures & Algorithms,
Vol. 6,
Issue. 1,
p.
105.
Routledge, Rick
and
Tsao, Min
1995.
Uniform validity of saddlepoint expansion on compact sets.
Canadian Journal of Statistics,
Vol. 23,
Issue. 4,
p.
425.
Reid, N.
1996.
Likelihood and higher‐order approximations to tail areas: A review and annotated bibliography.
Canadian Journal of Statistics,
Vol. 24,
Issue. 2,
p.
141.

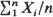 of
of 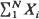 , where
, where 