Article contents
The size of a Markovian SIR epidemic given only removal data
Published online by Cambridge University Press: 21 March 2023
Abstract
During an epidemic outbreak, typically only partial information about the outbreak is known. A common scenario is that the infection times of individuals are unknown, but individuals, on displaying symptoms, are identified as infectious and removed from the population. We study the distribution of the number of infectives given only the times of removals in a Markovian susceptible–infectious–removed (SIR) epidemic. Primary interest is in the initial stages of the epidemic process, where a branching (birth–death) process approximation is applicable. We show that the number of individuals alive in a time-inhomogeneous birth–death process at time 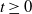 $t \geq 0$, given only death times up to and including time t, is a mixture of negative binomial distributions, with the number of mixing components depending on the total number of deaths, and the mixing weights depending upon the inter-arrival times of the deaths. We further consider the extension to the case where some deaths are unobserved. We also discuss the application of the results to control measures and statistical inference.
$t \geq 0$, given only death times up to and including time t, is a mixture of negative binomial distributions, with the number of mixing components depending on the total number of deaths, and the mixing weights depending upon the inter-arrival times of the deaths. We further consider the extension to the case where some deaths are unobserved. We also discuss the application of the results to control measures and statistical inference.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 2
- Cited by


