No CrossRef data available.
Article contents
Scaling limits for a random boxes model
Published online by Cambridge University Press: 03 September 2019
Abstract
We consider random rectangles in 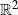 $\mathbb{R}^2$ that are distributed according to a Poisson random measure, i.e. independently and uniformly scattered in the plane. The distributions of the length and the width of the rectangles are heavy tailed with different parameters. We investigate the scaling behaviour of the related random fields as the intensity of the random measure grows to infinity while the mean edge lengths tend to zero. We characterise the arising scaling regimes, identify the limiting random fields, and give statistical properties of these limits.
$\mathbb{R}^2$ that are distributed according to a Poisson random measure, i.e. independently and uniformly scattered in the plane. The distributions of the length and the width of the rectangles are heavy tailed with different parameters. We investigate the scaling behaviour of the related random fields as the intensity of the random measure grows to infinity while the mean edge lengths tend to zero. We characterise the arising scaling regimes, identify the limiting random fields, and give statistical properties of these limits.
Keywords
MSC classification
Primary:
60G60: Random fields
Information
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2019
References
Baccelli, F. and Biswas, A. (2015). On scaling limits of power law shot-noise fields. Stoch. Models 31, 187–207.CrossRefGoogle Scholar
Biermé, H. and Desolneux, A. (2016). On the perimeter of excursion sets of shot noise random fields. Ann. Prob. 44, 521–543.CrossRefGoogle Scholar
Biermé, H., Durieu, O. and Wang, Y. (2018). Generalized operator-scaling random ball model. ALEA 15, 1401–1429.CrossRefGoogle Scholar
Biermé, H., Estrade, A. and Kaj, I. (2010). Self-similar random fields and rescaled random balls models. J. Theoret. Prob. 23, 1110–1141.CrossRefGoogle Scholar
Breton, J.-C. and Dombry, C. (2009). Rescaled weighted random ball models and stable self-similar random fields. Stoch. Process. Appl. 119, 3633–3652.CrossRefGoogle Scholar
Breton, J.-C. and Dombry, C. (2011). Functional macroscopic behavior of weighted random ball model. ALEA 8, 177–196.Google Scholar
Breton, J.-C. and Gobard, R. (2015). Infinite dimensional functional convergences in random balls model. ESAIM Prob. Statist. 19, 782–793.CrossRefGoogle Scholar
Breton, J.-C., Clarenne, A. and Gobard, R. (2019). Macroscopic analysis of determinantal random balls. Bernoulli 25, 1568–1601.CrossRefGoogle Scholar
Bulinskiĭ, A. V. (1992). Central limit theorem for shot-noise fields. J. Soviet Math. 61, 1840–1845.CrossRefGoogle Scholar
Çağlar, M. (2015). A Poisson shot-noise process of pulses and its scaling limits. Commun. Stoch. Anal. 9, 503–527.Google Scholar
Dombry, C. (2012). Extremal shot noises, heavy tails and max-stable random fields. Extremes 15, 129–158.CrossRefGoogle Scholar
Fasen, V. (2010). Modeling network traffic by a cluster Poisson input process with heavy and light-tailed file sizes. Queueing Systems 66, 313–350.CrossRefGoogle Scholar
Faÿ, G., González-Arévalo, B., Mikosch, T. and Samorodnitsky, G. (2006). Modeling teletraffic arrivals by a Poisson cluster process. Queueing Systems 54, 121–140.CrossRefGoogle Scholar
Gobard, R. (2015). Random balls model with dependence. J. Math. Anal. Appl. 423, 1284–1310.CrossRefGoogle Scholar
Iksanov, A., Marynych, A. and Meiners, M. (2014). Limit theorems for renewal shot noise processes with eventually decreasing response functions. Stoch. Process. Appl. 124, 2132–2170.CrossRefGoogle Scholar
Kaj, I. (2005). Limiting fractal random processes in heavy-tailed systems. In Fractals in Engineering, Springer, London, pp. 199–217.CrossRefGoogle Scholar
Kaj, I. and Taqqu, M. S. (2008). Convergence to fractional Brownian motion and to the Telecom process: the integral representation approach. In In and Out of Equilibrium 2, Birkhäuser, Basel, pp. 383–427.CrossRefGoogle Scholar
Kaj, I., Leskelä, L., Norros, I. and Schmidt, V. (2007). Scaling limits for random fields with long-range dependence. Ann. Prob. 35, 528–550.CrossRefGoogle Scholar
Kallenberg, O. (2002). Foundations of Modern Probability, 2nd edn. Springer, New York.CrossRefGoogle Scholar
Klüppelberg, C. and Kühn, C. (2004). Fractional Brownian motion as a weak limit of Poisson shot noise processes–with applications to finance. Stoch. Process. Appl. 113, 333–351.CrossRefGoogle Scholar
Klüppelberg, C., Mikosch, T. and Schärf, A. (2003). Regular variation in the mean and stable limits for Poisson shot noise. Bernoulli 9, 467–496.CrossRefGoogle Scholar
Lane, J. A. (1984). The central limit theorem for the Poisson shot-noise process. J. Appl. Prob. 21, 287–301.CrossRefGoogle Scholar
Lifshits, M. (2014). Random Processes by Example. World Scientific, Hackensack, NJ.CrossRefGoogle Scholar
Pang, G. and Zhou, Y. (2018). Functional limit theorems for a new class of non-stationary shot noise processes. Stoch. Process. Appl. 128, 505–544.CrossRefGoogle Scholar
Pilipauskaitė, V. and Surgailis, D. (2016). Anisotropic scaling of the random grain model with application to network traffic. J. Appl. Prob. 53, 857–879.CrossRefGoogle Scholar
Samorodnitsky, G. and Taqqu, M. S. (2000). Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance. Chapman & Hall, New York.Google Scholar

