Published online by Cambridge University Press: 01 July 2016
Point-process and other techniques are used to make a comprehensive investigation of the almost-sure behaviour of partial maxima 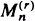 (the rth largest among a sample of n i.i.d. random variables), partial record values
(the rth largest among a sample of n i.i.d. random variables), partial record values 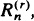 and differences and quotients involving them. In particular, we obtain characterizations of such asymptotic properties as
and differences and quotients involving them. In particular, we obtain characterizations of such asymptotic properties as 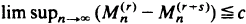 a.s. for some finite constant c, or
a.s. for some finite constant c, or 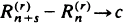 a.s. for some constant c in [0,∞], which tell us, in various ways, how quickly the sequences increase. These characterizations take the form of integral conditions on the tail of F, which furthermore characterize such properties as stability and relative stability of the sequence of maxima. We also develop their relation to the large-sample behaviour of trimmed sums, and discuss some statistical applications.
a.s. for some constant c in [0,∞], which tell us, in various ways, how quickly the sequences increase. These characterizations take the form of integral conditions on the tail of F, which furthermore characterize such properties as stability and relative stability of the sequence of maxima. We also develop their relation to the large-sample behaviour of trimmed sums, and discuss some statistical applications.
Present address: School of Mathematical Sciences, University of Sussex, Brighton, BN1 6HE, UK.