Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Van Dijk, Nico M.
1988.
Perturbation theory for unbounded Markov reward processes with applications to queueing.
Advances in Applied Probability,
Vol. 20,
Issue. 01,
p.
99.
Van Dijk, Nico M.
1990.
Analytic error bounds for approximations of queueing networks with an application to alternate routing.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 31,
Issue. 3,
p.
241.
Van Dijk, Nico M.
1991.
On truncations and perturbations of Markov decision problems with an application to queueing network overflow control.
Annals of Operations Research,
Vol. 29,
Issue. 1,
p.
515.
van Dijk, Nico M
1991.
Transient error bound analysis for continuous-time Markov reward structures.
Performance Evaluation,
Vol. 13,
Issue. 3,
p.
147.
Abbad, M.
and
Filar, J.A.
1991.
Perturbation theory for semi-Markov control problems.
p.
489.
Bielecki, Tomasz R.
and
Filar, Jerzy A.
1991.
Singularly perturbed Markov control problem: Limiting average cost.
Annals of Operations Research,
Vol. 28,
Issue. 1,
p.
153.
Abbad, M.
and
Filar, J.A.
1991.
Aggregation-disaggregation algorithm for epsilon /sup 2/-singularly perturbed limiting average Markov control problems.
p.
465.
Liu, Zhen
and
Nain, Philippe
1991.
Sensitivity results in open, closed and mixed product form queueing networks.
Performance Evaluation,
Vol. 13,
Issue. 4,
p.
237.
Grassi, Vincenzo
and
Donatiello, Lorenzo
1992.
Sensitivity analysis of performability.
Performance Evaluation,
Vol. 14,
Issue. 3-4,
p.
227.
Abbad, M.
and
Filar, J.A.
1992.
Perturbation and stability theory for Markov control problems.
IEEE Transactions on Automatic Control,
Vol. 37,
Issue. 9,
p.
1415.
Ramesh, A. V.
and
Trivedi, Kishor
1993.
On the sensitivity of transient solutions of Markov models.
p.
122.
Haverkort, Boudewijn R.
1993.
Approximate performability and dependability analysis using generalized stochastic Petri nets.
Performance Evaluation,
Vol. 18,
Issue. 1,
p.
61.
Ramesh, A. V.
and
Trivedi, Kishor
1993.
On the sensitivity of transient solutions of Markov models.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 21,
Issue. 1,
p.
122.
Kovalenko, Igor N.
1994.
Rare events in queueing systems?A survey.
Queueing Systems,
Vol. 16-16,
Issue. 1-2,
p.
1.
Burnetas, Apostolos N.
and
Katehakis, Michael N.
1995.
Computing Optimal Policies for Markovian Decision Processes Using Simulation.
Probability in the Engineering and Informational Sciences,
Vol. 9,
Issue. 4,
p.
525.
Abbad, Mohammed
and
Jerzy, A. Filar
1995.
Techniques in Discrete-Time Stochastic Control Systems.
Vol. 73,
Issue. ,
p.
257.
van Dijk, Nico M.
and
Sladký, Karel
1996.
Operations Research Proceedings 1995.
Vol. 1995,
Issue. ,
p.
96.
Van Dijk, Nico M.
1996.
A Note on Time Monotonicity for Performability Models.
Probability in the Engineering and Informational Sciences,
Vol. 10,
Issue. 2,
p.
299.
Burnetas, Apostolos N.
and
Katehakis, Michael N.
1997.
On confidence intervals from simulation of finite Markov chains.
Mathematical Methods of Operations Research,
Vol. 46,
Issue. 2,
p.
241.
Gordienko, Evgueni
Montes-De-Oca, Ra�l
and
Minj�rez-Sosa, Adolfo
1997.
Approximation of average cost optimal policies for general Markov decision processes with unbounded costs.
Mathematical Methods of Operations Research,
Vol. 45,
Issue. 2,
p.
245.

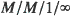 ). Extensions to Markov decision processes and other settings are discussed.
). Extensions to Markov decision processes and other settings are discussed.