Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dufresne, Daniel
1998.
Algebraic Properties of Beta and Gamma Distributions, and Applications.
Advances in Applied Mathematics,
Vol. 20,
Issue. 3,
p.
285.
Grübel, Rudolf
1998.
Hoare's Selection Algorithm: A Markov Chain Approach.
Journal of Applied Probability,
Vol. 35,
Issue. 01,
p.
36.
Grübel, Rudolf
and
Pitts, Susan M
2000.
Statistical Aspects of Perpetuities.
Journal of Multivariate Analysis,
Vol. 75,
Issue. 1,
p.
143.
Embrechts, Paul
and
Walk, Harro
2000.
Recursive estimation of distributional fix-points.
Journal of Applied Probability,
Vol. 37,
Issue. 1,
p.
73.
Embrechts, Paul
and
Walk, Harro
2000.
Recursive estimation of distributional fix-points.
Journal of Applied Probability,
Vol. 37,
Issue. 01,
p.
73.
Devroye, Luc
2001.
Simulating Perpetuities.
Methodology And Computing In Applied Probability,
Vol. 3,
Issue. 1,
p.
97.
Grübel, Rudolf
and
Reimers, Anke
2001.
On the total time spent in records by a discrete uniform sequence.
Journal of Applied Probability,
Vol. 38,
Issue. 03,
p.
768.
Grübel, Rudolf
and
Reimers, Anke
2001.
On the total time spent in records by a discrete uniform sequence.
Journal of Applied Probability,
Vol. 38,
Issue. 3,
p.
768.
Devroye, Luc
and
Neininger, Ralph
2002.
Density approximation and exact simulation of random variables that are solutions of fixed-point equations.
Advances in Applied Probability,
Vol. 34,
Issue. 2,
p.
441.
Penrose, Mathew D.
and
Wade, Andrew R.
2004.
Random minimal directed spanning trees and Dickman-type distributions.
Advances in Applied Probability,
Vol. 36,
Issue. 3,
p.
691.
Konstantinides, Dimitrios G.
and
Mikosch, Thomas
2005.
Large deviations and ruin probabilities for solutions to stochastic recurrence equations with heavy-tailed innovations.
The Annals of Probability,
Vol. 33,
Issue. 5,
Maulik, Krishanu
and
Zwart, Bert
2006.
Tail asymptotics for exponential functionals of Lévy processes.
Stochastic Processes and their Applications,
Vol. 116,
Issue. 2,
p.
156.
Iksanov, A. M.
and
Rösler, U.
2006.
Some moment results about the limit of a martingale related to the supercritical branching random walk and perpetuities.
Ukrainian Mathematical Journal,
Vol. 58,
Issue. 4,
p.
505.
Devroye, Luc
2006.
Simulation.
Vol. 13,
Issue. ,
p.
83.
Roitershtein, Alexander
2007.
One-dimensional linear recursions with Markov-dependent coefficients.
The Annals of Applied Probability,
Vol. 17,
Issue. 2,
Klivečka, A.
and
Surgailis, D.
2007.
Garch(1,1) process can have arbitrarily heavy power tails.
Lithuanian Mathematical Journal,
Vol. 47,
Issue. 2,
p.
164.
Denisov, Denis
and
Zwart, Bert
2007.
On a Theorem of Breiman and a Class of Random Difference Equations.
Journal of Applied Probability,
Vol. 44,
Issue. 04,
p.
1031.
Knape, Margarete
and
Neininger, Ralph
2008.
Approximating Perpetuities.
Methodology and Computing in Applied Probability,
Vol. 10,
Issue. 4,
p.
507.
Ambroževičiūtė, D.
and
Klivečka, A.
2008.
On the tvGARCH(1,1) model: Existence, CLT, and tail index.
Lithuanian Mathematical Journal,
Vol. 48,
Issue. 1,
p.
1.
Bobecka, Konstancja
and
Wesołowski, Jacek
2008.
Kshirsagar–Tan independence property of beta matrices and related characterizations.
Bernoulli,
Vol. 14,
Issue. 3,

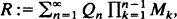 where
where 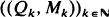 is an independent, identically distributed sequence with
is an independent, identically distributed sequence with 