Article contents
Limit theorems for critical branching processes in a finite-state-space Markovian environment
Published online by Cambridge University Press: 01 March 2022
Abstract
Let 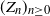 $(Z_n)_{n\geq 0}$ be a critical branching process in a random environment defined by a Markov chain
$(Z_n)_{n\geq 0}$ be a critical branching process in a random environment defined by a Markov chain 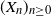 $(X_n)_{n\geq 0}$ with values in a finite state space
$(X_n)_{n\geq 0}$ with values in a finite state space 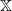 $\mathbb{X}$. Let
$\mathbb{X}$. Let 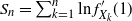 $ S_n = \sum_{k=1}^n \ln f_{X_k}^{\prime}(1)$ be the Markov walk associated to
$ S_n = \sum_{k=1}^n \ln f_{X_k}^{\prime}(1)$ be the Markov walk associated to 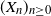 $(X_n)_{n\geq 0}$, where
$(X_n)_{n\geq 0}$, where 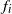 $f_i$ is the offspring generating function when the environment is
$f_i$ is the offspring generating function when the environment is 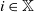 $i \in \mathbb{X}$. Conditioned on the event
$i \in \mathbb{X}$. Conditioned on the event  $\{ Z_n>0\}$, we show the nondegeneracy of the limit law of the normalized number of particles
$\{ Z_n>0\}$, we show the nondegeneracy of the limit law of the normalized number of particles 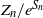 ${Z_n}/{e^{S_n}}$ and determine the limit of the law of
${Z_n}/{e^{S_n}}$ and determine the limit of the law of 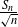 $\frac{S_n}{\sqrt{n}} $ jointly with
$\frac{S_n}{\sqrt{n}} $ jointly with 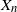 $X_n$. Based on these results we establish a Yaglom-type theorem which specifies the limit of the joint law of
$X_n$. Based on these results we establish a Yaglom-type theorem which specifies the limit of the joint law of 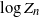 $ \log Z_n$ and
$ \log Z_n$ and 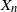 $X_n$ given
$X_n$ given 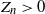 $Z_n>0$.
$Z_n>0$.
Keywords
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 1
- Cited by


