Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Karlin, Samuel
and
Brendel, Volker
1992.
Chance and Statistical Significance in Protein and DNA Sequence Analysis.
Science,
Vol. 257,
Issue. 5066,
p.
39.
Louchard, Guy
and
Szpankowski, Wojciech
1993.
Combinatorial Pattern Matching.
Vol. 684,
Issue. ,
p.
152.
Dembo, Amir
and
Karlin, Samuel
1993.
Central limit theorems of partial sums for large segmental values.
Stochastic Processes and their Applications,
Vol. 45,
Issue. 2,
p.
259.
Reich, Jens G.
1994.
Computational Methods in Genome Research.
p.
137.
Zajic, Tim
1995.
Large exceedences for uniformly recurrent Markov-additive processes and strong-mixing stationary processes.
Journal of Applied Probability,
Vol. 32,
Issue. 03,
p.
679.
Brendel, Volker
1996.
Advances in Computational Biology.
p.
121.
Collamore, Jeffrey F.
1996.
Hitting probabilities and large deviations.
The Annals of Probability,
Vol. 24,
Issue. 4,
States, David J.
1997.
Calculating the secrets of life.
Computers & Chemistry,
Vol. 21,
Issue. 4,
p.
279.
Fuh, C. D.
1997.
Corrected Diffusion Approximations for Ruin Probabilities in a Markov Random Walk.
Advances in Applied Probability,
Vol. 29,
Issue. 03,
p.
695.
Xiong, Momiao
and
Waterman, Michael S.
1997.
A Phase Transition for the Minimum Free Energy of Secondary Structures of a Random RNA.
Advances in Applied Mathematics,
Vol. 18,
Issue. 2,
p.
111.
Braun, Jerome V.
and
Müller, Hans-Georg
1998.
Statistical methods for DNA sequence segmentation.
Statistical Science,
Vol. 13,
Issue. 2,
Daudin, Jean-Jacques
and
Mercier, Sabine
1999.
Distribution exacte du score local d'une suite de variables indépendentes et identiquement distribuées.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 329,
Issue. 9,
p.
815.
Ewens, W. J.
1999.
Statistics in Genetics.
Vol. 112,
Issue. ,
p.
147.
Lotov, V. I.
1999.
On hitting the high level by a random walk with delay at the origin.
Siberian Mathematical Journal,
Vol. 40,
Issue. 6,
p.
1079.
Bundschuh, R.
and
Hwa, T.
1999.
An analytic study of the phase transition line in local sequence alignment with gaps.
p.
70.
MOTT, RICHARD
and
TRIBE, ROGER
1999.
Approximate Statistics of Gapped Alignments.
Journal of Computational Biology,
Vol. 6,
Issue. 1,
p.
91.
Spouge, John L.
Marchler-Bauer, Aron
and
Bryant, Stephen
1999.
The combinatorics and extreme value statistics of protein threading.
Annals of Combinatorics,
Vol. 3,
Issue. 1,
p.
81.
Bundschuh, R.
and
Hwa, T.
2000.
An analytic study of the phase transition line in local sequence alignment with gaps.
Discrete Applied Mathematics,
Vol. 104,
Issue. 1-3,
p.
113.
Siegmund, David
and
Yakir, Benjamin
2000.
Approximate $p$-values for local sequence alignments.
The Annals of Statistics,
Vol. 28,
Issue. 3,
Mott, Richard
2000.
Accurate formula for P-values of gapped local sequence and profile alignments.
Journal of Molecular Biology,
Vol. 300,
Issue. 3,
p.
649.

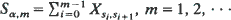 is determined by a realization
is determined by a realization 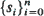 of states with s
of states with s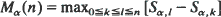 is derived. Computational methods with potential applications to the analysis of random Markov-dependent letter sequences (e.g. DNA and protein sequences) are presented.
is derived. Computational methods with potential applications to the analysis of random Markov-dependent letter sequences (e.g. DNA and protein sequences) are presented.