No CrossRef data available.
Article contents
Estimation of the correlation between relatives
Published online by Cambridge University Press: 01 July 2016
Extract
Suppose, to take a simple example, we have a set of sibships. Each individual (sib) has a certain measured character x. We wish to estimate the interclass (or sib–sib) correlation for this character. Our model is as follows. In sibship s the observed values x are supposed drawn from a distribution with (true) mean m s and variance v s . The sibships are drawn from a population of sibships, so that the m s have a mean M and variance B, and the v s have mean A. (We also suppose that the number n s of sibs in sibship s is independent of m s and v s .) The interclass correlation is then easily seen to be
ρ = B/(A + B).
The obvious way to proceed is to estimate A and B first, and then find ρ. Take a sample of k sibships. In sibship s the observed mean is 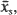 and the deviance (sum of squares of deviations) δs . Let n = σ n s = the total number of individuals in the sample, and δ = σ δs = the total deviance within sibships. Proceed iteratively as follows:
and the deviance (sum of squares of deviations) δs . Let n = σ n s = the total number of individuals in the sample, and δ = σ δs = the total deviance within sibships. Proceed iteratively as follows:
Information
- Type
- Symposium on Mathematical Genetics, London, 26–27 March 1979
- Information
- Copyright
- Copyright © Applied Probability Trust 1980

