Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kellerer, A. M.
1985.
Counting figures in planar random configurations.
Journal of Applied Probability,
Vol. 22,
Issue. 01,
p.
68.
Stoyan, D.
and
Hermann, H.
1986.
Some methods for statistical analysis of planar random tessellations.
Statistics,
Vol. 17,
Issue. 3,
p.
407.
Wieacker, John André
1986.
Intersections of random hypersurfaces and visibility.
Probability Theory and Related Fields,
Vol. 71,
Issue. 3,
p.
405.
Zähle, M.
1986.
Curvature measures and random sets II.
Probability Theory and Related Fields,
Vol. 71,
Issue. 1,
p.
37.
Cressie, Noel
and
Laslett, G. M.
1987.
Random Set Theory and Problems of Modeling.
SIAM Review,
Vol. 29,
Issue. 4,
p.
557.
Weil, Wolfgang
1987.
Stochastic and Integral Geometry.
p.
103.
Well, Wolfgang
1987.
Point processes of cylinders, particles and flats.
Acta Applicandae Mathematicae,
Vol. 9,
Issue. 1-2,
p.
103.
Weil, Wolfgang
1988.
Expectation formulas and isoperimetric properties for non‐isotropic Boolean models.
Journal of Microscopy,
Vol. 151,
Issue. 3,
p.
235.
Weil, Wolfgang
1990.
Iterations of translative integral formulae and non-isotropic Poisson processes of particles.
Mathematische Zeitschrift,
Vol. 205,
Issue. 1,
p.
531.
Schmitt, Michel
1991.
Estimation of the density in a stationary Boolean model.
Journal of Applied Probability,
Vol. 28,
Issue. 03,
p.
702.
Betke, Ulrich
and
Weil, Wolfgang
1991.
Isoperimetric inequalities for the mixed area of plane convex sets.
Archiv der Mathematik,
Vol. 57,
Issue. 5,
p.
501.
Heinrich, L.
1992.
On existence and mixing properties of germ-grain models.
Statistics,
Vol. 23,
Issue. 3,
p.
271.
WEIL, Wolfgang
and
WIEACKER, John A.
1993.
Handbook of Convex Geometry.
p.
1391.
1993.
Statistics for Spatial Data.
p.
803.
Molchanov, Ilya
and
Stoyan, Dietrich
1994.
Asymptotic properties of estimators for parameters of the Boolean model.
Advances in Applied Probability,
Vol. 26,
Issue. 02,
p.
301.
Hiorns, Robert
and
Prum, Bernard
1994.
First European Congress of Mathematics.
p.
515.
Molchanov, Ilya S.
1995.
Statistics of the Boolean model: from the estimation of means to the estimation of distributions.
Advances in Applied Probability,
Vol. 27,
Issue. 1,
p.
63.
Dougherty, Edward R.
and
Handley, John C.
1995.
Recursive maximum-likelihood estimation in the one-dimensional discrete Boolean random set model.
Signal Processing,
Vol. 43,
Issue. 1,
p.
1.
Weil, Wolfgang
1995.
The Estimation of mean shape and mean particle number in overlapping particle systems in the plane.
Advances in Applied Probability,
Vol. 27,
Issue. 1,
p.
102.
Fallert, Hermann
1996.
Quermaßdichten für Punktprozesse konvexer Körper und Boolesche Modelle.
Mathematische Nachrichten,
Vol. 181,
Issue. 1,
p.
165.

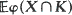 are derived when
are derived when 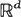 . In particular, for the quermassintegrals and motioninvariant
. In particular, for the quermassintegrals and motioninvariant 