Article contents
Convergence in mean of some characteristics of the convex hull
Published online by Cambridge University Press: 01 July 2016
Abstract
A sequence X n , 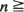 1 of independent and identically distributed random vectors is considered. Under a condition of regular variation, the number of vertices of the convex hull of {X 1, …, X n} converges in distribution to the number of vertices of the convex hull of a certain Poisson point process. In this paper, it is proved without sharpening the conditions that the expectation of this number also converges; expressions are found for its limit, generalizing results of Davis et al. (1987). We also present some results concerning other quantities of interest, such as area and perimeter of the convex hull and the probability that a given point belongs to the convex hull.
1 of independent and identically distributed random vectors is considered. Under a condition of regular variation, the number of vertices of the convex hull of {X 1, …, X n} converges in distribution to the number of vertices of the convex hull of a certain Poisson point process. In this paper, it is proved without sharpening the conditions that the expectation of this number also converges; expressions are found for its limit, generalizing results of Davis et al. (1987). We also present some results concerning other quantities of interest, such as area and perimeter of the convex hull and the probability that a given point belongs to the convex hull.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 1989
Footnotes
This study was funded by the Netherlands Organization for the Advancement of Pure Research (N.W.O.).
References
- 9
- Cited by

