Article contents
Characterization of the conditional stationary distribution in Markov chains via systems of linear inequalities
Published online by Cambridge University Press: 03 December 2020
Abstract
This paper considers ergodic, continuous-time Markov chains 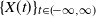 $\{X(t)\}_{t \in (\!-\infty,\infty)}$ on
$\{X(t)\}_{t \in (\!-\infty,\infty)}$ on 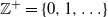 $\mathbb{Z}^+=\{0,1,\ldots\}$. For an arbitrarily fixed
$\mathbb{Z}^+=\{0,1,\ldots\}$. For an arbitrarily fixed 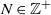 $N \in \mathbb{Z}^+$, we study the conditional stationary distribution
$N \in \mathbb{Z}^+$, we study the conditional stationary distribution 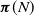 $\boldsymbol{\pi}(N)$ given the Markov chain being in
$\boldsymbol{\pi}(N)$ given the Markov chain being in 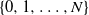 $\{0,1,\ldots,N\}$. We first characterize
$\{0,1,\ldots,N\}$. We first characterize 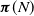 $\boldsymbol{\pi}(N)$ via systems of linear inequalities and identify simplices that contain
$\boldsymbol{\pi}(N)$ via systems of linear inequalities and identify simplices that contain 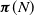 $\boldsymbol{\pi}(N)$, by examining the
$\boldsymbol{\pi}(N)$, by examining the 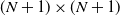 $(N+1) \times (N+1)$ northwest corner block of the infinitesimal generator
$(N+1) \times (N+1)$ northwest corner block of the infinitesimal generator 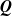 $\textbf{\textit{Q}}$ and the subset of the first
$\textbf{\textit{Q}}$ and the subset of the first 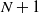 $N+1$ states whose members are directly reachable from at least one state in
$N+1$ states whose members are directly reachable from at least one state in 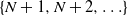 $\{N+1,N+2,\ldots\}$. These results are closely related to the augmented truncation approximation (ATA), and we provide some practical implications for the ATA. Next we consider an extension of the above results, using the
$\{N+1,N+2,\ldots\}$. These results are closely related to the augmented truncation approximation (ATA), and we provide some practical implications for the ATA. Next we consider an extension of the above results, using the 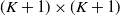 $(K+1) \times (K+1)$ (
$(K+1) \times (K+1)$ (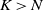 $K > N$) northwest corner block of
$K > N$) northwest corner block of 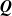 $\textbf{\textit{Q}}$ and the subset of the first
$\textbf{\textit{Q}}$ and the subset of the first 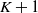 $K+1$ states whose members are directly reachable from at least one state in
$K+1$ states whose members are directly reachable from at least one state in 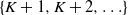 $\{K+1,K+2,\ldots\}$. Furthermore, we introduce new state transition structures called (K, N)-skip-free sets, using which we obtain the minimum convex polytope that contains
$\{K+1,K+2,\ldots\}$. Furthermore, we introduce new state transition structures called (K, N)-skip-free sets, using which we obtain the minimum convex polytope that contains 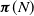 $\boldsymbol{\pi}(N)$.
$\boldsymbol{\pi}(N)$.
Keywords
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 2
- Cited by


