Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mardia, K. V.
1981.
Statistical Distributions in Scientific Work.
p.
1.
Small, Christopher
1982.
Random uniform triangles and the alignment problem.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 91,
Issue. 2,
p.
315.
Hall, Glen Richard
1982.
Acute triangles in the n-ball.
Journal of Applied Probability,
Vol. 19,
Issue. 03,
p.
712.
Zuiderwijk, E. J.
1982.
Alignment of randomly distributed objects.
Nature,
Vol. 295,
Issue. 5850,
p.
577.
Hanisch, K. -H.
1983.
Reduction of n-th moment measures and the special case of the third moment measure of stationary and isotropic planar point processes.
Series Statistics,
Vol. 14,
Issue. 3,
p.
421.
Small, Christopher G.
1983.
Characterization of distributions from maximal invariant statistics.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 63,
Issue. 4,
p.
517.
Weber, N. C.
1983.
Central limit theorems for a class of symmetric statistics.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 94,
Issue. 2,
p.
307.
Bhavsar, S. P.
and
Barrow, J. D.
1984.
Clusters and Groups of Galaxies.
Vol. 111,
Issue. ,
p.
415.
Clifford, Peter
and
Green, N. J. B.
1985.
Distances in Gaussian point sets.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 97,
Issue. 3,
p.
515.
Bradley, Richard
and
Small, Christopher
1985.
Looking for circular structures in post hole distributions: Quantitative analysis of two settlements from bronze age England.
Journal of Archaeological Science,
Vol. 12,
Issue. 4,
p.
285.
Kendall, David G.
1985.
A Celebration of Statistics.
p.
393.
Kendall, D. G.
1985.
Exact distributions for shapes of random triangles in convex sets.
Advances in Applied Probability,
Vol. 17,
Issue. 02,
p.
308.
Zhu, Xing-fen
1986.
On the alignment of quasars.
Chinese Astronomy and Astrophysics,
Vol. 10,
Issue. 2,
p.
94.
Kendall, David G.
1986.
The Craft of Probabilistic Modelling.
Vol. 1,
Issue. ,
p.
3.
Kendall, David G.
1987.
Further Developments and Applications of the Statistical Theory of Shape.
Theory of Probability & Its Applications,
Vol. 31,
Issue. 3,
p.
407.
Clifford, Peter
Green, N. J. B.
and
Pilling, M. J.
1987.
Statistical Models of Chemical Kinetics in Liquids.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 49,
Issue. 3,
p.
266.
Gosset, E.
Surdej, J.
and
Swings, J.P.
1987.
Is There an Alignment of Quasars Near NGC 520?.
Symposium - International Astronomical Union,
Vol. 124,
Issue. ,
p.
499.
Csörgő, Miklós
and
Horváth, Lajos
1987.
Asymptotic distributions of pontograms.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 101,
Issue. 1,
p.
131.
Gosset, E.
Surdej, J.
and
Swings, J. P.
1987.
Observational Cosmology.
p.
499.
Le, Hui-Lin
1987.
Explicit formulae for polygonally generated shape-densities in the basic tile.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 101,
Issue. 2,
p.
313.
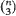 resulting triads form triangles with largest angle ≧ π – ∊. The main object of the paper is to obtain asymptotic formulae for
resulting triads form triangles with largest angle ≧ π – ∊. The main object of the paper is to obtain asymptotic formulae for 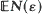 and Var (N(∊)) when ∊ ↓ 0, and to solve the associated data-analytic problem of testing whether an empirical set of n points should be considered to contain too many such ∊-blunt triads in the situation where the generating mechanism is unknown and where all that can be said about the tolerance ∊ is that it must be allowed to take values anywhere in a given interval (T 0, T 1) (0 < T 0 < T 1). This problem is solved by the introduction of a plot to be called the pontogram and by the introduction of simulation-based significance tests constructed by random lateral perturbations of the data.
and Var (N(∊)) when ∊ ↓ 0, and to solve the associated data-analytic problem of testing whether an empirical set of n points should be considered to contain too many such ∊-blunt triads in the situation where the generating mechanism is unknown and where all that can be said about the tolerance ∊ is that it must be allowed to take values anywhere in a given interval (T 0, T 1) (0 < T 0 < T 1). This problem is solved by the introduction of a plot to be called the pontogram and by the introduction of simulation-based significance tests constructed by random lateral perturbations of the data.
