Conditions are derived under which a probability measure on the Borel subsets of [0, ∞) is a stationary distribution for the content {Xt } of an infinite dam whose cumulative input {At } is a pure-jump Lévy process and whose release rate is a non-decreasing continuous function r(·) of the content. 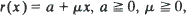The conditions are used to find stationary distributions in a number of special cases, in particular when and when r(x) = x α and {A t } is stable with index β ∊ (0, 1). In general if EAt , < ∞ and r(0 +) > 0 it is shown that the condition sup r(x)>EA 1 is necessary and sufficient for a stationary distribution to exist, a stationary distribution being found explicitly when the conditions are satisfied. If sup r(x)>EA 1 it is shown that there is at most one stationary distribution and that if there is one then it is the limiting distribution of {Xt } as t → ∞. For {At } stable with index β and r(x) = x α , α + β = 1, we show also that 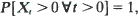complementing results of Brockwell and Chung for the zero-set of {Xt } in the cases α + β < 1 and α + β > 1. We conclude with a brief treatment of the finite dam, regarded as a limiting case of infinite dams with suitably chosen release functions.