Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Frees, Edward W.
1986.
Nonparametric Estimation of the Probability of Ruin.
ASTIN Bulletin,
Vol. 16,
Issue. S1,
p.
S81.
Janson, Svante
1987.
Annals of Discrete Mathematics (33), Proceedings of the International Conference on Finite Geometries and Combinatorial Structures.
Vol. 144,
Issue. ,
p.
91.
Yao, Qiwei
1988.
Repeated likelihood ratio test for the variance of normal distribution with unknown mean.
Acta Mathematicae Applicatae Sinica,
Vol. 4,
Issue. 4,
p.
296.
Woodroofe, Michael
1988.
Asymptotic expansions for first passage times.
Stochastic Processes and their Applications,
Vol. 28,
Issue. 2,
p.
301.
Walk, H.
1989.
Nonlinear renewal theory under growth conditions.
Stochastic Processes and their Applications,
Vol. 32,
Issue. 2,
p.
289.
Kuczek, Thomas
and
Crank, Keith N.
1991.
A large-deviation result for regenerative processes.
Journal of Theoretical Probability,
Vol. 4,
Issue. 3,
p.
551.
Wang, Mei
1992.
A local limit theorem for perturbed random walks.
Statistics & Probability Letters,
Vol. 15,
Issue. 2,
p.
109.
Allan, Gut
1992.
First passage times for perturbed random walks.
Sequential Analysis,
Vol. 11,
Issue. 2,
p.
149.
Lehtonen, Tapani
and
Nyrhinen, Harri
1992.
On asymptotically efficient simulation of ruin probabilities in a Markovian environment.
Scandinavian Actuarial Journal,
Vol. 1992,
Issue. 1,
p.
60.
Kroese, D.P.
and
Kallenberg, W.C.M.
1992.
Second-order asymptotics in level crossing for differences of renewal processes.
Stochastic Processes and their Applications,
Vol. 40,
Issue. 2,
p.
309.
Lehtonen, T.
and
Nyrhinen, H.
1992.
Simulating level-crossing probabilities by importance sampling.
Advances in Applied Probability,
Vol. 24,
Issue. 4,
p.
858.
Su, Yeongtzay
1993.
Limit theorems for first-passage times in non–linear markov renewal theory.
Sequential Analysis,
Vol. 12,
Issue. 3-4,
p.
235.
Ragimov, F. G.
1993.
Asymptotic Expansion for the Distribution of Nonlinear Boundary Crossing Time.
Theory of Probability & Its Applications,
Vol. 37,
Issue. 3,
p.
560.
Xiong, Xiaoping
1995.
A Class of Sequential Conditional Probability Ratio Tests.
Journal of the American Statistical Association,
Vol. 90,
Issue. 432,
p.
1463.
Nyrhinen, Harri
1995.
On the typical level crossing time and path.
Stochastic Processes and their Applications,
Vol. 58,
Issue. 1,
p.
121.
Wang, Mei
1996.
Limit theorems on occupation times for perturbed random walks.
Sequential Analysis,
Vol. 15,
Issue. 2-3,
p.
103.
Collamore, Jeffrey F.
1996.
Hitting probabilities and large deviations.
The Annals of Probability,
Vol. 24,
Issue. 4,
Fuh, C. D.
1997.
Corrected Diffusion Approximations for Ruin Probabilities in a Markov Random Walk.
Advances in Applied Probability,
Vol. 29,
Issue. 3,
p.
695.
Yeongtzay, Su
and
Chitshung, Wang
1998.
Nonlinear renewal theory for lattice markov random walk.
Sequential Analysis,
Vol. 17,
Issue. 3-4,
p.
267.
Nyrhinen, Harri
1998.
Rough descriptions of ruin for a general class of surplus processes.
Advances in Applied Probability,
Vol. 30,
Issue. 4,
p.
1008.

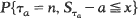 is obtained, where
is obtained, where 