Article contents
Clustering of Bursts of Openings in Markov and Semi-Markov Models of Single Channel Gating
Published online by Cambridge University Press: 01 July 2016
Abstract
The gating mechanism of a single ion channel is usually modelled by a continuous-time Markov chain with a finite state space. The state space is partitioned into two classes, termed ‘open’ and ‘closed’, and it is possible to observe only which class the process is in. In many experiments channel openings occur in bursts. This can be modelled by partitioning the closed states further into ‘short-lived’ and ‘long-lived’ closed states, and defining a burst of openings to be a succession of open sojourns separated by closed sojourns that are entirely within the short-lived closed states. There is also evidence that bursts of openings are themselves grouped together into clusters. This clustering of bursts can be described by the ratio of the variance Var (N(t)) to the mean 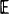 [N(t)] of the number of bursts of openings commencing in (0, t]. In this paper two methods of determining Var (N(t))/
[N(t)] of the number of bursts of openings commencing in (0, t]. In this paper two methods of determining Var (N(t))/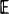 [N(t)] and limt→∝ Var (N(t))/
[N(t)] and limt→∝ Var (N(t))/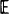 [N(t)] are developed, the first via an embedded Markov renewal process and the second via an augmented continuous-time Markov chain. The theory is illustrated by a numerical study of a molecular stochastic model of the nicotinic acetylcholine receptor. Extensions to semi-Markov models of ion channel gating and the incorporation of time interval omission are briefly discussed.
[N(t)] are developed, the first via an embedded Markov renewal process and the second via an augmented continuous-time Markov chain. The theory is illustrated by a numerical study of a molecular stochastic model of the nicotinic acetylcholine receptor. Extensions to semi-Markov models of ion channel gating and the incorporation of time interval omission are briefly discussed.
Keywords
MSC classification
Information
- Type
- General Applied Probability
- Information
- Copyright
- Copyright © Applied Probability Trust 1997
References
- 8
- Cited by

