Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Masuda, Yasushi
1988.
First passage times of birth-death processes and simple random walks.
Stochastic Processes and their Applications,
Vol. 29,
Issue. 1,
p.
51.
Wenocur, Michael L.
1989.
Approximating probability densities on the positive half-line.
Queueing Systems,
Vol. 4,
Issue. 2,
p.
115.
Harris, Carl M.
MARCHAL, WILLIAM G.
and
BOTTA, ROBERT F.
1992.
A note on generalized hyperexponential distributions.
Communications in Statistics. Stochastic Models,
Vol. 8,
Issue. 1,
p.
179.
Di Crescenzo, Antonio
1998.
First-passage-time densities and avoiding probabilities for birth-and-death processes with symmetric sample paths.
Journal of Applied Probability,
Vol. 35,
Issue. 02,
p.
383.
Brown, Mark
1999.
Interlacing Eigenvalues in Time Reversible Markov Chains.
Mathematics of Operations Research,
Vol. 24,
Issue. 4,
p.
847.
Commault, Christian
and
Mocanu, Stéphane
2003.
Phase-type distributions and representations: Some results and open problems for system theory.
International Journal of Control,
Vol. 76,
Issue. 6,
p.
566.
Sumita, Ushio
Gotoh, Jun-ya
and
Jin, Hui
2006.
NUMERICAL EXPLORATION OF DYNAMIC BEHAVIOR OF ORNSTEIN-UHLENBECK PROCESSES VIA EHRENFEST PROCESS APPROXIMATION(<Special Issue>Advanced Planning and Scheduling for Supply Chain Management).
Journal of the Operations Research Society of Japan,
Vol. 49,
Issue. 3,
p.
256.
Bean, Nigel G.
Fackrell, Mark
and
Taylor, Peter
2008.
Characterization of Matrix-Exponential Distributions.
Stochastic Models,
Vol. 24,
Issue. 3,
p.
339.
Fackrell, Mark
2009.
An alternative characterization for matrix exponential distributions.
Advances in Applied Probability,
Vol. 41,
Issue. 04,
p.
1005.
Dufresne, Daniel
2010.
G distributions and the beta-gamma algebra.
Electronic Journal of Probability,
Vol. 15,
Issue. none,
Avram, F.
Chedom, D.F.
and
Horváth, A.
2011.
On moments based Padé approximations of ruin probabilities.
Journal of Computational and Applied Mathematics,
Vol. 235,
Issue. 10,
p.
3215.
Fackrell, Mark
2012.
A semi-infinite programming approach to identifying matrix-exponential distributions.
International Journal of Systems Science,
Vol. 43,
Issue. 9,
p.
1623.
Reinecke, Philipp
and
Telek, Miklós
2014.
Does a given vector–matrix pair correspond to a PH distribution?.
Performance Evaluation,
Vol. 81,
Issue. ,
p.
40.
Chiu, Sung Nok
and
Yin, Chuancun
2014.
On the complete monotonicity of the compound geometric convolution with applications in risk theory.
Scandinavian Actuarial Journal,
Vol. 2014,
Issue. 2,
p.
116.
Wu, Lan
and
Zhou, Jiang
2016.
Occupation times of hyper-exponential jump diffusion processes with application to price step options.
Journal of Computational and Applied Mathematics,
Vol. 294,
Issue. ,
p.
251.
Manita, Anatoly
2019.
On limit laws of multi-dimensional stochastic synchronization models.
Journal of Physics: Conference Series,
Vol. 1163,
Issue. ,
p.
012060.
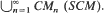 CMn (SCM). Characterization theorems for these classes are given in terms of zeros and poles of Laplace transforms. The prevalence of these classes in applied probability models of practical importance is demonstrated. In particular, sufficient conditions are given for complete monotonicity and unimodality of modified renewal densities.
CMn (SCM). Characterization theorems for these classes are given in terms of zeros and poles of Laplace transforms. The prevalence of these classes in applied probability models of practical importance is demonstrated. In particular, sufficient conditions are given for complete monotonicity and unimodality of modified renewal densities.
