In this paper, we study asymptotic behaviors of a subcritical branching Brownian motion with drift 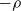$-\rho$, killed upon exiting 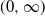$(0, \infty)$, and offspring distribution 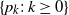$\{p_k{:}\; k\ge 0\}$. Let 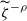$\widetilde{\zeta}^{-\rho}$ be the extinction time of this subcritical branching killed Brownian motion, $\widetilde{M}_t^{-\rho}$ the maximal position of all the particles alive at time t and 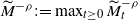$\widetilde{M}^{-\rho}:\!=\max_{t\ge 0}\widetilde{M}_t^{-\rho}$ the all-time maximal position. Let 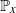$\mathbb{P}_x$ be the law of this subcritical branching killed Brownian motion when the initial particle is located at 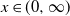$x\in (0,\infty)$. Under the assumption 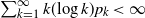$\sum_{k=1}^\infty k ({\log}\; k) p_k <\infty$, we establish the decay rates of 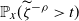$\mathbb{P}_x(\widetilde{\zeta}^{-\rho}>t)$ and 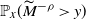$\mathbb{P}_x(\widetilde{M}^{-\rho}>y)$ as t and y respectively tend to 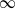$\infty$. We also establish the decay rate of 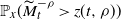$\mathbb{P}_x(\widetilde{M}_t^{-\rho}> z(t,\rho))$ as 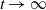$t\to\infty$, where 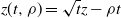$z(t,\rho)=\sqrt{t}z-\rho t$ for 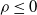$\rho\leq 0$ and $z(t,\rho)=z$ for 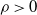$\rho>0$. As a consequence, we obtain a Yaglom-type limit theorem.