Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pontier, Monique
and
Szpirglas, Jacques
1984.
Mathematical Theory of Networks and Systems.
Vol. 58,
Issue. ,
p.
753.
Lasry, Jean-Michel
and
Lions, Pierre-Louis
1984.
Analysis and Optimization of Systems.
Vol. 63,
Issue. ,
p.
75.
Pontier, Monique
and
Szpirglas, Jacques
1984.
Filtering and Control of Random Processes.
Vol. 61,
Issue. ,
p.
243.
Pontier, M.
and
Szpirglas, J.
1984.
Linear stochastic control with constraints.
IEEE Transactions on Automatic Control,
Vol. 29,
Issue. 12,
p.
1100.
López, F.J.
San Miguel, M.
and
Sanz, G.
1995.
Lagrangean Methods and Optimal Stopping.
Optimization,
Vol. 34,
Issue. 4,
p.
317.

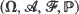 , and a non-negative real
, and a non-negative real