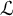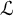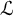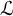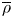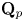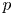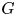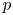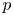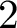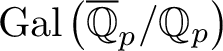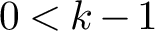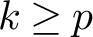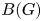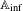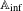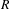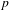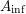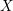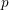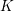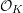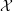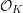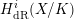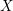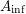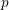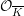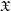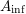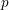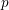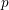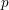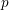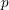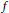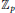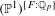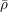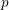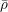Refine search
Actions for selected content:
27 results
 $ \epsilon $-ISOMORPHISMS FOR RANK ONE
$ \epsilon $-ISOMORPHISMS FOR RANK ONE  $( \varphi , \Gamma )$-MODULES OVER LUBIN-TATE ROBBA RINGS
$( \varphi , \Gamma )$-MODULES OVER LUBIN-TATE ROBBA RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1895-1994
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Overconvergence of étale
 $(\varphi,\Gamma)$-modules in families
$(\varphi,\Gamma)$-modules in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 10 July 2025, pp. 555-593
- Print publication:
- March 2025
-
- Article
- Export citation
On Greenberg–Benois
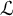 $\mathcal {L}$-invariants and Fontaine–Mazur
$\mathcal {L}$-invariants and Fontaine–Mazur 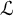 $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1141-1160
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Syntomic cycle classes and prismatic Poincaré duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 07 October 2024, pp. 2322-2365
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Completed prismatic F-crystals and crystalline Zp-local systems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1101-1166
- Print publication:
- May 2024
-
- Article
- Export citation
Faltings’ main p-adic comparison theorems for non-smooth schemes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 12 January 2024, pp. 426-458
- Print publication:
- April 2025
-
- Article
- Export citation
G-valued crystalline deformation rings in the Fontaine–Laffaille range
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1791-1832
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
p-adic Eichler–Shimura maps for the modular curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1214-1249
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A
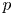 $p$-adic monodromy theorem for de Rham local systems
$p$-adic monodromy theorem for de Rham local systems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 15 December 2022, pp. 2157-2205
- Print publication:
- December 2022
-
- Article
- Export citation
REDUCTIONS OF
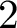 $2$-DIMENSIONAL SEMISTABLE REPRESENTATIONS WITH LARGE
$2$-DIMENSIONAL SEMISTABLE REPRESENTATIONS WITH LARGE  $\mathcal L$-INVARIANT
$\mathcal L$-INVARIANT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 01 April 2022, pp. 2619-2644
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Period sheaves via derived de Rham cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2021, pp. 2377-2406
- Print publication:
- November 2021
-
- Article
- Export citation
Rigid-analytic varieties with projective reduction violating Hodge symmetry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 625-640
- Print publication:
- March 2021
-
- Article
- Export citation
G-torseurs en théorie de Hodge p-adique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 24 November 2020, pp. 2076-2110
- Print publication:
- October 2020
-
- Article
- Export citation
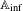 $\mathbb{A}_{\text{inf}}$ IS INFINITE DIMENSIONAL
$\mathbb{A}_{\text{inf}}$ IS INFINITE DIMENSIONAL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 11 May 2020, pp. 1983-1989
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
BREUIL–KISIN–FARGUES MODULES WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 21 January 2020, pp. 1855-1904
- Print publication:
- November 2021
-
- Article
- Export citation
The
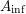 $A_{\text{inf}}$-cohomology in the semistable case
$A_{\text{inf}}$-cohomology in the semistable case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 09 September 2019, pp. 2039-2128
- Print publication:
- November 2019
-
- Article
- Export citation
Constancy of generalized Hodge–Tate weights of a local system
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 06 November 2018, pp. 2606-2642
- Print publication:
- December 2018
-
- Article
- Export citation
On the Asymptotic Growth ofBloch–Kato–Shafarevich–Tate Groups ofModular Forms Over CyclotomicExtensions
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 4 / 01 August 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 826-850
- Print publication:
- 01 August 2017
-
- Article
-
- You have access
- Export citation
VARIÉTÉS DE KISIN STRATIFIÉES ET DÉFORMATIONS POTENTIELLEMENT BARSOTTI-TATE
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 08 September 2016, pp. 1019-1064
- Print publication:
- November 2018
-
- Article
- Export citation
Density of potentially crystalline representations of fixed weight
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 1609-1647
- Print publication:
- August 2016
-
- Article
- Export citation