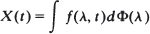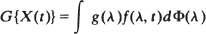Refine search
Actions for selected content:
5 results
CONSTRUCTION OF COMMUTATOR BLUEPRINTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - The Formalism of Quantum Mechanics
-
- Book:
- Quantum Mechanics
- Published online:
- 27 June 2025
- Print publication:
- 19 June 2025, pp 72-124
-
- Chapter
- Export citation
An axiomatics and a combinatorial model of creation/annihilation operators
-
- Journal:
- Mathematical Structures in Computer Science / Volume 35 / 2025
- Published online by Cambridge University Press:
- 10 April 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
20 - The Observation of Canonically Conjugates
-
- Book:
- The Einstein Paradox
- Published online:
- 14 November 2024
- Print publication:
- 28 November 2024, pp 265-265
-
- Chapter
- Export citation
Spectral generating operators for non-stationary processes
-
- Journal:
- Advances in Applied Probability / Volume 8 / Issue 4 / December 1976
- Published online by Cambridge University Press:
- 01 July 2016, pp. 831-846
- Print publication:
- December 1976
-
- Article
- Export citation