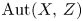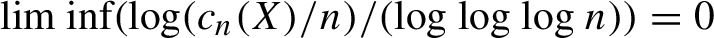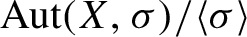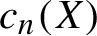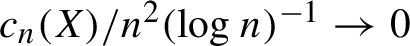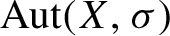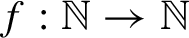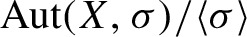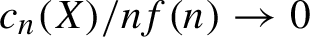Refine search
Actions for selected content:
17 results
Higher incoherence of the automorphism groups of a free group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Automorphism groups and signatures of smooth septic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-22
-
- Article
- Export citation
Distortion element in the automorphism group of a full shift
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1757-1817
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strongly Jordan property and free actions of non-abelian free groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 736-746
-
- Article
- Export citation
THE AUTOMORPHISM GROUP OF THE FRAÏSSÉ LIMIT OF FINITE HEYTING ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 07 June 2022, pp. 1310-1320
- Print publication:
- September 2023
-
- Article
- Export citation
Local finiteness and automorphism groups of low complexity subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 18 April 2022, pp. 1980-2001
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characteristic measures of symbolic dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 18 March 2021, pp. 1655-1661
- Print publication:
- May 2022
-
- Article
- Export citation
1 - Infinite Planar Graphs with Non-negative Combinatorial Curvature
-
-
- Book:
- Analysis and Geometry on Graphs and Manifolds
- Published online:
- 14 August 2020
- Print publication:
- 20 August 2020, pp 1-20
-
- Chapter
- Export citation
10 - Three-Dimensional Apeirohedra
- from III - Polytopes of Nearly Full Rank
-
- Book:
- Geometric Regular Polytopes
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 361-382
-
- Chapter
- Export citation
BOREL FUNCTORS AND INFINITARY INTERPRETATIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 05 October 2018, pp. 1434-1456
- Print publication:
- December 2018
-
- Article
- Export citation
FREE AMALGAMATION AND AUTOMORPHISM GROUPS
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 12 August 2016, pp. 936-947
- Print publication:
- September 2016
-
- Article
- Export citation
AUTOMORPHISM GROUPS OF SATURATED MODELS OF PEANO ARITHMETIC
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 25 June 2014, pp. 561-584
- Print publication:
- June 2014
-
- Article
- Export citation
ELUSIVE CODES IN HAMMING GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 286-296
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
FINITE GROUPS AS GALOIS GROUPS OF FUNCTION FIELDS WITH INFINITE FIELD OF CONSTANTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 14 May 2010, pp. 301-312
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
AUTOMORPHISM GROUPS OF THE IMPRIMITIVE COMPLEX REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 123-138
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
AUTOMORPHISM GROUPS OF FREE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 341-345
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Algebras with Transitive Automorphism Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 2 / 01 June 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 224-226
- Print publication:
- 01 June 1986
-
- Article
-
- You have access
- Export citation