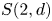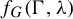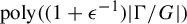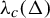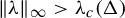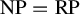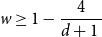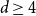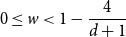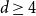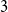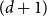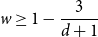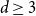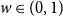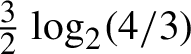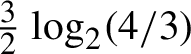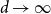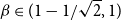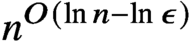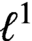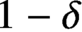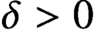Refine search
Actions for selected content:
36 results
Glauber dynamics for the hard-core model on bounded-degree
 $H$-free graphs
$H$-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The distance on the slightly supercritical random series–parallel graph
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probabilistic voting models with varying speeds of Correlation decay
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 35-64
- Print publication:
- March 2025
-
- Article
- Export citation
Hypergraph independence polynomials with a zero close to the origin
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 486-490
-
- Article
- Export citation
Bounded Littlewood identity related to alternating sign matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On level line fluctuations of SOS surfaces above a wall
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e91
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-hereditary covers of Temperley–Lieb algebras and relative dominant dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algorithms for the ferromagnetic Potts model on expanders
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 April 2024, pp. 487-517
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 2647-2711
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics of pure dimer coverings on rail yard graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 October 2023, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the zeroes of hypergraph independence polynomials
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 21 September 2023, pp. 65-84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weakly interacting oscillators on dense random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 June 2023, pp. 255-278
- Print publication:
- March 2024
-
- Article
- Export citation
Counting independent sets in amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 May 2023, pp. 958-1012
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness of the Gibbs measure for the 4-state anti-ferromagnetic Potts model on the regular tree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 07 September 2022, pp. 158-182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A complete proof that square ice entropy is
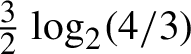 $\tfrac 32\log _{2} (4/3)$
$\tfrac 32\log _{2} (4/3)$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 1847-1908
- Print publication:
- June 2023
-
- Article
- Export citation
Independent sets of a given size and structure in the hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 702-720
-
- Article
- Export citation
More on zeros and approximation of the Ising partition function
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e46
-
- Article
-
- You have access
- Open access
- Export citation
Polynomial-time approximation algorithms for the antiferromagnetic Ising model on line graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 12 April 2021, pp. 905-921
-
- Article
- Export citation
The replica symmetric phase of random constraint satisfaction problems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 03 December 2019, pp. 346-422
-
- Article
- Export citation
Weighted counting of solutions to sparse systems of equations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 15 April 2019, pp. 696-719
-
- Article
- Export citation

































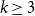
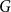
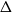
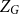
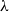
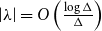
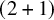
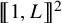 with zero boundary conditions and nonnegative heights (a floor at height
with zero boundary conditions and nonnegative heights (a floor at height 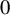
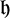
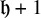
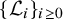
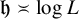
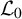
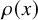
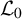
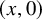
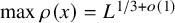
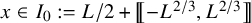 . It is believed that rescaling
. It is believed that rescaling