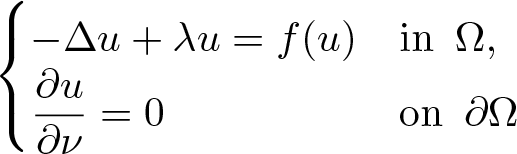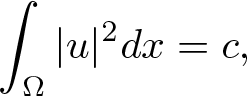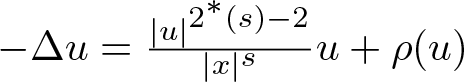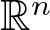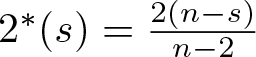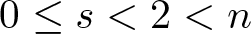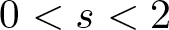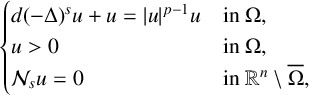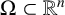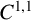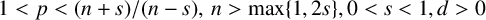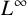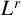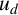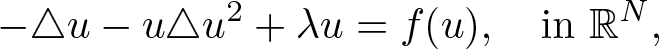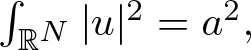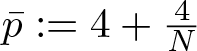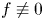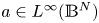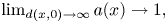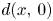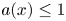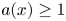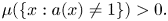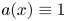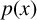Refine search
Actions for selected content:
133 results
Normalized multi-bump solutions of nonlinear Hartree equation with steep potential well
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 October 2025, pp. 1-37
-
- Article
- Export citation
A k-Hessian equation with a power nonlinearity source and self-similarity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-25
-
- Article
- Export citation
Smooth solutions to the Christoffel–Minkowski problem in hyperbolic space
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-29
-
- Article
- Export citation
Optimal boundary regularity of proper harmonic maps between asymptotically hyperbolic spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-38
-
- Article
- Export citation
Hardy-type inequalities for the drifting p-Laplace operator and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 August 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The moving plane method and the uniqueness of high-order elliptic equation with GJMS operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 July 2025, pp. 1-45
-
- Article
- Export citation
The Dirichlet problem of generalized special Lagrangian type equations and curvature version
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 April 2025, pp. 1-27
-
- Article
- Export citation
Numerical solution of a PDE arising from prediction with expert advice
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solutions with prescribed mass for L2-supercritical NLS equations under Neumann boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a perturbed critical semilinear equation with singularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 February 2025, pp. 1-35
-
- Article
- Export citation
A sharp threshold for Trudinger–Moser type inequalities with logarithmic kernels in dimension N
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-39
-
- Article
- Export citation
ASYMPTOTIC BEHAVIOUR OF THE LEAST ENERGY SOLUTIONS TO FRACTIONAL NEUMANN PROBLEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 178-209
- Print publication:
- April 2025
-
- Article
- Export citation
Normalized solutions to the quasilinear Schrödinger equations with combined nonlinearities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 349-387
-
- Article
- Export citation
VISCOSITY SOLUTIONS TO THE INFINITY LAPLACIAN EQUATION WITH SINGULAR NONLINEAR TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 345-374
- Print publication:
- December 2024
-
- Article
- Export citation
A class of Hessian quotient equations in de Sitter space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 805-821
- Print publication:
- September 2024
-
- Article
- Export citation
Multiplicity of positive solutions for a class of nonhomogeneous elliptic equations in the hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 February 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Qualitative properties of solutions for system involving the fractional Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1-16
-
- Article
- Export citation
On the existence of a nodal solution for p-Laplacian equations depending on the gradient
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 31 January 2024, pp. 1492-1513
- Print publication:
- August 2025
-
- Article
- Export citation
MULTIPLE SOLUTIONS FOR
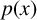 $p(x)$-LAPLACIAN EQUATIONS WITH NONLINEARITY SUBLINEAR AT ZERO
$p(x)$-LAPLACIAN EQUATIONS WITH NONLINEARITY SUBLINEAR AT ZERO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 346-354
- Print publication:
- October 2024
-
- Article
- Export citation
On generalized eigenvalue problems of fractional (p, q)-Laplace operator with two parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1385-1430
- Print publication:
- August 2025
-
- Article
- Export citation