Refine search
Actions for selected content:
48 results
Meta algebras and biorthogonal rational functions: The Hahn case
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 September 2025, e139
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sojourn functionals of time-dependent
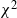 $\chi^2$-random fields on two-point homogeneous spaces
$\chi^2$-random fields on two-point homogeneous spaces
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 13 June 2025, pp. 1-20
-
- Article
- Export citation
Hausdorff moment transforms and their performance
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INVERSE CONNECTION FORMULAE FOR GENERALISED BESSEL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 480-487
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the kernel of the
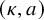 $(\kappa ,a)$-Generalized fourier transform
$(\kappa ,a)$-Generalized fourier transform
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 August 2023, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral analysis of bilateral birth–death processes: some new explicit examples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 1193-1221
- Print publication:
- December 2022
-
- Article
- Export citation
Error bounds for the asymptotic expansions of the Hermite polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 26 January 2022, pp. 417-440
- Print publication:
- April 2023
-
- Article
- Export citation
An algebraic treatment of the Askey biorthogonal polynomials on the unit circle
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 October 2021, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HEDGEHOGS IN LEHMER’S PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 07 September 2021, pp. 236-242
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
McKay matrices for finite-dimensional Hopf algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2021, pp. 686-731
- Print publication:
- June 2022
-
- Article
- Export citation
GENERALIZED FINITE POLYLOGARITHMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 February 2020, pp. 66-80
- Print publication:
- January 2021
-
- Article
- Export citation
A Spectral Identity on Jacobi Polynomials and its Analytic Implications
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 3 / 01 September 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 473-482
- Print publication:
- 01 September 2018
-
- Article
-
- You have access
- Export citation
Mixed Spectral Method for Heat Transfer Using Generalised Hermite Functions and Legendre Polynomials
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 19 October 2016, pp. 448-465
- Print publication:
- November 2016
-
- Article
- Export citation
EXT-FINITE MODULES FOR WEAKLY SYMMETRIC ALGEBRAS WITH RADICAL CUBE ZERO
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 108-121
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Generating Some Symmetric Semi-classical Orthogonal Polynomials
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 4 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 877-890
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
FILTERED POLYNOMIAL APPROXIMATION ON THE SPHERE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 27 October 2015, pp. 162-163
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Semiclassical orthogonal polynomial systems on nonuniform lattices, deformations of the Askey table, and analogues of isomonodromy
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 127-234
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Resultants of Chebyshev Polynomials: the First, Second, Third, and Fourth Kinds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 423-431
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
RANDOM WALKS, ELLIPTIC INTEGRALS AND RELATED CONSTANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 26 November 2013, pp. 166-167
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
A GENERATING FUNCTION OF THE SQUARES OF LEGENDRE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 22 March 2013, pp. 125-131
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation

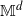
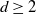
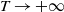
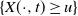
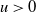

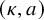
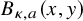
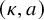
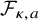
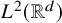
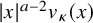
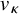
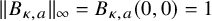
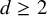
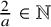
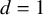
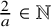
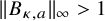
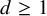
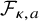
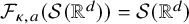
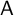
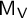
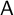
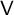
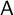
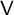
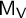
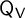
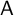
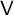
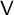
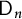
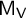
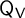
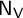
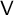
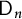
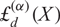
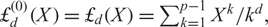
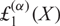
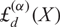
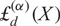
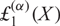
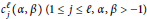
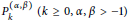


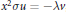
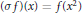

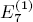 q-Painlevé system.
q-Painlevé system.