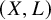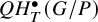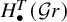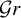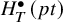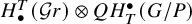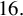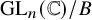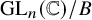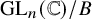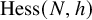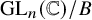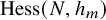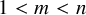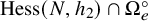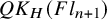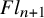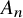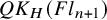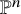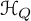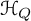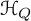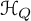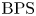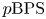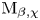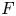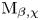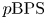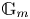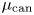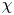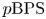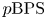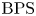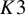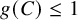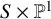Refine search
Actions for selected content:
89 results
Quantum K theory of Grassmannians, Wilson line operators and Schur bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 September 2025, e140
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-BPS categories for symmetric quivers with potential
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 16 September 2025, pp. 1799-1854
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The log-open correspondence for two-component Looijenga pairs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Open WDVV equations and Frobenius structures for toric Calabi-Yau 3-folds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 April 2025, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A mirror theorem for Gromov-Witten theory without convexity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 April 2025, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Peterson-Lam-Shimozono’s theorem is an affine analogue of quantum Chevalley formula
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
k-leaky double Hurwitz descendants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 March 2025, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative quantum cohomology of the Chiang Lagrangian
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 March 2025, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasimaps to moduli spaces of sheaves
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 March 2025, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coordinate rings of regular nilpotent Hessenberg varieties in the open opposite schubert cell
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 February 2025, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A presentation of the torus-equivariant quantum K-theory ring of flag manifolds of type A, Part II: quantum double Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On quasimap invariants of moduli spaces of Higgs bundles
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GV and GW invariants via the enhanced movable cone
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the asymptotic enumerativity property for Fano manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 November 2024, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DT INVARIANTS FROM VERTEX ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 291-339
- Print publication:
- January 2025
-
- Article
- Export citation
Flags of sheaves, quivers and symmetric polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 September 2024, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical curves in abelian surfaces I: enumeration of curves passing through points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 109-148
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BPS invariants from p-adic integrals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1525-1550
- Print publication:
- July 2024
-
- Article
- Export citation
Quasimaps to moduli spaces of sheaves on a
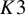 $K3$ surface
$K3$ surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 May 2024, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Logarithmic Donaldson–Thomas theory
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 April 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation