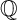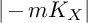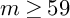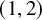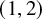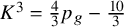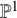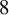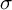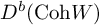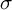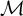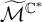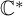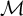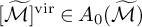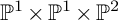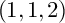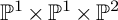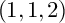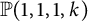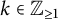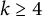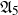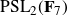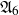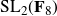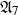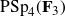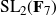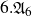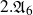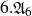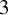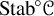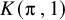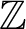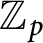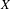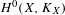Refine search
Actions for selected content:
47 results
On the irreducibility of Hessian loci of cubic hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e80
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO NON-VANISHING RESULTS CONCERNING THE ANTI-CANONICAL BUNDLE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 201-218
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIGNESS OF THE TANGENT BUNDLE OF A FANO THREEFOLD WITH PICARD NUMBER TWO
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 104-133
- Print publication:
- March 2025
-
- Article
- Export citation
BIRATIONAL GEOMETRY OF SEXTIC DOUBLE SOLIDS WITH A COMPOUND
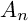 $A_n$ SINGULARITY
$A_n$ SINGULARITY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 970-1021
- Print publication:
- December 2024
-
- Article
- Export citation
Quasimaps to moduli spaces of sheaves on a
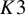 $K3$ surface
$K3$ surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 May 2024, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-stable smooth Fano threefolds of Picard rank two
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 20 March 2024, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EFFECTIVE UPPER BOUND FOR ANTI-CANONICAL VOLUMES OF SINGULAR FANO THREEFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 2631-2646
- Print publication:
- November 2024
-
- Article
- Export citation
NOTE ON THE THREE-DIMENSIONAL LOG CANONICAL ABUNDANCE IN CHARACTERISTIC
 $>3$
$>3$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 694-723
- Print publication:
- September 2024
-
- Article
- Export citation
ON THE ANTI-CANONICAL GEOMETRY OF WEAK
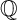 $\mathbb {Q}$-FANO THREEFOLDS, III
$\mathbb {Q}$-FANO THREEFOLDS, III
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 23-47
- Print publication:
- March 2024
-
- Article
- Export citation
Simple fibrations in
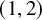 $(1,2)$-surfaces
$(1,2)$-surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 June 2023, e43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTRINSIC STABILIZER REDUCTION AND GENERALIZED DONALDSON–THOMAS INVARIANTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 1987-2025
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-STABLE DIVISORS IN
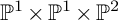 $\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$ OF DEGREE
$\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$ OF DEGREE 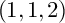 $(1,1,2)$
$(1,1,2)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 686-714
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the smooth blowups of
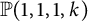 $\mathbb {P}(1,1,1,k)$ in torus-invariant subvarieties
$\mathbb {P}(1,1,1,k)$ in torus-invariant subvarieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 March 2023, pp. 1152-1163
- Print publication:
- December 2023
-
- Article
- Export citation
Finite quasisimple groups acting on rationally connected threefolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 06 December 2022, pp. 531-568
- Print publication:
- May 2023
-
- Article
- Export citation
On canonical Fano intrinsic quadrics
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 07 November 2022, pp. 288-309
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability conditions for contraction algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EFFECTIVE BOUNDS FOR THE NUMBER OF MMP-SERIES OF A SMOOTH THREEFOLD
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 18 December 2020, pp. 106-113
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Homology supported in Lagrangian submanifolds in mirror quintic threefolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 709-724
- Print publication:
- September 2021
-
- Article
- Export citation
Threefolds fibred by mirror sextic double planes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 24 June 2020, pp. 1305-1346
- Print publication:
- October 2021
-
- Article
- Export citation
THE INTEGRAL HODGE CONJECTURE FOR 3-FOLDS OF KODAIRA DIMENSION ZERO
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 18 February 2020, pp. 1697-1717
- Print publication:
- September 2021
-
- Article
- Export citation








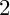
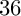
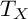


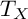
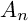
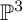
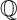
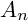
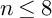
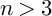
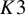

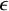


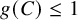
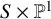
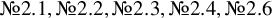 and
and 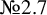 are K-stable, and we also prove that smooth Fano threefolds in the family
are K-stable, and we also prove that smooth Fano threefolds in the family 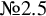 that satisfy one very explicit generality condition are K-stable.
that satisfy one very explicit generality condition are K-stable.