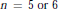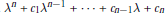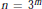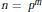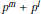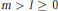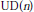Refine search
Actions for selected content:
18 results
Irreducible factors of a polynomial
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 573-582
-
- Article
- Export citation
AN ALGEBRAIC INTERPRETATION OF THE SUPER CATALAN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 498-506
- Print publication:
- June 2024
-
- Article
- Export citation
AN EFFECTIVE ANALYTIC FORMULA FOR THE NUMBER OF DISTINCT IRREDUCIBLE FACTORS OF A POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 339-356
- Print publication:
- December 2022
-
- Article
- Export citation
A NOTE ON GIRSTMAIR’S IRREDUCIBILITY CRITERION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 04 November 2021, pp. 62-66
- Print publication:
- August 2022
-
- Article
- Export citation
A CLASS OF FIELDS WITH A RESTRICTED MODEL COMPLETENESS PROPERTY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 26 March 2021, pp. 701-708
- Print publication:
- June 2021
-
- Article
- Export citation
On the degree of repeated radical extensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 23 November 2020, pp. 877-885
- Print publication:
- December 2021
-
- Article
- Export citation
CYCLOTOMIC FACTORS OF BORWEIN POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 28 March 2019, pp. 41-47
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
SMOOTH VALUES OF POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 245-261
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Characterizing Distinguished Pairs by Using Liftings of Irreducible Polynomials
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-232
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
Ruin Probability in a Generalised Risk Process under Rates of Interest with Homogenous Markov Chains
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 4 / Issue 3 / August 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 283-300
- Print publication:
- August 2014
-
- Article
- Export citation
Solvability by Real Radicals and Fermat Primes
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 2 / 01 June 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 229-236
- Print publication:
- 01 June 2004
-
- Article
-
- You have access
- Export citation
Problèmes de ruine en théorie du risque à temps discret avec horizon fini
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 527-542
- Print publication:
- September 2003
-
- Article
- Export citation
Probabilité de ruine éventuelle dans un modèle de risque à temps discret
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 543-556
- Print publication:
- September 2003
-
- Article
- Export citation
Essential Dimensions of Algebraic Groups and a Resolution Theorem for G-Varieties
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 5 / 01 October 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1018-1056
- Print publication:
- 01 October 2000
-
- Article
-
- You have access
- Export citation
On a Theorem of Hermite and Joubert
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 1 / 01 February 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 69-95
- Print publication:
- 01 February 1999
-
- Article
-
- You have access
- Export citation
Comparaison de Deux Mesures de Polynômes
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 4 / 01 December 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 438-444
- Print publication:
- 01 December 1995
-
- Article
-
- You have access
- Export citation
On Schur's conjecture
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 312-357
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
A Multivariable form of the Fundamental Theorem of Algebra
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 3 / 01 September 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 271-272
- Print publication:
- 01 September 1983
-
- Article
-
- You have access
- Export citation
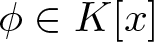
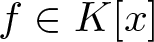
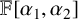
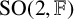
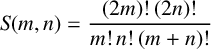
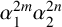


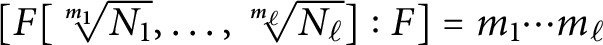
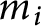
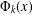
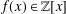
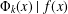
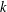
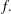
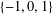
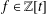
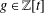
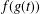
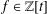
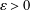
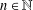
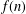
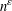


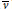
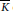
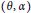
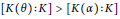

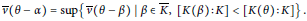
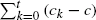 is bounded as the time
is bounded as the time