Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-31T06:55:42.074Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizing Distinguished Pairs by Using Liftings of Irreducible Polynomials

Published online by Cambridge University Press:  20 November 2018

Kamal Aghigh  and
Azadeh Nikseresht
Kamal Aghigh
Affiliation:
Department of Mathematics, K. N. Toosi University of Technology, P.O.Box 16315-1618, Tehran, Iran. e-mail: aghigh@kntu.ac.ir e-mail: a.nikseresht@mail.kntu.ac.ir
Azadeh Nikseresht
Affiliation:
Department of Mathematics, K. N. Toosi University of Technology, P.O.Box 16315-1618, Tehran, Iran. e-mail: aghigh@kntu.ac.ir e-mail: a.nikseresht@mail.kntu.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $v$ be a henselian valuation of any rank of a field $K$ and let 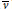$\bar{v}$ be the unique extension of $v$ to a fixed algebraic closure 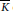$\overline{K}$ of $K$ . In 2005, we studied properties of those pairs 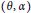$\left( \theta ,\,\alpha\right)$ of elements of 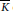$\overline{K}$ with 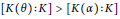$\left[ K\left( \theta\right):K \right]\,>\,\left[ K\left( \alpha\right):K \right]$ where $\alpha $ is an element of smallest degree over $K$ such that

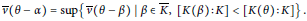$$\bar{v}\left( \theta \,-\,\alpha\right)\,=\,\sup \left\{ \bar{v}\left( \theta \,-\,\beta\right)\,|\,\beta \,\in \,\bar{K},\,\left[ K\left( \beta\right):K \right]\,<\,\left[ K\left( \theta\right):K \right] \right\}\,.$$

Such pairs are referred to as distinguished pairs. We use the concept of liftings of irreducible polynomials to give a different characterization of distinguished pairs.

Keywords

12J1012J2512E05valued fieldsnon-Archimedean valued fieldsirreducible polynomials

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 225 - 232
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Aghigh, K. and Khanduja, S. K., On the main invariant of elements algebraic over a Henselian valued field. Proc. Edinb. Math. Soc. 45 (2002), no. 1, 219–227.Google Scholar
[2] Aghigh, K. and Khanduja, S. K., On chains associated with elements algebraic over a Henselian valued field. Algebra Colloq. 12 (2005), no. 4, 607–616. http://dx.doi.Org/10.1142/S100538670500057X Google Scholar
[3] Alexandru, V., Popescu, N., and Zaharescu, A., A theorem of characterization of residual transcendental extensions of a valuation. J. Math. Kyoto Univ. 28 (1988), no. 4, 579–592.Google Scholar
[4] Alexandru, V., Popescu, N., and Zaharescu, A., Minimal pairs of definition of a residual transcendental extension of a valuation. J. Math. Kyoto Univ. 30 (1990), no. 2, 207–225.Google Scholar
[5] Bhatia, S. and Khanduja, S. K., On extensions generated by roots of lifting polynomials. Mathematika 49 (2002), no. 1–2,107–118. http://dx.doi.Org/10.1112/S0025579300016107 Google Scholar
[6] Bishoni, A. and Khanduja, S. K., On Eisenstein-Dumas and generalized Schonemann polynomials. Comm. Algebra 38 (2010), no. 9, 3163–3173. http://dx.doi.Org/10.1080/00927870903164669 Google Scholar
[7] Bishoni, A., Kumar, S., and Khanduja, S. K., On liftings of powers of irreducible polynomials. J. Algebra Appl. 12 (2013), no. 5,1250222. http://dx.doi.Org/10.1142/S0219498812502222 Google Scholar
[8] Brown, R. and Merzel, J. L., Invariants of defectless irreducible polynomials. J. Algebra Appl. 9 (2010), no. 4, 603–631. http://dx.doi.Org/1 0.1142/S021 949881 0004130 Google Scholar
[9] Khanduja, S. K., On valuations ofK(x). Proc. Edinburgh Math. Soc. 35 (1992), no. 3, 419–426. http://dx.doi.org/10.1017/S0013091500005708 Google Scholar
[10] Khanduja, S. K. and Kumar, S., On prolongation of valuations via Newton polygons and liftings of polynomials. J. Pure Appl. Algebra 216 (2012), no. 12, 2648–2656. http://dx.doi.Org/10.1016/j.jpaa.2012.03.034 Google Scholar
[11] Khanduja, S. K. and Saha, J., On a generalization of Eisenstein's irreducibility criterion. Mathematika 44 (1997), no. 1, 37–41. http://dx.doi.Org/10.1112/S0025579300011931 Google Scholar
[12] Khanduja, S. K. and Saha, J., A generalized fundamental principle. Mathematika 46 (1999), no. 1, 83–92. http://dx.doi.Org/10.1112/S0025579300007580 Google Scholar
[13] Popescu, N. and Zaharescu, A., On the structure of the irreducible polynomials over local fields. J. Number Theory 52 (1995), no. 1, 98–118. http://dx.doi.Org/10.1006/jnth.1995.1058 Google Scholar