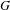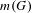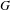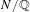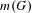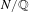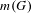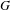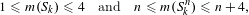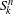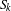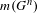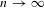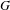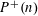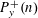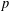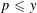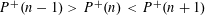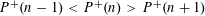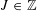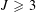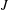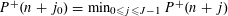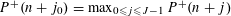The minimal ramification problem may be considered as a quantitative version of the inverse Galois problem. For a nontrivial finite group 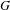 $G$, let
$G$, let 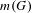 $m(G)$ be the minimal integer
$m(G)$ be the minimal integer  $m$ for which there exists a
$m$ for which there exists a 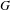 $G$-Galois extension
$G$-Galois extension 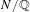 $N/\mathbb{Q}$ that is ramified at exactly
$N/\mathbb{Q}$ that is ramified at exactly  $m$ primes (including the infinite one). So, the problem is to compute or to bound
$m$ primes (including the infinite one). So, the problem is to compute or to bound 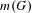 $m(G)$.
$m(G)$.
In this paper, we bound the ramification of extensions 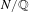 $N/\mathbb{Q}$ obtained as a specialization of a branched covering
$N/\mathbb{Q}$ obtained as a specialization of a branched covering  $\unicode[STIX]{x1D719}:C\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$. This leads to novel upper bounds on
$\unicode[STIX]{x1D719}:C\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$. This leads to novel upper bounds on 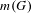 $m(G)$, for finite groups
$m(G)$, for finite groups 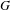 $G$ that are realizable as the Galois group of a branched covering. Some instances of our general results are:
$G$ that are realizable as the Galois group of a branched covering. Some instances of our general results are: 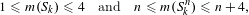 $$\begin{eqnarray}1\leqslant m(S_{k})\leqslant 4\quad \text{and}\quad n\leqslant m(S_{k}^{n})\leqslant n+4,\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant m(S_{k})\leqslant 4\quad \text{and}\quad n\leqslant m(S_{k}^{n})\leqslant n+4,\end{eqnarray}$$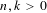 $n,k>0$. Here
$n,k>0$. Here 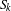 $S_{k}$ denotes the symmetric group on
$S_{k}$ denotes the symmetric group on 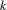 $k$ letters, and
$k$ letters, and 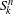 $S_{k}^{n}$ is the direct product of
$S_{k}^{n}$ is the direct product of  $n$ copies of
$n$ copies of 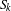 $S_{k}$. We also get the correct asymptotic of
$S_{k}$. We also get the correct asymptotic of 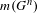 $m(G^{n})$, as
$m(G^{n})$, as 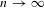 $n\rightarrow \infty$ for a certain class of groups
$n\rightarrow \infty$ for a certain class of groups 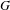 $G$.
$G$.
Our methods are based on sieve theory results, in particular on the Green–Tao–Ziegler theorem on prime values of linear forms in two variables, on the theory of specialization in arithmetic geometry, and on finite group theory.