Hostname: page-component-7dd5485656-6kn8j Total loading time: 0 Render date: 2025-10-30T16:03:31.630Z Has data issue: false hasContentIssue false
  • English
  • Français

SUR LES PLUS GRANDS FACTEURS PREMIERSD’ENTIERS CONSÉCUTIFS

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  05 April 2018

Zhiwei Wang (Nancy)
Zhiwei Wang (Nancy)*
Affiliation:
Institut Élie Cartan de Lorraine, Université de Lorraine, UMR 7502, 54506 Vandœuvre-lès-Nancy, France email zhiwei.wang@univ-lorraine.fr
Get access

Abstract

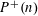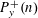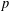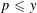Let $P^{+}(n)$ denote the largest prime factor of the integer $n$ and $P_{y}^{+}(n)$ denote the largest prime factor $p$ of $n$ which satisfies $p\leqslant y$ . In this paper, first we show that the triple consecutive integers with the two patterns 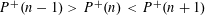$P^{+}(n-1)>P^{+}(n)<P^{+}(n+1)$ and 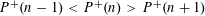$P^{+}(n-1)<P^{+}(n)>P^{+}(n+1)$ have a positive proportion respectively. More generally, with the same methods we can prove that for any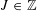$J\in \mathbb{Z}$ , 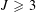$J\geqslant 3$ , the 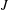$J$ -tuple consecutive integers with the two patterns 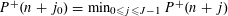$P^{+}(n+j_{0})=\min _{0\leqslant j\leqslant J-1}P^{+}(n+j)$ and 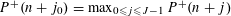$P^{+}(n+j_{0})=\max _{0\leqslant j\leqslant J-1}P^{+}(n+j)$ also have a positive proportion, respectively. Second, for 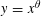$y=x^{\unicode[STIX]{x1D703}}$ with 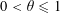$0<\unicode[STIX]{x1D703}\leqslant 1$ we show that there exists a positive proportion of integers $n$ such that 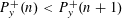$P_{y}^{+}(n)<P_{y}^{+}(n+1)$ . Specifically, we can prove that the proportion of integers $n$ such that 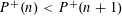$P^{+}(n)<P^{+}(n+1)$ is larger than 0.1356, which improves the previous result “0.1063” of the author.

MSC classification

Primary: 11K65: Arithmetic functions

Information

Type
Research Article
Information
Mathematika , Volume 64 , Issue 2 , 2018 , pp. 343 - 379
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Balog, A., On triplets with descending largest prime factors. Studia Sci. Math. Hungar. 38 2001, 45–50.Google Scholar
Bombieri, E., On the large sieve. Mathematika 12 1965, 201–225.Google Scholar
Bombieri, E., Friedlander, J. B. and Iwaniec, H., Primes in arithmetic progressions to large moduli. Acta Math. 156 1986, 203–251.Google Scholar
de la Bretèche, R., Pomerance, C. and Tenenbaum, G., Products of ratios of consecutive integers. Ramanujan J. 9 2005, 131–138.CrossRefGoogle Scholar
De La Bretèche, R. and Tenenbaum, G., Propriétés statistiques des entiers friables. Ramanujan J. 9(1) 2005, 139–202.Google Scholar
De Koninck, J. M. and Doyon, N., On the distance between smooth numbers. Integers 11 2011, 647–669.CrossRefGoogle Scholar
Drappeau, S., Théorèmes de type Fouvry–Iwaniec pour les entiers friables. Compos. Math. 151(5) 2015, 828–862.Google Scholar
Erdős, P., Some unconventional problems in number theory. Astérisque 61 1979, 73–82.Google Scholar
Erdős, P. and Pomerance, C., On the largest prime factors of n and n + 1. Aequationes Math. 17(2–3) 1978, 311–321.Google Scholar
Fouvry, E., Autour du théorème de Bombieri–Vinogradov. Acta Math. 152(1) 1984, 219–244.Google Scholar
Fouvry, E. and Iwaniec, H., Primes in arithmetic progressions. Acta Arith. 42(2) 1983, 197–218.Google Scholar
Fouvry, E. and Tenenbaum, G., Entiers sans grand facteur premier en progressions arithmétiques. Proc. Lond. Math. Soc. (3) 63(3) 1991, 449–494.Google Scholar
Fouvry, E. and Tenenbaum, G., Répartition statistique des entiers sans grand facteur premier dans les progressions arithmétiques. Proc. Lond. Math. Soc. (3) 72(3) 1996, 481–514.Google Scholar
Harper, A. J., Bombieri–Vinogradov and Barban–Davenport–Halberstam type theorems for smooth numbers. Preprint, 2012, arXiv:1208.5992.Google Scholar
Hildebrand, A., On the number of positive integers ⩽x and free of prime factors >y . J. Number Theory 22 1986, 289–307.Google Scholar
Iwaniec, H., A new form of the error term in the linear sieve. Acta Arith. 37 1980, 307–320.Google Scholar
Motohashi, Y., An induction principle for the generalization of bombieri’s prime number theorem. Proc. Japan Acad. 52(6) 1976, 273–275.Google Scholar
Pan, C. D., Ding, X. Q. and Wang, Y., On the representation of every large even integer as a sum of a prime and an almost prime. Sci. Sin. 18(5) 1975, 599–610.Google Scholar
Rivat, J., On pseudo-random properties of P (n) and P (n + 1). Period. Math. Hungar. 43 2001, 121–136.Google Scholar
Tenenbaum, G., Introduction à la théorie analytique et probabiliste des nombres, 3rd edn. (Collection Échelles), Édition Belin (2008).Google Scholar
Tenenbaum, G., Some of Erdős’ unconventional problems in number theory, thirty-four years later. In Erdős Centennial (Bolyai Society Mathematical Studies 25 ), János Bolyai Mathematical Society (Budapest, 2013), 651–681.Google Scholar
Tenenbaum, G. and Wu, J., Théorie analytique et probabiliste des nombres, 307 exercices corrigés (Cours Spécialiés 2 ), Société Mathématique de France (Paris, 1996).Google Scholar
Teräväinen, J., A note on binary correlations of multiplicative functions. Preprint, 2017, arXiv:1710.01195.Google Scholar
Vinogradov, A. I., The density hypothesis for dirichet l-series. Izv. Akad. Nauk SSSR Ser. Mat. 29 1965, 903–934.Google Scholar
Wang, Z. W., On the largest prime factors of consecutive integers in short intervals. Proc. Amer. Math. Soc. 145(8) 2017, 3211–3220.CrossRefGoogle Scholar
Wolke, D., Über die mittlere verteilung der werte zahlentheoretischer funktionen auf restklassen. II. Math. Ann. 204(2) 1973, 145–153.CrossRefGoogle Scholar
Xuan, T. Z., Integers free of small prime factors in arithmetic progressions. Nagoya Math. J. 157 2000, 103–127.Google Scholar