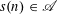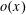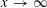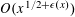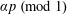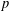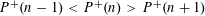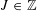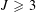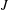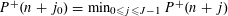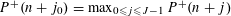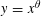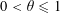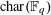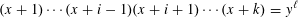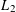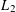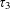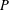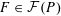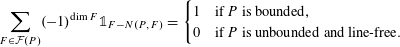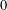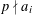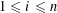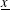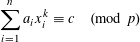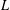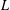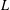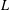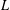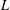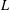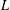Contents
Research Article
A LOCAL UNIQUENESS THEOREM FOR MINIMIZERS OF PETTY’S CONJECTURED PROJECTION INEQUALITY
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2018, pp. 1-19
-
- Article
- Export citation
ALGEBRAIC TORI AS DEGENERATIONS OF ABELIAN VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2018, pp. 303-329
-
- Article
-
- You have access
- HTML
- Export citation
A UNIFIED APPROACH TO CONTINUOUS, MEASURABLE SELECTIONS, AND SELECTIONS FOR HYPERSPACES
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 607-627
-
- Article
- Export citation
DIVISOR-SUM FIBERS
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 330-342
-
- Article
- Export citation
THE GOLDBACH PROBLEM FOR PRIMES THAT ARE SUMS OF TWO SQUARES PLUS ONE
- Part of:
-
- Published online by Cambridge University Press:
- 25 January 2018, pp. 20-70
-
- Article
- Export citation
A METRIC THEORY OF MINIMAL GAPS
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 628-636
-
- Article
- Export citation
DIFFERENTIAL GERSTENHABER–BATALIN–VILKOVISKY ALGEBRAS FOR CALABI–YAU HYPERSURFACE COMPLEMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2018, pp. 637-651
-
- Article
- Export citation
SET MAPPINGS WITH FREE SETS WHICH ARE ARITHMETIC PROGRESSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. 71-76
-
- Article
- Export citation
SUR LES PLUS GRANDS FACTEURS PREMIERSD’ENTIERS CONSÉCUTIFS
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2018, pp. 343-379
-
- Article
- Export citation
ON THE
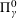 $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS AND
$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS AND 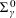 $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. 77-114
-
- Article
- Export citation
INTEGRAL MONODROMY GROUPS OF KLOOSTERMAN SHEAVES
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2018, pp. 652-678
-
- Article
- Export citation
VARIANTS OF ERDŐS–SELFRIDGE SUPERELLIPTIC CURVES AND THEIR RATIONAL POINTS
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 380-386
-
- Article
- Export citation
MONOCHROMATIC FACTORIZATIONS OF WORDS AND PERIODICITY
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. 115-123
-
- Article
- Export citation
ADDITIVE ENERGY AND THE METRIC POISSONIAN PROPERTY
- Part of:
-
- Published online by Cambridge University Press:
- 19 June 2018, pp. 679-700
-
- Article
- Export citation
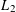 $L_{2}$ -SMALL DEVIATIONS FOR WEIGHTED STATIONARY PROCESSES
$L_{2}$ -SMALL DEVIATIONS FOR WEIGHTED STATIONARY PROCESSES
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 387-405
-
- Article
- Export citation
REDUCTION OF DIMENSION AS A CONSEQUENCE OF NORM-RESOLVENT CONVERGENCE AND APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 406-429
-
- Article
- Export citation
TERNARY DIVISOR FUNCTIONS IN ARITHMETIC PROGRESSIONS TO SMOOTH MODULI
- Part of:
-
- Published online by Cambridge University Press:
- 19 June 2018, pp. 701-729
-
- Article
- Export citation
AN INCLUSION–EXCLUSION IDENTITY FOR NORMAL CONES OF POLYHEDRAL SETS
- Part of:
-
- Published online by Cambridge University Press:
- 05 February 2018, pp. 124-136
-
- Article
- Export citation
SOLUTIONS TO DIAGONAL CONGRUENCES WITH VARIABLES RESTRICTED TO A BOX
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 430-444
-
- Article
- Export citation
TRUNCATED PRODUCT REPRESENTATIONS FOR
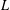 $L$ -FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
$L$ -FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. 137-158
-
- Article
- Export citation