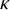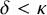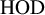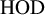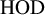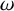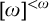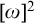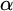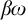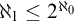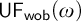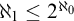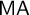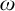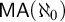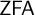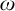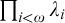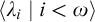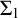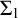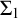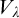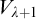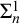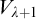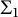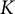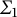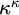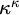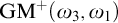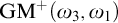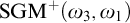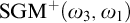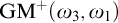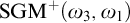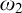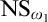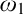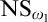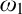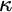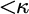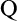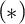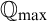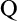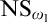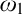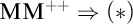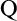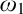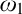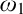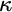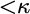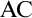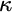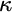Refine search
Actions for selected content:
174 results
A NOTE ON SURJECTIVE CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-15
-
- Article
- Export citation
ON THE CATEGORICITY OF COMPLETE SECOND-ORDER THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1-23
-
- Article
- Export citation
THE WEAK EXTENSION PRINCIPLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-11
-
- Article
- Export citation
ABSTRACTION PRINCIPLES AND THE SIZE OF REALITY
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 19 August 2025, pp. 1-14
-
- Article
- Export citation
UNIFORMITY NUMBERS OF THE NULL-ADDITIVE AND MEAGER-ADDITIVE IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-37
-
- Article
- Export citation
SEPARATING SUBVERSION FORCING AXIOMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 30 July 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compactness phenomena in HOD
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 July 2025, e118
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PFA AND THE DEFINABILITY OF THE NONSTATIONARY IDEAL
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-8
-
- Article
- Export citation
HIGH DIMENSIONAL COUNTABLE COMPACTNESS AND ULTRAFILTERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-21
-
- Article
- Export citation
COLORING EQUILATERAL TRIANGLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-14
-
- Article
- Export citation
MENGER AND CONSONANT SETS IN THE SACKS MODEL
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 March 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ITERATION THEOREMS FOR SUBVERSIONS OF FORCING CLASSES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1-51
- Print publication:
- March 2025
-
- Article
- Export citation
THE COVERING NUMBERS OF SOME MYCIELSKI IDEALS MAY BE DIFFERENT
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 252-277
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ON YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-16
-
- Article
- Export citation
ON FREE ULTRAFILTERS ON
 $\omega $ WITH WELL-ORDERABLE BASES IN
$\omega $ WITH WELL-ORDERABLE BASES IN  $\mathsf {ZF}$
$\mathsf {ZF}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DESCRIPTIVE PROPERTIES OF I2-EMBEDDINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On
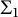 $\Sigma _1$-definable closed unbounded sets
$\Sigma _1$-definable closed unbounded sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 January 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALIZED TOWER SPECTRA
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 10 January 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON INDESTRUCTIBLE STRONGLY GUESSING MODELS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 January 2025, pp. 1-27
-
- Article
- Export citation
Forcing “
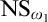 $\mathrm {NS}_{\omega _1}$ is
$\mathrm {NS}_{\omega _1}$ is 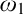 $\omega _1$-Dense” from Large Cardinals
$\omega _1$-Dense” from Large Cardinals
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 18 March 2025, p. 544
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation