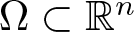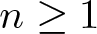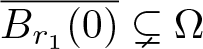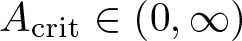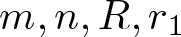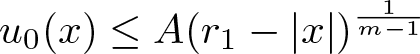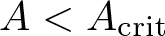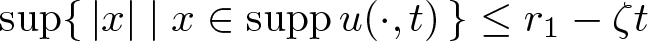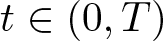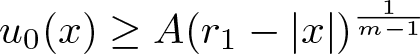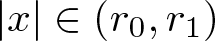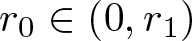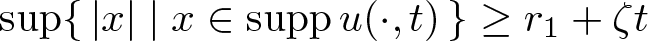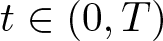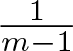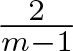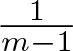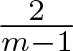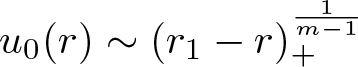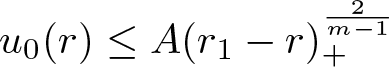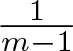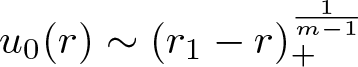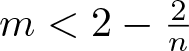1. Introduction
The present paper studies the evolution of the positivity set of solutions to a model problem with degenerate diffusion and attractive taxis, namely
 \begin{align}
\begin{cases}
\partial_t u = \nabla \cdot (u^{m-1} \nabla u - u \nabla v) & \text{in}\ \Omega \times (0, T), \\
0 = \Delta v - \mu + u, \quad \mu = \frac{1}{|\Omega|} \int_\Omega u_0, & \text{in}\ \Omega \times (0, T), \\
\partial_\nu u = \partial_\nu v = 0 & \text{on}\ \partial \Omega \times (0, T), \\
u(\cdot, 0) = u_0 & \text{in}\ \Omega,
\end{cases}
\end{align}
\begin{align}
\begin{cases}
\partial_t u = \nabla \cdot (u^{m-1} \nabla u - u \nabla v) & \text{in}\ \Omega \times (0, T), \\
0 = \Delta v - \mu + u, \quad \mu = \frac{1}{|\Omega|} \int_\Omega u_0, & \text{in}\ \Omega \times (0, T), \\
\partial_\nu u = \partial_\nu v = 0 & \text{on}\ \partial \Omega \times (0, T), \\
u(\cdot, 0) = u_0 & \text{in}\ \Omega,
\end{cases}
\end{align} where m > 1 is a given parameter and ![]() $\Omega \subset \mathbb{R}^n$ is a ball. The system (1.1) is a parabolic–elliptic simplification of the celebrated Keller–Segel model ([Reference Keller and Segel22]), which models the spatio-temporal evolution of an organism (with density u) that is partially attracted by a chemical (with concentration v) produced by itself. This chemotactic effect is modelled by the term
$\Omega \subset \mathbb{R}^n$ is a ball. The system (1.1) is a parabolic–elliptic simplification of the celebrated Keller–Segel model ([Reference Keller and Segel22]), which models the spatio-temporal evolution of an organism (with density u) that is partially attracted by a chemical (with concentration v) produced by itself. This chemotactic effect is modelled by the term ![]() $- \nabla \cdot (u \nabla v)$ and the non-directed mobility is supposed to be density-dependent and to take the form
$- \nabla \cdot (u \nabla v)$ and the non-directed mobility is supposed to be density-dependent and to take the form ![]() $\nabla \cdot (u^{m-1} \nabla u)$; see, e.g., [Reference Gurtin and MacCamy15, Reference Hillen and Painter17, Reference Painter and Hillen28] for modelling considerations.
$\nabla \cdot (u^{m-1} \nabla u)$; see, e.g., [Reference Gurtin and MacCamy15, Reference Hillen and Painter17, Reference Painter and Hillen28] for modelling considerations.
With respect to blow-up in (1.1), the exponent 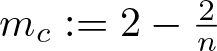 $m_c := 2 - \frac2n$ is critical: If
$m_c := 2 - \frac2n$ is critical: If ![]() $m \gt m_c$, then for all sufficiently regular, nonnegative initial data, there exist global, bounded solutions ([Reference Sugiyama31], see also [Reference Ishida, Seki and Yokota19, Reference Kowalczyk and Szymańska24]), while if
$m \gt m_c$, then for all sufficiently regular, nonnegative initial data, there exist global, bounded solutions ([Reference Sugiyama31], see also [Reference Ishida, Seki and Yokota19, Reference Kowalczyk and Szymańska24]), while if ![]() $m \in (1, m_c)$, then for all M > 0 one can find nonnegative u 0 with
$m \in (1, m_c)$, then for all M > 0 one can find nonnegative u 0 with 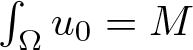 $\int_\Omega u_0 = M$ and a solution of (1.1) blowing up in finite time ([Reference Cieślak and Winkler12, Reference Sugiyama31], see also [Reference Hashira, Ishida and Yokota16, Reference Ishida and Yokota20]). Moreover, in the fully parabolic full-space setting with
$\int_\Omega u_0 = M$ and a solution of (1.1) blowing up in finite time ([Reference Cieślak and Winkler12, Reference Sugiyama31], see also [Reference Hashira, Ishida and Yokota16, Reference Ishida and Yokota20]). Moreover, in the fully parabolic full-space setting with ![]() $m = m_c \gt 1$, there is a critical mass distinguishing between global boundedness and the possibility of finite-time blow-up ([Reference Blanchet and Laurençot6, Reference Laurençot and Mizoguchi27]). Regarding the fully parabolic nondegenerate setting with potential nonlinear taxis sensitivity, we refer to [Reference Horstmann and Winkler18, Reference Ishida, Seki and Yokota19, Reference Tao and Winkler33] for global boundedness, to [Reference Winkler35] for blow-up in either finite or infinite time, and to [Reference Cao and Fuest8] (as well as to the precedents [Reference Cieślak and Stinner9–Reference Cieślak and Stinner11]) for finite-time blow-up. For an overview of further dichotomies between boundedness and blow-up for chemotaxis systems, see the surveys [Reference Bellomo, Bellouquid, Tao and Winkler2, Reference Lankeit and Winkler25].
$m = m_c \gt 1$, there is a critical mass distinguishing between global boundedness and the possibility of finite-time blow-up ([Reference Blanchet and Laurençot6, Reference Laurençot and Mizoguchi27]). Regarding the fully parabolic nondegenerate setting with potential nonlinear taxis sensitivity, we refer to [Reference Horstmann and Winkler18, Reference Ishida, Seki and Yokota19, Reference Tao and Winkler33] for global boundedness, to [Reference Winkler35] for blow-up in either finite or infinite time, and to [Reference Cao and Fuest8] (as well as to the precedents [Reference Cieślak and Stinner9–Reference Cieślak and Stinner11]) for finite-time blow-up. For an overview of further dichotomies between boundedness and blow-up for chemotaxis systems, see the surveys [Reference Bellomo, Bellouquid, Tao and Winkler2, Reference Lankeit and Winkler25].
Much less studied are support propagation properties of (1.1) – in contrast to those of its taxis-free relative
the porous medium equation (PME) (where again m > 1 is a given parameter), for which finite speed of propagation and the existence of waiting times constitute celebrated phenomena. The former states that the positivity set of solutions to nonnegative, nontrivial initial u 0 with compact support does not grow infinitely fast ([Reference Vazquez34, Theorem 14.6]). This contrasts the nondegenerate heat equation, (1.2) with m = 1, whose solutions to such initial data become immediately positive by the strict maximum principle.
While solutions to the PME eventually propagate to all compact subsets of the domain in finite time ([Reference Vazquez34, Theorem 14.3]), the question whether the support already needs to grow near t = 0 is more delicate. As it turns out, the answer is completely determined by the flatness of u 0 near a point ![]() $x_0 \in \operatorname{supp} u_0$: If
$x_0 \in \operatorname{supp} u_0$: If 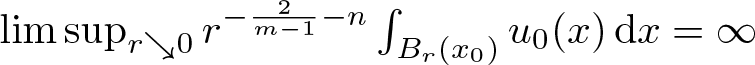 $\limsup_{r \searrow 0} r^{-\frac{2}{m-1}-n} \int_{B_r(x_0)} u_0(x) \,\mathrm{d}x = \infty$, the support near x 0 immediately expands, while, if this quantity is finite, then there is a so-called waiting time upon which the support near x 0 stays constant before it starts to grow, see [Reference Alikakos1, propsition 4.2]. In particular, if the initial data are of the form
$\limsup_{r \searrow 0} r^{-\frac{2}{m-1}-n} \int_{B_r(x_0)} u_0(x) \,\mathrm{d}x = \infty$, the support near x 0 immediately expands, while, if this quantity is finite, then there is a so-called waiting time upon which the support near x 0 stays constant before it starts to grow, see [Reference Alikakos1, propsition 4.2]. In particular, if the initial data are of the form ![]() $u_0(x) = C (|x|-r_1)_+^\alpha$ for
$u_0(x) = C (|x|-r_1)_+^\alpha$ for ![]() $|x|$ close to r 1, a waiting time phenomenon near x 0 occurs if and only if
$|x|$ close to r 1, a waiting time phenomenon near x 0 occurs if and only if 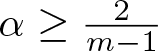 $\alpha \ge \frac{2}{m-1}$. Similar results have been obtained for other degenerate equations as well, see for instance [Reference Dal Passo, Giacomelli and Grün13] both for doubly nonlinear and for higher order equations and [Reference Laurençot and Matioc26] for a repulsive–repulsive fully cross-diffusive system.
$\alpha \ge \frac{2}{m-1}$. Similar results have been obtained for other degenerate equations as well, see for instance [Reference Dal Passo, Giacomelli and Grün13] both for doubly nonlinear and for higher order equations and [Reference Laurençot and Matioc26] for a repulsive–repulsive fully cross-diffusive system.
On the other hand, degenerate diffusion as in (1.2) alone cannot cause a retraction of the free boundary; the size of the support can never strictly decrease ([Reference Vazquez34, proposition 14.1]). This raises the question whether an additional mechanism added to the PME can lead to initial support shrinking. A natural such candidate is attractive taxis: As discussed above, the thereby introduced tendency towards aggregation is in some situations sufficiently strong to completely overcome the stabilizing effect of diffusion in the sense that it causes (finite-time) blow-up, so it is conceivable that it may also reverse the direction of movement of the free boundary, at least for some time.
This is indeed the case: Initial support shrinking has been detected in [Reference Fischer14] for a chemotaxis system with prevention of overcrowding introduced in [Reference Burger, Di Francesco and Dolak-Struss7], and in [Reference Xu, Ji, Mei and Yin36] for a fully parabolic chemotaxis–consumption model (where one then also needs to impose certain conditions on ![]() $v(\cdot, 0)$). On the other hand, [Reference Black4] shows that solutions to degenerate chemotaxis systems may not form dead-cores in finite time, i.e., that they stay positive for positive initial data.
$v(\cdot, 0)$). On the other hand, [Reference Black4] shows that solutions to degenerate chemotaxis systems may not form dead-cores in finite time, i.e., that they stay positive for positive initial data.
As to (1.1), it is known that the support propagates with (at most) finite speed if either ![]() $\Omega = \mathbb{R}$ ([Reference Sugiyama32]) or
$\Omega = \mathbb{R}$ ([Reference Sugiyama32]) or ![]() $\Omega = \mathbb{R}^n$ ([Reference Kim and Yao23]), that the positivity set may be contained in some proper subset of the domain ([Reference Kim and Yao23, Reference Stevens and Winkler30]) and that initial support shrinking is possible if
$\Omega = \mathbb{R}^n$ ([Reference Kim and Yao23]), that the positivity set may be contained in some proper subset of the domain ([Reference Kim and Yao23, Reference Stevens and Winkler30]) and that initial support shrinking is possible if ![]() $\Omega = \mathbb{R}^n$ and
$\Omega = \mathbb{R}^n$ and 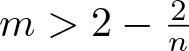 $m \gt 2 - \frac2n$ ([Reference Fischer14]).
$m \gt 2 - \frac2n$ ([Reference Fischer14]).
Main result. Our main result goes beyond these findings and identifies a critical condition distinguishing (for a wide class of initial data) between initial inward and outward motion of the free boundary for radially symmetric solutions of (1.1).
Theorem 1.1. Let ![]() $n \in \mathbb{N}$, R > 0,
$n \in \mathbb{N}$, R > 0, ![]() $\Omega = B_R(0) \subset \mathbb{R}^n$, m > 1 and
$\Omega = B_R(0) \subset \mathbb{R}^n$, m > 1 and ![]() $r_1 \in (0, R)$. Moreover, let
$r_1 \in (0, R)$. Moreover, let ![]() $u_0 \in L^{\infty}(\Omega)$ be radially symmetric and nonnegative a.e. with
$u_0 \in L^{\infty}(\Omega)$ be radially symmetric and nonnegative a.e. with ![]() $\sup (\operatorname{ess}\operatorname{supp} u_0) = r_1$ and set
$\sup (\operatorname{ess}\operatorname{supp} u_0) = r_1$ and set
 \begin{align}
A_{\mathrm{crit}} := \left[ \frac{\int_\Omega u_0 \left(1 - \frac{r_1^n}{R^n}\right) (m-1)}{\omega_n r_1^{n-1}} \right]^\frac{1}{m-1}.
\end{align}
\begin{align}
A_{\mathrm{crit}} := \left[ \frac{\int_\Omega u_0 \left(1 - \frac{r_1^n}{R^n}\right) (m-1)}{\omega_n r_1^{n-1}} \right]^\frac{1}{m-1}.
\end{align} Then there exist ![]() $T_0 \in (0, \infty]$ and a nonnegative, radially symmetric weak solution (u, v) of (1.1) in
$T_0 \in (0, \infty]$ and a nonnegative, radially symmetric weak solution (u, v) of (1.1) in ![]() $\overline \Omega \times [0, T_0)$ in the sense of Definition 2.1 below (which is moreover Hölder continuous if u0 is) such that if
$\overline \Omega \times [0, T_0)$ in the sense of Definition 2.1 below (which is moreover Hölder continuous if u0 is) such that if
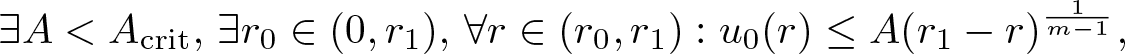 \begin{align}
\exists A \lt A_{\mathrm{crit}},\, \exists r_0 \in (0, r_1),\, \forall r \in (r_0, r_1) : u_0(r) \le A (r_1-r)^\frac{1}{m-1},
\end{align}
\begin{align}
\exists A \lt A_{\mathrm{crit}},\, \exists r_0 \in (0, r_1),\, \forall r \in (r_0, r_1) : u_0(r) \le A (r_1-r)^\frac{1}{m-1},
\end{align} then the spatial support initially shrinks in the sense that there are ![]() $T \in (0,T_0)$ and ζ > 0 with
$T \in (0,T_0)$ and ζ > 0 with
while if
 \begin{align}
\exists A \gt A_{\mathrm{crit}},\, \exists r_0 \in (0, r_1),\, \forall r \in (r_0, r_1) : u_0(r) \ge A (r_1-r)^\frac{1}{m-1},
\end{align}
\begin{align}
\exists A \gt A_{\mathrm{crit}},\, \exists r_0 \in (0, r_1),\, \forall r \in (r_0, r_1) : u_0(r) \ge A (r_1-r)^\frac{1}{m-1},
\end{align} then the spatial support initially expands in the sense that there are ![]() $T \in (0,T_0)$ and ζ > 0 with
$T \in (0,T_0)$ and ζ > 0 with
(Here and throughout the article, we write ![]() $\varphi(|x|)$ for
$\varphi(|x|)$ for ![]() $\varphi(x)$ whenever φ is radially symmetric.)
$\varphi(x)$ whenever φ is radially symmetric.)
Remark 1.2. Since 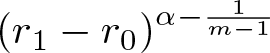 $(r_1-r_0)^{\alpha-\frac{1}{m-1}}$ converges to 0 (respectively,
$(r_1-r_0)^{\alpha-\frac{1}{m-1}}$ converges to 0 (respectively, ![]() $\infty$) as
$\infty$) as ![]() $r_0 \nearrow r_1$ if
$r_0 \nearrow r_1$ if 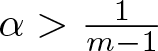 $\alpha \gt \frac{1}{m-1}$ (respectively,
$\alpha \gt \frac{1}{m-1}$ (respectively, 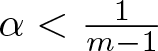 $\alpha \lt \frac{1}{m-1}$), we see that
$\alpha \lt \frac{1}{m-1}$), we see that
 \begin{align}
\exists \alpha \gt \frac{1}{m-1},\, \exists A \gt 0,\, \exists r_0' \in (0, r_1),\, \forall r \in (r_0', r_1) : u_0(r) \le A (r_1 - r)^\alpha
\end{align}
\begin{align}
\exists \alpha \gt \frac{1}{m-1},\, \exists A \gt 0,\, \exists r_0' \in (0, r_1),\, \forall r \in (r_0', r_1) : u_0(r) \le A (r_1 - r)^\alpha
\end{align}and
 \begin{align}
\exists \alpha \lt \frac{1}{m-1},\, \exists A \gt 0,\, \exists r_0' \in (0, r_1),\, \forall r \in (r_0', r_1) : u_0(r) \ge A (r_1 - r)^\alpha
\end{align}
\begin{align}
\exists \alpha \lt \frac{1}{m-1},\, \exists A \gt 0,\, \exists r_0' \in (0, r_1),\, \forall r \in (r_0', r_1) : u_0(r) \ge A (r_1 - r)^\alpha
\end{align}imply (1.4) and (1.6), respectively, and hence initial shrinking and initial expanding, respectively.
Remark 1.3. Our strategy of proof, to be outlined below, necessitates that we limit our attention to radially symmetric settings. Moreover, we note that we can only treat the most outward boundary points of the support; Theorem 1.1 requires ![]() $u_0(x) = 0$ for all
$u_0(x) = 0$ for all ![]() $|x| \ge r_1$.
$|x| \ge r_1$.
Remark 1.4. Let us compare Theorem 1.1 to results regarding the PME (1.2) beyond the fact that the latter are not limited to radially symmetric settings and specific boundary points of the initial positivity set.
(i) The critical exponent
 $\frac{1}{m-1}$ in Theorem 1.1 is smaller than the critical waiting time exponent
$\frac{1}{m-1}$ in Theorem 1.1 is smaller than the critical waiting time exponent  $\frac{2}{m-1}$ for the PME.
$\frac{2}{m-1}$ for the PME.(ii) While the condition (1.9) with
 $\frac{1}{m-1}$ replaced by
$\frac{1}{m-1}$ replaced by  $\frac{2}{m-1}$ implies initial expanding of the support for solutions to the PME, the analogue of (1.8) does not imply initial support shrinking but instead that the support remains constant for some time. That is, the critical exponent for the PME distinguishes between the existence of waiting times and immediate expanding, the critical exponent for (1.1) between shrinking and expanding.
$\frac{2}{m-1}$ implies initial expanding of the support for solutions to the PME, the analogue of (1.8) does not imply initial support shrinking but instead that the support remains constant for some time. That is, the critical exponent for the PME distinguishes between the existence of waiting times and immediate expanding, the critical exponent for (1.1) between shrinking and expanding.(iii) The behaviour at the critical exponent is also different. While for (1.1), Theorem 1.1 shows the existence of a critical parameter
 $A_{\mathrm{crit}}$ and hence in particular that the support of solutions to initial data u 0 with
$A_{\mathrm{crit}}$ and hence in particular that the support of solutions to initial data u 0 with  $u_0(r) \sim (r_1-r)_+^\frac{1}{m-1}$ may shrink or expand depending on the implied constant, all solutions to the PME with initial data
$u_0(r) \sim (r_1-r)_+^\frac{1}{m-1}$ may shrink or expand depending on the implied constant, all solutions to the PME with initial data  $u_0(r) \le A(r_1-r)_+^\frac{2}{m-1}$ exhibit a waiting time phenomenon, regardless of how large A is ([Reference Alikakos1, propsition 4.2]).
$u_0(r) \le A(r_1-r)_+^\frac{2}{m-1}$ exhibit a waiting time phenomenon, regardless of how large A is ([Reference Alikakos1, propsition 4.2]).
Remark 1.5. For the variant of (1.1) posed in the full space and with the second equation replaced by ![]() $-\Delta v = u$, it has been claimed (without detailed proof) in [Reference Fischer14, corollary on p. 1613] that (1.8) implies initial shrinking, provided that
$-\Delta v = u$, it has been claimed (without detailed proof) in [Reference Fischer14, corollary on p. 1613] that (1.8) implies initial shrinking, provided that 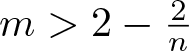 $m \gt 2 - \frac2n$. We again note a few difference to the situation in Theorem 1.1.
$m \gt 2 - \frac2n$. We again note a few difference to the situation in Theorem 1.1.
(i) The results in [Reference Fischer14] also hold in nonradial settings, while we only consider the radially symmetric case. As noted there, the geometric conditions on a point
 $x_0 \in \partial \operatorname{supp} u_0$ required by [Reference Fischer14] are in particular fulfilled whenever x 0 belongs to the boundary of the convex hull of
$x_0 \in \partial \operatorname{supp} u_0$ required by [Reference Fischer14] are in particular fulfilled whenever x 0 belongs to the boundary of the convex hull of  $\operatorname{supp} u_0$. If u 0 is radially symmetric, the latter assumption is equivalent to requiring
$\operatorname{supp} u_0$. If u 0 is radially symmetric, the latter assumption is equivalent to requiring  $u_0(x) = 0$ for all
$u_0(x) = 0$ for all  $|x| \ge |x_0|$, as we do in Theorem 1.1.
$|x| \ge |x_0|$, as we do in Theorem 1.1.(ii) Since [Reference Fischer14] exclusively studies under which conditions shrinking occurs – and not also when expansion happens –, optimality of the exponent
 $\frac{1}{m-1}$ is not obtained there.
$\frac{1}{m-1}$ is not obtained there.(iii) In [Reference Fischer14], shrinking is not claimed for the critical exponent (cf. (43) in [Reference Fischer14]). However, although Theorem 1.1 only covers balls with finite radius, we note that the value
 $A_{\mathrm{crit}}$ in (1.3) converges to a positive, finite number as
$A_{\mathrm{crit}}$ in (1.3) converges to a positive, finite number as  $R \to \infty$. This indicates that also in the full space setting shrinking should be possible for initial data fulfilling
$R \to \infty$. This indicates that also in the full space setting shrinking should be possible for initial data fulfilling  $u_0(r) \sim (r_1-r)_+^\frac{1}{m-1}$ near r 1, and that hence the criterion (43) in [Reference Fischer14] may not be optimal.
$u_0(r) \sim (r_1-r)_+^\frac{1}{m-1}$ near r 1, and that hence the criterion (43) in [Reference Fischer14] may not be optimal.(iv) Finally, we emphasize that, unlike [Reference Fischer14], Theorem 1.1 does not pose any assumption on m beyond the degeneracy condition m > 1; our main result in particular holds in cases where bounded weak solutions cease to exist after finite time (which may be the case if
 $m \lt 2 - \frac2n$, see [Reference Cieślak and Winkler12, Reference Hashira, Ishida and Yokota16]).
$m \lt 2 - \frac2n$, see [Reference Cieślak and Winkler12, Reference Hashira, Ishida and Yokota16]).
Strategy of our proof. The radial symmetry assumption implies that the transformed quantity 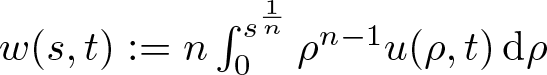 $w(s, t) := n \int_0^{s^\frac1n} \rho^{n-1} u(\rho, t) \,\mathrm{d}\rho$, first introduced in [Reference Jäger and Luckhaus21], solves the scalar equation
$w(s, t) := n \int_0^{s^\frac1n} \rho^{n-1} u(\rho, t) \,\mathrm{d}\rho$, first introduced in [Reference Jäger and Luckhaus21], solves the scalar equation
 \begin{align}
\partial_t w - n^2 s^{2-\frac2n} (\partial_s w)^{m-1} \partial_{ss} w - w \partial_s w + \mu s \partial_s w = 0
\qquad \text{in}\ (0, R^n) \times (0, T_0)
\end{align}
\begin{align}
\partial_t w - n^2 s^{2-\frac2n} (\partial_s w)^{m-1} \partial_{ss} w - w \partial_s w + \mu s \partial_s w = 0
\qquad \text{in}\ (0, R^n) \times (0, T_0)
\end{align} with ![]() $w(0, t) = 0$ and
$w(0, t) = 0$ and ![]() $w(R^n, t) = \mu R^n$ for all
$w(R^n, t) = \mu R^n$ for all ![]() $t \in (0, T)$. Since
$t \in (0, T)$. Since
 \begin{align}
& \big( \sup \{\, r \in (0, R) \mid u(r, t) \gt 0\,\}\big)^n \nonumber\\
& \quad = \inf \{\, s \in (0, R^n) \mid w(s, t) = \mu R^n\,\} =: I_w(t)
\qquad \text{for all}\ t \in (0, T_0),
\end{align}
\begin{align}
& \big( \sup \{\, r \in (0, R) \mid u(r, t) \gt 0\,\}\big)^n \nonumber\\
& \quad = \inf \{\, s \in (0, R^n) \mid w(s, t) = \mu R^n\,\} =: I_w(t)
\qquad \text{for all}\ t \in (0, T_0),
\end{align} the evolution of the most outwards boundary point of the spatial support of u corresponds to monotonicity properties of the infimum ![]() $I_w(t)$ in (1.11). (Potential more inward interface points cannot be characterized in such a way, which is the reason that Theorem 1.1 does not cover them.)
$I_w(t)$ in (1.11). (Potential more inward interface points cannot be characterized in such a way, which is the reason that Theorem 1.1 does not cover them.)
In order to derive suitable estimates for ![]() $I_w(t)$, we shall make use of a comparison principle (cf. Lemma 4.1). For possible sub- and supersolutions, we take the ansatz
$I_w(t)$, we shall make use of a comparison principle (cf. Lemma 4.1). For possible sub- and supersolutions, we take the ansatz
 \begin{align}
w(s,t) := \begin{cases}
\mu R^n - C(r_1^n + \theta t - s)^{\frac{m}{m-1}} & \text{if } s \le r_1^n + \theta t, \\
\mu R^n & \text{if } s \gt r_1^n + \theta t,
\end{cases}
\end{align}
\begin{align}
w(s,t) := \begin{cases}
\mu R^n - C(r_1^n + \theta t - s)^{\frac{m}{m-1}} & \text{if } s \le r_1^n + \theta t, \\
\mu R^n & \text{if } s \gt r_1^n + \theta t,
\end{cases}
\end{align} where θ is negative in the shrinking and positive in the expanding case. (We note that [Reference Stevens and Winkler30] utilizes such comparison functions with θ = 0 to prove persistent localization.) A direct computation reveals that, for ![]() $s \lt r_1^n + \theta t$, the left-hand side in (1.10) equals
$s \lt r_1^n + \theta t$, the left-hand side in (1.10) equals
 \begin{align}
\partial_s w \left[ -\theta + n^2 s^{2-\frac2n} \frac{(Cm)^{m-1}}{(m-1)^m} - w + \mu s\right].
\end{align}
\begin{align}
\partial_s w \left[ -\theta + n^2 s^{2-\frac2n} \frac{(Cm)^{m-1}}{(m-1)^m} - w + \mu s\right].
\end{align} Setting θ = 0 and ![]() $s = r_1^n$, the second factor becomes
$s = r_1^n$, the second factor becomes
 \begin{align}
n^2 r_1^{2n-2} \frac{(Cm)^{m-1}}{(m-1)^m} - \mu (R^n - r_1^n),
\end{align}
\begin{align}
n^2 r_1^{2n-2} \frac{(Cm)^{m-1}}{(m-1)^m} - \mu (R^n - r_1^n),
\end{align} whose sign is determined by the size of C. As long as C is not critical, continuity arguments show that the signs of the quantities in (1.13) and (1.14) are the same as long as ![]() $|\theta|$, t and
$|\theta|$, t and ![]() $r_1^n-s$ are sufficiently small (and
$r_1^n-s$ are sufficiently small (and ![]() $\partial_s w \geq 0$), implying that there are parameters such that the function w in (1.12) is a sub- or supersolution of (1.10) in
$\partial_s w \geq 0$), implying that there are parameters such that the function w in (1.12) is a sub- or supersolution of (1.10) in ![]() $(r_0^n, r_1^n) \times (0, T)$ for r 0 close to r 1 and small T > 0. Since the growth conditions for u 0 in Theorem 1.1 translate to suitable conditions for
$(r_0^n, r_1^n) \times (0, T)$ for r 0 close to r 1 and small T > 0. Since the growth conditions for u 0 in Theorem 1.1 translate to suitable conditions for ![]() $w(\cdot, 0)$ (cf. Lemma 3.1) and as the solution w and the comparison function in (1.12) are correctly ordered at
$w(\cdot, 0)$ (cf. Lemma 3.1) and as the solution w and the comparison function in (1.12) are correctly ordered at ![]() $r_0^n$ (and hence on the whole parabolic boundary) in a small time interval
$r_0^n$ (and hence on the whole parabolic boundary) in a small time interval ![]() $(0, T')$ if they are initially, the comparison principle yields the desired properties of
$(0, T')$ if they are initially, the comparison principle yields the desired properties of ![]() $I_w(t)$.
$I_w(t)$.
As neither the solution w nor the comparison functions above are (known to be) sufficiently regular to allow for rigorous applications of the comparison principle (Lemma 4.1), we instead perform these arguments for solutions ![]() $(u_\varepsilon, v_\varepsilon)$ to approximate, nondegenerate systems. However, this approach introduces some additional challenges; for instance, we need to adjust the comparison functions to account for the fact that the strict maximum principle forces uɛ to become positive immediately.
$(u_\varepsilon, v_\varepsilon)$ to approximate, nondegenerate systems. However, this approach introduces some additional challenges; for instance, we need to adjust the comparison functions to account for the fact that the strict maximum principle forces uɛ to become positive immediately.
Plan of the paper. We recall local existence and approximation theory for (1.1) in ![]() $\S$ 2 and introduce the mass accumulation function in
$\S$ 2 and introduce the mass accumulation function in ![]() $\S$ 3. Section 4 not only contains the key ingredient of our proof, namely the definition of
$\S$ 3. Section 4 not only contains the key ingredient of our proof, namely the definition of ![]() $\underline w$ and
$\underline w$ and ![]() $\overline w$ and the verification of the sub- and supersolution properties, respectively, but also the comparison theorem and the applications to wɛ. Finally, Theorem 1.1 is proven in
$\overline w$ and the verification of the sub- and supersolution properties, respectively, but also the comparison theorem and the applications to wɛ. Finally, Theorem 1.1 is proven in ![]() $\S$ 5.
$\S$ 5.
Notation. We henceforth fix ![]() $n \in \mathbb{N}$, R > 0,
$n \in \mathbb{N}$, R > 0, ![]() $\Omega = B_R(0) \subset \mathbb{R}^n$ and m > 1.
$\Omega = B_R(0) \subset \mathbb{R}^n$ and m > 1.
2. Local existence and convergence to weak solutions
To not unduly duplicate effort, we will largely rely on the weak solution theory for (1.1) presented in [Reference Stevens and Winkler30] for the construction of the solutions discussed in Theorem 1.1. Naturally, this means we will use the same standard notion of weak solution to (1.1) as in the mentioned reference.
Definition 2.1. Let ![]() $T_0 \gt 0$ and let
$T_0 \gt 0$ and let ![]() $u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric with
$u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric with 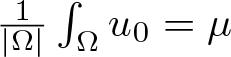 $\frac{1}{|\Omega|} \int_\Omega u_0 = \mu$. We call a pair of radially symmetric functions
$\frac{1}{|\Omega|} \int_\Omega u_0 = \mu$. We call a pair of radially symmetric functions
being such that ![]() $u \ge 0$ a.e. in
$u \ge 0$ a.e. in ![]() $\Omega \times (0, T_0)$ a radial weak solution of (1.1) if
$\Omega \times (0, T_0)$ a radial weak solution of (1.1) if
 \begin{align}
- \int_0^T \int_\Omega u \varphi_t
- \int_\Omega u_0 \varphi(\cdot, 0)
= - \frac1m \int_0^T \int_\Omega \nabla u^m \cdot \nabla \varphi
+ \int_0^T \int_\Omega u \nabla v \cdot \nabla \varphi
\end{align}
\begin{align}
- \int_0^T \int_\Omega u \varphi_t
- \int_\Omega u_0 \varphi(\cdot, 0)
= - \frac1m \int_0^T \int_\Omega \nabla u^m \cdot \nabla \varphi
+ \int_0^T \int_\Omega u \nabla v \cdot \nabla \varphi
\end{align}and
 \begin{align*}
\int_0^T \int_\Omega \nabla v \cdot \nabla \varphi
= - \mu \int_0^T \int_\Omega \varphi
+ \int_0^T \int_\Omega u \varphi
\end{align*}
\begin{align*}
\int_0^T \int_\Omega \nabla v \cdot \nabla \varphi
= - \mu \int_0^T \int_\Omega \varphi
+ \int_0^T \int_\Omega u \varphi
\end{align*} hold for all ![]() $\varphi \in C_c^\infty(\overline \Omega \times [0, T_0))$.
$\varphi \in C_c^\infty(\overline \Omega \times [0, T_0))$.
Remark 2.2. Let ![]() $T_0 \gt 0$, let
$T_0 \gt 0$, let ![]() $u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric and let (u, v) be a radial weak solution of (1.1) in the sense of Definition 2.1.
$u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric and let (u, v) be a radial weak solution of (1.1) in the sense of Definition 2.1.
(1) As also noted in [Reference Stevens and Winkler30, remark after Definition 2.1], the weak formulation (2.1) implies that
 $u_t \in L_{\mathrm{loc}}^2([0, T_0); (W^{1,2}({\Omega}))^\star)$ and hence (after redefining u on a null set of times)
$u_t \in L_{\mathrm{loc}}^2([0, T_0); (W^{1,2}({\Omega}))^\star)$ and hence (after redefining u on a null set of times)  $u \in C^0([0, T_0); L^{2}(\Omega))$.
$u \in C^0([0, T_0); L^{2}(\Omega))$.(2) It has recently been shown in [Reference Black5, corollary 1.9] that u is locally (space-time) Hölder continuous in
 $\overline \Omega \times (0, T_0)$ and that Hölder continuity of u 0 implies that u is Hölder continuous up to t = 0. (For
$\overline \Omega \times (0, T_0)$ and that Hölder continuity of u 0 implies that u is Hölder continuous up to t = 0. (For  $m \le 3$, the same conclusion can be obtained from the classical work [Reference Porzio and Vespri29].)
$m \le 3$, the same conclusion can be obtained from the classical work [Reference Porzio and Vespri29].)
As they will play a crucial role in our coming arguments, let uns now briefly review some of the more intricate details presented in [Reference Stevens and Winkler30] as part of the derivation of such weak solutions. As a matter of fact, the key ingredient used in their construction that we want to utilize is a family of approximate solutions to slightly regularized versions of the system in (1.1), which approach it as the approximation parameter tends to zero and consequently yield our desired solution as their limit. In particular, the central and only change to the system involves mitigation of the nonlinear degeneracy present in the diffusion operator of the first equation in (1.1). This not only enables the following straightforward global classical existence theory in the aforementioned reference but will also provide us with systems and corresponding classical solutions much more amenable to the comparison arguments at the core of our reasoning here.
Lemma 2.3. Let ![]() $u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric. Then we can find
$u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric. Then we can find ![]() $T_0 \gt 0$ such that for all
$T_0 \gt 0$ such that for all ![]() $\varepsilon \in (0, 1)$, a classical solution
$\varepsilon \in (0, 1)$, a classical solution ![]() $(u_\varepsilon, v_\varepsilon)$ of
$(u_\varepsilon, v_\varepsilon)$ of
 \begin{align}
\begin{cases}
u_{\varepsilon t} = \nabla \cdot ( (u_\varepsilon + \varepsilon)^{m-1} \nabla u_\varepsilon - u_\varepsilon \nabla v_\varepsilon) & \text{in}\ \Omega \times (0, T_0), \\
0 = \Delta v_\varepsilon - \mu + u_\varepsilon, \quad \mu = \frac{1}{|\Omega|} \int_\Omega u_0, & \text{in}\ \Omega \times (0, T_0), \\
\partial_\nu u_\varepsilon = \partial_\nu v_\varepsilon = 0 & \text{on}\ \partial\Omega \times (0, T_0), \\
u_\varepsilon(\cdot, 0) = u_0 & \text{in}\ \Omega
\end{cases}
\end{align}
\begin{align}
\begin{cases}
u_{\varepsilon t} = \nabla \cdot ( (u_\varepsilon + \varepsilon)^{m-1} \nabla u_\varepsilon - u_\varepsilon \nabla v_\varepsilon) & \text{in}\ \Omega \times (0, T_0), \\
0 = \Delta v_\varepsilon - \mu + u_\varepsilon, \quad \mu = \frac{1}{|\Omega|} \int_\Omega u_0, & \text{in}\ \Omega \times (0, T_0), \\
\partial_\nu u_\varepsilon = \partial_\nu v_\varepsilon = 0 & \text{on}\ \partial\Omega \times (0, T_0), \\
u_\varepsilon(\cdot, 0) = u_0 & \text{in}\ \Omega
\end{cases}
\end{align}satisfying
 \begin{align*}
u_\varepsilon \in C^{2, 1}(\overline \Omega \times (0, T_0)) \cap C^0([0, T_0); L^{1}(\Omega)), \quad
v_\varepsilon \in C^{2, 0}(\overline \Omega \times (0, T_0))
\quad \text{and} \quad
\int_\Omega v_\varepsilon = 0
\end{align*}
\begin{align*}
u_\varepsilon \in C^{2, 1}(\overline \Omega \times (0, T_0)) \cap C^0([0, T_0); L^{1}(\Omega)), \quad
v_\varepsilon \in C^{2, 0}(\overline \Omega \times (0, T_0))
\quad \text{and} \quad
\int_\Omega v_\varepsilon = 0
\end{align*} exists, which is moreover such that ![]() $u_\varepsilon(\cdot, t)$ and
$u_\varepsilon(\cdot, t)$ and ![]() $v_\varepsilon(\cdot, t)$ are radially symmetric for all
$v_\varepsilon(\cdot, t)$ are radially symmetric for all ![]() $t \in (0, T_0)$ and that
$t \in (0, T_0)$ and that
 \begin{align}
0 \lt u_\varepsilon \leq \|u_0\|_{L^{\infty}({\Omega})} + 1
\qquad \text{in}\ \overline \Omega \times (0, T_0).
\end{align}
\begin{align}
0 \lt u_\varepsilon \leq \|u_0\|_{L^{\infty}({\Omega})} + 1
\qquad \text{in}\ \overline \Omega \times (0, T_0).
\end{align} for all ![]() $\varepsilon \in (0, 1)$.
$\varepsilon \in (0, 1)$.
Proof. See [Reference Stevens and Winkler30, Lemma 2.1].
Using a series of testing procedures, sufficient convergence properties are then derived in [Reference Stevens and Winkler30] for the family of approximate solutions constructed in Lemma 2.3 to ensure that the weak solution properties they enjoy (due to them being classical solutions) survive the limit process in an appropriate fashion.
Lemma 2.4. Let ![]() $u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric and let T0 and
$u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric and let T0 and ![]() $(u_\varepsilon, v_\varepsilon)_{\varepsilon \in (0, 1)}$ be as given by Lemma 2.3. Then there exist a null sequence
$(u_\varepsilon, v_\varepsilon)_{\varepsilon \in (0, 1)}$ be as given by Lemma 2.3. Then there exist a null sequence ![]() $(\varepsilon_j)_{j \in \mathbb{N}} \subset (0, 1)$ and a radial weak solution (u, v) of (1.1) in the sense of Definition 2.1 such that
$(\varepsilon_j)_{j \in \mathbb{N}} \subset (0, 1)$ and a radial weak solution (u, v) of (1.1) in the sense of Definition 2.1 such that
Proof. This has been shown in [Reference Stevens and Winkler30, Lemma 2.3].
Lastly, we prove a uniform continuity result in t = 0 to complement the other solution properties already laid out above by another testing procedure. This will later help us to localize our central comparison arguments around the boundary of the support of the initial data.
Lemma 2.5. Let ![]() $u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric and let T0 and
$u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric and let T0 and ![]() $(u_\varepsilon, v_\varepsilon)_{\varepsilon \in (0, 1)}$ be as given by Lemma 2.3. Then for every
$(u_\varepsilon, v_\varepsilon)_{\varepsilon \in (0, 1)}$ be as given by Lemma 2.3. Then for every ![]() $r \in (0, R)$ and δ > 0, there exists
$r \in (0, R)$ and δ > 0, there exists ![]() $t_0 \in (0,T_0)$ such that
$t_0 \in (0,T_0)$ such that
 \begin{align*}
\left| \int_{B_r(0)} u_0 - \int_{B_r(0)} u_\varepsilon(\cdot, t) \right| \leq \delta
\end{align*}
\begin{align*}
\left| \int_{B_r(0)} u_0 - \int_{B_r(0)} u_\varepsilon(\cdot, t) \right| \leq \delta
\end{align*} for all ![]() $t\in(0,t_0)$ and
$t\in(0,t_0)$ and ![]() $\varepsilon \in (0,1)$.
$\varepsilon \in (0,1)$.
Proof. Using a similar testing-based approach to [Reference Stevens and Winkler30, Lemma 2.3] combined with the fundamental theorem of calculus, we can immediately see that
 \begin{align*}
& \left| \int_\Omega u_0\varphi - \int_\Omega u_\varepsilon(\cdot, t) \varphi \right| = \left| \int_0^t \int_\Omega u_{\varepsilon t} \varphi \right| \\
& \quad \leq \int_0^t \left( \tfrac{|\Omega|}{m} \|u_\varepsilon + 1\|^m_{L^{\infty}(\Omega)} \|\Delta \varphi\|_{L^{\infty}(\Omega)} + \|u_\varepsilon\|_{L^{\infty}(\Omega)} \|\nabla v_\varepsilon\|_{L^{1}(\Omega)} \|\nabla \varphi\|_{L^{\infty}(\Omega)} \right)
\end{align*}
\begin{align*}
& \left| \int_\Omega u_0\varphi - \int_\Omega u_\varepsilon(\cdot, t) \varphi \right| = \left| \int_0^t \int_\Omega u_{\varepsilon t} \varphi \right| \\
& \quad \leq \int_0^t \left( \tfrac{|\Omega|}{m} \|u_\varepsilon + 1\|^m_{L^{\infty}(\Omega)} \|\Delta \varphi\|_{L^{\infty}(\Omega)} + \|u_\varepsilon\|_{L^{\infty}(\Omega)} \|\nabla v_\varepsilon\|_{L^{1}(\Omega)} \|\nabla \varphi\|_{L^{\infty}(\Omega)} \right)
\end{align*} for all ![]() $\varphi \in C^\infty_c(\Omega)$,
$\varphi \in C^\infty_c(\Omega)$, ![]() $t\in(0,T_0)$ and
$t\in(0,T_0)$ and ![]() $\varepsilon \in (0,1)$. By for instance testing the second equation in (2.2) with vɛ to gain a uniform-in-time gradient bound for vɛ combined with the uniform bound for uɛ found in (2.3), we gain
$\varepsilon \in (0,1)$. By for instance testing the second equation in (2.2) with vɛ to gain a uniform-in-time gradient bound for vɛ combined with the uniform bound for uɛ found in (2.3), we gain ![]() $C \equiv C(\|u_0\|_{L^{\infty}(\Omega)}) \gt 0$ such that
$C \equiv C(\|u_0\|_{L^{\infty}(\Omega)}) \gt 0$ such that
 \begin{align}
\left| \int_\Omega u_0\varphi - \int_\Omega u_\varepsilon(\cdot, t) \varphi \right| \leq C (\|\nabla \varphi\|_{L^{\infty}(\Omega)} + \|\Delta \varphi\|_{L^{\infty}(\Omega)}) t
\end{align}
\begin{align}
\left| \int_\Omega u_0\varphi - \int_\Omega u_\varepsilon(\cdot, t) \varphi \right| \leq C (\|\nabla \varphi\|_{L^{\infty}(\Omega)} + \|\Delta \varphi\|_{L^{\infty}(\Omega)}) t
\end{align} for all ![]() $\varphi \in C^\infty_c(\Omega)$,
$\varphi \in C^\infty_c(\Omega)$, ![]() $t\in(0,T_0)$ and
$t\in(0,T_0)$ and ![]() $\varepsilon \in (0,1)$.
$\varepsilon \in (0,1)$.
We now fix ![]() $r \in (0, R)$ and δ > 0. We then choose a cutoff function
$r \in (0, R)$ and δ > 0. We then choose a cutoff function ![]() $\varphi \in C_c^\infty(\Omega)$ with
$\varphi \in C_c^\infty(\Omega)$ with ![]() $\varphi \equiv 1$ on
$\varphi \equiv 1$ on ![]() $B_r(0)$ and
$B_r(0)$ and 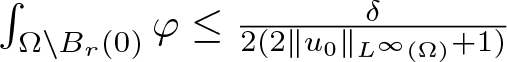 $\int_{\Omega\setminus B_r(0)} \varphi \leq \frac{\delta}{2(2\|u_0\|_{L^{\infty}(\Omega)}+1)}$. Using (2.5), we then fix
$\int_{\Omega\setminus B_r(0)} \varphi \leq \frac{\delta}{2(2\|u_0\|_{L^{\infty}(\Omega)}+1)}$. Using (2.5), we then fix ![]() $t_0 \in (0,T)$ such that
$t_0 \in (0,T)$ such that
 \begin{align*}
\left| \int_\Omega u_0\varphi - \int_\Omega u_\varepsilon(\cdot, t) \varphi \right| \leq \frac{\delta}{2}
\end{align*}
\begin{align*}
\left| \int_\Omega u_0\varphi - \int_\Omega u_\varepsilon(\cdot, t) \varphi \right| \leq \frac{\delta}{2}
\end{align*} for all ![]() $t\in(0,t_0)$ and
$t\in(0,t_0)$ and ![]() $\varepsilon \in (0,1)$. Combining these choices for φ and t 0 with (2.3), we then gain
$\varepsilon \in (0,1)$. Combining these choices for φ and t 0 with (2.3), we then gain
 \begin{align*}
\left| \int_{B_r(0)} u_0 - \int_{B_r(0)} u_\varepsilon(\cdot, t) \right| &= \left| \int_{B_r(0)} u_0\varphi - \int_{B_r(0)} u_\varepsilon(\cdot, t)\varphi \right| \\
&\leq \left| \int_{\Omega} u_0\varphi - \int_{\Omega} u_\varepsilon(\cdot, t)\varphi \right| + \int_{\Omega\setminus B_r(0)} |u_0 - u_\varepsilon(\cdot, t)| \varphi \\
&\leq \frac{\delta}{2} + (2\|u_0\|_{L^{\infty}(\Omega)}+1)\int_{\Omega\setminus B_r(0)}\varphi \leq \delta
\end{align*}
\begin{align*}
\left| \int_{B_r(0)} u_0 - \int_{B_r(0)} u_\varepsilon(\cdot, t) \right| &= \left| \int_{B_r(0)} u_0\varphi - \int_{B_r(0)} u_\varepsilon(\cdot, t)\varphi \right| \\
&\leq \left| \int_{\Omega} u_0\varphi - \int_{\Omega} u_\varepsilon(\cdot, t)\varphi \right| + \int_{\Omega\setminus B_r(0)} |u_0 - u_\varepsilon(\cdot, t)| \varphi \\
&\leq \frac{\delta}{2} + (2\|u_0\|_{L^{\infty}(\Omega)}+1)\int_{\Omega\setminus B_r(0)}\varphi \leq \delta
\end{align*} for all ![]() $t\in(0,t_0)$ and
$t\in(0,t_0)$ and ![]() $\varepsilon \in (0,1)$. This completes the proof.
$\varepsilon \in (0,1)$. This completes the proof.
For the remainder of the paper, we now fix a nonnegative, radially symmetric ![]() $u_0 \in L^{\infty}({\Omega})$ and set
$u_0 \in L^{\infty}({\Omega})$ and set 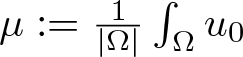 $\mu := \frac{1}{|\Omega|} \int_\Omega u_0$. Moreover, we fix the family of approximate solutions
$\mu := \frac{1}{|\Omega|} \int_\Omega u_0$. Moreover, we fix the family of approximate solutions ![]() $(u_\varepsilon, v_\varepsilon)_{\varepsilon \in (0,1)}$ with uniform existence time
$(u_\varepsilon, v_\varepsilon)_{\varepsilon \in (0,1)}$ with uniform existence time ![]() $T_0 \gt 0$ constructed in Lemma 2.3 as well as the limit solution (u, v) found in Lemma 2.4.
$T_0 \gt 0$ constructed in Lemma 2.3 as well as the limit solution (u, v) found in Lemma 2.4.
3. Mass accumulation functions
As pioneered in [Reference Jäger and Luckhaus21] for systems simplified in a similar fashion to (1.1) and also considered in radial settings, we will from now on mostly focus on an derived quantity instead of the functions uɛ and vɛ themselves. Namely, we consider the mass accumulation functions
 \begin{align*}
w_\varepsilon(s,t) := n \int_0^{s^\frac1n} \rho^{n-1} u_\varepsilon(\rho, t) \,\mathrm{d}\rho \quad \text{and\, similarly}\quad\!\! w(s,t) := n \int_0^{s^\frac1n} \rho^{n-1} u(\rho, t) \,\mathrm{d}\rho
\end{align*}
\begin{align*}
w_\varepsilon(s,t) := n \int_0^{s^\frac1n} \rho^{n-1} u_\varepsilon(\rho, t) \,\mathrm{d}\rho \quad \text{and\, similarly}\quad\!\! w(s,t) := n \int_0^{s^\frac1n} \rho^{n-1} u(\rho, t) \,\mathrm{d}\rho
\end{align*} for all ![]() $(s,t) \in [0,R^n]\times[0,T_0]$ and
$(s,t) \in [0,R^n]\times[0,T_0]$ and ![]() $\varepsilon \in (0,1)$. Making use of radial symmetry, a straightforward computation then yields that wɛ solves the parabolic differential equation
$\varepsilon \in (0,1)$. Making use of radial symmetry, a straightforward computation then yields that wɛ solves the parabolic differential equation
 \begin{align}
0 = \mathcal{P}_\varepsilon w_\varepsilon = \partial_t w_\varepsilon
- n^2 s^{2-\frac{2}{n}} (\partial_s w_\varepsilon + \varepsilon)^{m-1} \partial_{ss} w_\varepsilon
- w_\varepsilon \partial_s w_\varepsilon
+ \mu s \partial_s w_\varepsilon
\end{align}
\begin{align}
0 = \mathcal{P}_\varepsilon w_\varepsilon = \partial_t w_\varepsilon
- n^2 s^{2-\frac{2}{n}} (\partial_s w_\varepsilon + \varepsilon)^{m-1} \partial_{ss} w_\varepsilon
- w_\varepsilon \partial_s w_\varepsilon
+ \mu s \partial_s w_\varepsilon
\end{align} on ![]() $[0,R^n]\times[0,T_0]$ with initial data
$[0,R^n]\times[0,T_0]$ with initial data  $w_0(s) := n \int_0^{s^\frac1n} \rho^{n-1} u_0(\rho) \,\mathrm{d}\rho$. Additionally, it is immediately obvious from the nonnegativity of uɛ as well as the mass conservation properties of (2.2) that
$w_0(s) := n \int_0^{s^\frac1n} \rho^{n-1} u_0(\rho) \,\mathrm{d}\rho$. Additionally, it is immediately obvious from the nonnegativity of uɛ as well as the mass conservation properties of (2.2) that ![]() $w_\varepsilon(\cdot, t)$ is monotonically increasing and
$w_\varepsilon(\cdot, t)$ is monotonically increasing and ![]() $w_\varepsilon(0, t) = 0$ as well as
$w_\varepsilon(0, t) = 0$ as well as ![]() $w_\varepsilon(R^n, t) = \mu R^n$ for all
$w_\varepsilon(R^n, t) = \mu R^n$ for all ![]() $t\in[0,T_0]$.
$t\in[0,T_0]$.
Let us now further note that the a.e. pointwise convergence properties of the family ![]() $(u_\varepsilon)_{\varepsilon\in(0,1)}$ toward u in (2.4) translate in a sensible way to these newly introduced quantities. In fact along the null sequence
$(u_\varepsilon)_{\varepsilon\in(0,1)}$ toward u in (2.4) translate in a sensible way to these newly introduced quantities. In fact along the null sequence ![]() $(\varepsilon_j)_{j \in \mathbb{N}}$ constructed in Lemma 2.4, we gain that
$(\varepsilon_j)_{j \in \mathbb{N}}$ constructed in Lemma 2.4, we gain that
for all ![]() $s\in[0, R^n]$ and a.e.
$s\in[0, R^n]$ and a.e. ![]() $t\in[0,T_0]$ by an application of Lebesgue’s theorem, which is possible due to the uniform bound seen in (2.3). Notably, this directly implies that
$t\in[0,T_0]$ by an application of Lebesgue’s theorem, which is possible due to the uniform bound seen in (2.3). Notably, this directly implies that
for all ![]() $s\in[0, R^n]$ and a.e.
$s\in[0, R^n]$ and a.e. ![]() $t\in[0,T_0]$ due to these property uniformly holding for the approximate functions wɛ.
$t\in[0,T_0]$ due to these property uniformly holding for the approximate functions wɛ.
Next, we investigate how our central initial data conditions (1.4) and (1.6) in Theorem 1.1 translate from u 0 to its mass accumulation counterpart w 0.
Lemma 3.1. Let ![]() $u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric with
$u_0 \in L^{\infty}({\Omega})$ be nonnegative and radially symmetric with ![]() $\operatorname{ess}\operatorname{supp} u_0 \subseteq \overline{B_{r_1}(0)}$ for some
$\operatorname{ess}\operatorname{supp} u_0 \subseteq \overline{B_{r_1}(0)}$ for some ![]() $r_1 \in (0, R)$. If (1.4) holds for some A > 0 and
$r_1 \in (0, R)$. If (1.4) holds for some A > 0 and ![]() $r_0 \in (0,r_1)$, then
$r_0 \in (0,r_1)$, then
 \begin{align}
w_0(s) \geq \mu R^n - \frac{A n^{-\frac{1}{m-1}} r_0^{-\frac{(n-1)m}{m-1}} r_1^{n-1} (m-1)}{m} (r_1^n - s)^\frac{m}{m-1}
\end{align}
\begin{align}
w_0(s) \geq \mu R^n - \frac{A n^{-\frac{1}{m-1}} r_0^{-\frac{(n-1)m}{m-1}} r_1^{n-1} (m-1)}{m} (r_1^n - s)^\frac{m}{m-1}
\end{align} for all s ![]() $\in (r_0^n, r_1^n)$.
$\in (r_0^n, r_1^n)$.
Similarly, if (1.6) holds for some A > 0 and ![]() $r_0 \in (0,r_1)$, then
$r_0 \in (0,r_1)$, then
 \begin{align}
w_0(s) \leq \mu R^n - \frac{A n^{-\frac{1}{m-1}} r_1^{-\frac{(n-1)m}{m-1}} r_0^{n-1} (m-1)}{m} (r_1^n - s)^\frac{m}{m-1}
\end{align}
\begin{align}
w_0(s) \leq \mu R^n - \frac{A n^{-\frac{1}{m-1}} r_1^{-\frac{(n-1)m}{m-1}} r_0^{n-1} (m-1)}{m} (r_1^n - s)^\frac{m}{m-1}
\end{align} for all s ![]() $\in (r_0^n, r_1^n)$.
$\in (r_0^n, r_1^n)$.
Proof. Assuming that (1.4) holds for some A > 0 and ![]() $r_0 \in (0,r_1)$, a direct computation yields
$r_0 \in (0,r_1)$, a direct computation yields
 \begin{align*}
w_0(s)
&= n \int_0^{s^\frac1n} \rho^{n-1} u_0(\rho) \,\mathrm{d}\rho
= n \int_0^{R} \rho^{n-1} u_0(\rho) \,\mathrm{d}\rho
- n \int_{s^\frac1n}^{r_1} \rho^{n-1} u_0(\rho) \,\mathrm{d}\rho \\
&\ge \mu R^n - A n r_1^{n-1} \int_{s^\frac1n}^{r_1} (r_1 - \rho)^\frac{1}{m-1} \,\mathrm{d}\rho \\
&= \mu R^n - \frac{A n r_1^{n-1}(m-1)}{m} ((r_1^n)^\frac1n - s^\frac1n)^{\frac{m}{m-1}} \\
&\ge \mu R^n - \frac{A n^{-\frac{1}{m-1}}r_0^{-\frac{(n-1)m}{m-1}} r_1^{n-1} (m-1)}{m} (r_1^n - s)^{\frac{m}{m-1}}
\qquad \text{for all}\ s \in (r_0^n, r_1^n),
\end{align*}
\begin{align*}
w_0(s)
&= n \int_0^{s^\frac1n} \rho^{n-1} u_0(\rho) \,\mathrm{d}\rho
= n \int_0^{R} \rho^{n-1} u_0(\rho) \,\mathrm{d}\rho
- n \int_{s^\frac1n}^{r_1} \rho^{n-1} u_0(\rho) \,\mathrm{d}\rho \\
&\ge \mu R^n - A n r_1^{n-1} \int_{s^\frac1n}^{r_1} (r_1 - \rho)^\frac{1}{m-1} \,\mathrm{d}\rho \\
&= \mu R^n - \frac{A n r_1^{n-1}(m-1)}{m} ((r_1^n)^\frac1n - s^\frac1n)^{\frac{m}{m-1}} \\
&\ge \mu R^n - \frac{A n^{-\frac{1}{m-1}}r_0^{-\frac{(n-1)m}{m-1}} r_1^{n-1} (m-1)}{m} (r_1^n - s)^{\frac{m}{m-1}}
\qquad \text{for all}\ s \in (r_0^n, r_1^n),
\end{align*} where in the last step we applied the mean value theorem, which for all ![]() $0 \lt a \lt b$ asserts the existence of
$0 \lt a \lt b$ asserts the existence of ![]() $\xi \in (a, b)$ with
$\xi \in (a, b)$ with 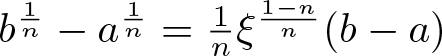 $b^\frac1n-a^\frac1n = \frac1n \xi^{\frac{1-n}{n}} (b-a)$.
$b^\frac1n-a^\frac1n = \frac1n \xi^{\frac{1-n}{n}} (b-a)$.
If on the other hand (1.6) holds for some A > 0 and ![]() $r_0 \in (0,r_1)$, (3.5) is obtained by an analogous argument.
$r_0 \in (0,r_1)$, (3.5) is obtained by an analogous argument.
4. Comparison argument
Our aim now is to find a (potentially short) time ![]() $T \in (0,T_0)$ and constants
$T \in (0,T_0)$ and constants ![]() $C, \theta \gt 0$ such that w stays above or below functions of the general prototype
$C, \theta \gt 0$ such that w stays above or below functions of the general prototype
 \begin{align}
(s,t) \mapsto \begin{cases}
\mu R^n- C (r_1^n \pm \theta t - s)^{\frac{m}{m-1}}& \text{if } s \lt r_1^n \pm \theta t, \\
\mu R^n &\text{if } s \geq r_1^n \pm \theta t
\end{cases}
\end{align}
\begin{align}
(s,t) \mapsto \begin{cases}
\mu R^n- C (r_1^n \pm \theta t - s)^{\frac{m}{m-1}}& \text{if } s \lt r_1^n \pm \theta t, \\
\mu R^n &\text{if } s \geq r_1^n \pm \theta t
\end{cases}
\end{align} on ![]() $(r_0^n, R^n)$ under the assumption that such an ordering already holds true at t = 0 for a constant C > 0 either larger or smaller (depending on the case) than the critical constant
$(r_0^n, R^n)$ under the assumption that such an ordering already holds true at t = 0 for a constant C > 0 either larger or smaller (depending on the case) than the critical constant
 \begin{align}
C_{\mathrm{crit}}(r_1) := \frac{m-1}{m}\left(\frac{\mu(R^n - r_1^n)(m-1)}{r_1^{2n - 2} n^2}\right)^\frac{1}{m-1}.
\end{align}
\begin{align}
C_{\mathrm{crit}}(r_1) := \frac{m-1}{m}\left(\frac{\mu(R^n - r_1^n)(m-1)}{r_1^{2n - 2} n^2}\right)^\frac{1}{m-1}.
\end{align}This shall be achieved by comparing the approximate solutions wɛ to suitably adapted versions of (4.1), which, however, are nonsmooth, so that we need to ensure the applicability of a suitable comparison principle. To this end, we will utilize the following Lemma which is built on the more general comparison result seen in [Reference Bellomo and Winkler3, Lemma 5.1]. (We note that the comparison theorem presented in [Reference Stevens and Winkler30, Lemma 2.2] is also based on [Reference Bellomo and Winkler3, Lemma 5.1], but requires the comparison functions to be strictly increasing and is hence not suitable for all of our purposes.)
Lemma 4.1. Let ![]() $\varepsilon \in (0,1)$,
$\varepsilon \in (0,1)$, ![]() $a, b \in \mathbb{R}$ with a < b and T > 0, and suppose that
$a, b \in \mathbb{R}$ with a < b and T > 0, and suppose that ![]() $\underline w,\, \overline w \in C^0([a, b] \times [0, T)) \cap C^1((a,b) \times (0, T))$ with
$\underline w,\, \overline w \in C^0([a, b] \times [0, T)) \cap C^1((a,b) \times (0, T))$ with ![]() $\partial_s \underline w,\, \partial_s \overline w \in L_{\mathrm{loc}}^\infty([a,b] \times [0, T))$ satisfy
$\partial_s \underline w,\, \partial_s \overline w \in L_{\mathrm{loc}}^\infty([a,b] \times [0, T))$ satisfy
and
 \begin{align}
\underline w(\cdot, t),\, \overline w(\cdot, t) \in W_{\mathrm{loc}}^{2, \infty}((a, b)) \qquad \text{for all}\ t \in (0, T).
\end{align}
\begin{align}
\underline w(\cdot, t),\, \overline w(\cdot, t) \in W_{\mathrm{loc}}^{2, \infty}((a, b)) \qquad \text{for all}\ t \in (0, T).
\end{align}If
then
Proof. To put our case into the framework of the more general comparison principle presented in [Reference Bellomo and Winkler3, Lemma 5.1], we let
 \begin{align*}
\overline W(s,t) := \overline w\left( \tfrac{b-a}{b}s + a, t\right) + \varepsilon \tfrac{b-a}{b} s \quad \text{and}\quad\!\! \underline W(s,t) := \underline w\left( \tfrac{b-a}{b}s + a, t\right) + \varepsilon \tfrac{b-a}{b} s
\end{align*}
\begin{align*}
\overline W(s,t) := \overline w\left( \tfrac{b-a}{b}s + a, t\right) + \varepsilon \tfrac{b-a}{b} s \quad \text{and}\quad\!\! \underline W(s,t) := \underline w\left( \tfrac{b-a}{b}s + a, t\right) + \varepsilon \tfrac{b-a}{b} s
\end{align*} for all ![]() $(s, t) \in [0,L]\times[0,T)$ with
$(s, t) \in [0,L]\times[0,T)$ with ![]() $L := b$. As we have only modified the original functions
$L := b$. As we have only modified the original functions ![]() $\overline w$,
$\overline w$, ![]() $\underline w$ in a linear fashion, the new functions
$\underline w$ in a linear fashion, the new functions ![]() $\overline W$,
$\overline W$, ![]() $\underline W$ naturally retain all of our assumed regularity properties as well as the proper ordering at the parabolic boundary of
$\underline W$ naturally retain all of our assumed regularity properties as well as the proper ordering at the parabolic boundary of ![]() $[0,L]\times[0,T)$ due to (4.7) as well as (4.8). Due to (4.3) and a < b, it is further directly evident that
$[0,L]\times[0,T)$ due to (4.7) as well as (4.8). Due to (4.3) and a < b, it is further directly evident that ![]() $\partial_s \overline W \gt 0$ and
$\partial_s \overline W \gt 0$ and ![]() $\partial_s \underline W \gt 0$ in
$\partial_s \underline W \gt 0$ in ![]() $(0,L)\times(0,T)$. Finally due to (4.5) and (4.6), it follows by direct computation that
$(0,L)\times(0,T)$. Finally due to (4.5) and (4.6), it follows by direct computation that
for a.e. ![]() $s \in (0,L)$ and all
$s \in (0,L)$ and all ![]() $t\in(0,T)$ with
$t\in(0,T)$ with
 \begin{align*}
\Phi(s,t,y_0,y_1,y_2) & := n^2 \left( \tfrac{b-a}{b}s + a \right)^{2-\frac{2}{n}}\left(\tfrac{b}{b-a}\right)^{m+1} y_1^{m-1} y_2 \\
& \quad + \left(y_0 - \varepsilon \tfrac{b-a}{b} s - \mu(\tfrac{b-a}{b}s + a)\right)(\tfrac{b}{b-a}y_1 - \varepsilon)
\end{align*}
\begin{align*}
\Phi(s,t,y_0,y_1,y_2) & := n^2 \left( \tfrac{b-a}{b}s + a \right)^{2-\frac{2}{n}}\left(\tfrac{b}{b-a}\right)^{m+1} y_1^{m-1} y_2 \\
& \quad + \left(y_0 - \varepsilon \tfrac{b-a}{b} s - \mu(\tfrac{b-a}{b}s + a)\right)(\tfrac{b}{b-a}y_1 - \varepsilon)
\end{align*} for all ![]() $(s,t,y_0,y_1,y_2) \in G:= (0,L)\times(0,T)\times\mathbb{R}\times(0,\infty)\times\mathbb{R}$. Moreover, we see that
$(s,t,y_0,y_1,y_2) \in G:= (0,L)\times(0,T)\times\mathbb{R}\times(0,\infty)\times\mathbb{R}$. Moreover, we see that
 \begin{align*}
\frac{\partial \Phi}{\partial y_2}(s,t,y_0,y_1,y_2) \geq 0 \quad \text{and}\!\quad \left|\frac{\partial \Phi}{\partial y_0}(s,t,y_0,y_1,y_2)\right| \leq \frac{b}{b-a}y_1 + 1
\end{align*}
\begin{align*}
\frac{\partial \Phi}{\partial y_2}(s,t,y_0,y_1,y_2) \geq 0 \quad \text{and}\!\quad \left|\frac{\partial \Phi}{\partial y_0}(s,t,y_0,y_1,y_2)\right| \leq \frac{b}{b-a}y_1 + 1
\end{align*} for all ![]() $(s,t,y_0,y_1,y_2) \in G$ as well as that
$(s,t,y_0,y_1,y_2) \in G$ as well as that 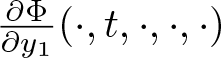 $\frac{\partial \Phi}{\partial y_1}(\cdot, t, \cdot, \cdot, \cdot)$ is bounded on every compact set in
$\frac{\partial \Phi}{\partial y_1}(\cdot, t, \cdot, \cdot, \cdot)$ is bounded on every compact set in ![]() $(0,L)\times\mathbb{R}\times(0,\infty)\times \mathbb{R}$ for all
$(0,L)\times\mathbb{R}\times(0,\infty)\times \mathbb{R}$ for all ![]() $t\in(0,T)$. Thus, our desired ordering property for
$t\in(0,T)$. Thus, our desired ordering property for ![]() $\overline W$ and
$\overline W$ and ![]() $\underline W$ on
$\underline W$ on ![]() $(0,L)\times(0,T)$ and therefore (4.9) follow from [Reference Bellomo and Winkler3, proof of Lemma 5.1] which, as already observed in [Reference Stevens and Winkler30, directly before Lemma 2.2], implies the conclusion of [Reference Bellomo and Winkler3, Lemma 5.1] also for the slightly weaker regularity conditions on
$(0,L)\times(0,T)$ and therefore (4.9) follow from [Reference Bellomo and Winkler3, proof of Lemma 5.1] which, as already observed in [Reference Stevens and Winkler30, directly before Lemma 2.2], implies the conclusion of [Reference Bellomo and Winkler3, Lemma 5.1] also for the slightly weaker regularity conditions on ![]() $\underline w$ and
$\underline w$ and ![]() $\overline w$ imposed here.
$\overline w$ imposed here.
4.1. Case of support shrinking
Having now established the comparison principle at the center of this section, we start treating the support shrinking case by showing that w lies above a function of the type seen in (4.1) with a negative coefficient for θ under an appropriate assumption at t = 0. This will then imply ![]() $w(s, t) = \mu R^n$ and hence
$w(s, t) = \mu R^n$ and hence 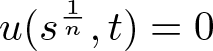 $u(s^\frac1n, t) = 0$ for a.e. sufficiently small time t and
$u(s^\frac1n, t) = 0$ for a.e. sufficiently small time t and ![]() $s \ge r_1^n - \theta t$; that is, that the support indeed initially shrinks.
$s \ge r_1^n - \theta t$; that is, that the support indeed initially shrinks.
As already mentioned previously, our first step in this endeavour is to construct a family of subsolutions for the approximate functions wɛ by modifying the prototypical function in (4.1) to make it compatible with the regularized equation (3.1). We first note that due to the diffusion operator in our regularized system (2.2) no longer being degenerate, our approximate solutions uɛ become immediately positive. This in turn means that ![]() $w_\varepsilon(\cdot, t)$ is strictly monotonically increasing. As further
$w_\varepsilon(\cdot, t)$ is strictly monotonically increasing. As further ![]() $w_\varepsilon(R^n, t) = \mu R^n$ for all
$w_\varepsilon(R^n, t) = \mu R^n$ for all ![]() $t\in[0,T_0)$, we will thus need to replace the constant extension in (4.1) by something increasing in a similar fashion to have any chance for the resulting function to be a subsolution. In fact for our approximate subsolutions, we will extend the left part of (4.1) by a linearly increasing function by moving the extension point slightly to the left of
$t\in[0,T_0)$, we will thus need to replace the constant extension in (4.1) by something increasing in a similar fashion to have any chance for the resulting function to be a subsolution. In fact for our approximate subsolutions, we will extend the left part of (4.1) by a linearly increasing function by moving the extension point slightly to the left of ![]() $r_1^n - \theta t$ where the first derivate is still positive. We then move the resulting function slightly down to ensure that the right boundary value is still sufficiently close to
$r_1^n - \theta t$ where the first derivate is still positive. We then move the resulting function slightly down to ensure that the right boundary value is still sufficiently close to ![]() $\mu R^n$ on small time scales. Conveniently, this modification also allows us to work around the potential singularity present in the second derivative of (4.1) at
$\mu R^n$ on small time scales. Conveniently, this modification also allows us to work around the potential singularity present in the second derivative of (4.1) at ![]() $r_1^n - \theta t$. The remaining modifications and parameter choices are mostly in service of allowing us to use the optimal value for
$r_1^n - \theta t$. The remaining modifications and parameter choices are mostly in service of allowing us to use the optimal value for ![]() $C_{\mathrm{crit}}$.
$C_{\mathrm{crit}}$.
Lemma 4.2. Let ![]() $r_1 \in (0, R)$ and
$r_1 \in (0, R)$ and ![]() $C^{\star} \in (0, C_{\mathrm{crit}}(r_1))$ with
$C^{\star} \in (0, C_{\mathrm{crit}}(r_1))$ with ![]() $C_{\mathrm{crit}}(r_1)$ as in (4.2). Then there exist
$C_{\mathrm{crit}}(r_1)$ as in (4.2). Then there exist ![]() $r_\mathrm{min} \in (0,r_1)$,
$r_\mathrm{min} \in (0,r_1)$, ![]() $\theta_\mathrm{max} \gt 0$, κ > 0 and
$\theta_\mathrm{max} \gt 0$, κ > 0 and ![]() $\varepsilon_0 \in (0,1)$ with
$\varepsilon_0 \in (0,1)$ with ![]() $2\kappa\varepsilon_0 \lt \mu$ such that
$2\kappa\varepsilon_0 \lt \mu$ such that
 \begin{align}
\delta := \delta(\varepsilon) := \left(\frac{\varepsilon\kappa(m-1)}{C^{\star} m}\right)^{m-1}
\quad \text{and} \quad
\eta := \eta(\varepsilon) := -C^{\star} \delta^\frac{m}{m-1} + \varepsilon\kappa(R^n - r_1^n + \delta)
\end{align}
\begin{align}
\delta := \delta(\varepsilon) := \left(\frac{\varepsilon\kappa(m-1)}{C^{\star} m}\right)^{m-1}
\quad \text{and} \quad
\eta := \eta(\varepsilon) := -C^{\star} \delta^\frac{m}{m-1} + \varepsilon\kappa(R^n - r_1^n + \delta)
\end{align} are such that ![]() $\eta(\varepsilon) \geq 0$ for all
$\eta(\varepsilon) \geq 0$ for all ![]() $\varepsilon \in (0, \varepsilon_0)$, and that moreover the following holds for all
$\varepsilon \in (0, \varepsilon_0)$, and that moreover the following holds for all ![]() $\varepsilon \in (0, \varepsilon_0)$,
$\varepsilon \in (0, \varepsilon_0)$, ![]() $r_0 \in [r_\mathrm{min}, r_1)$ and
$r_0 \in [r_\mathrm{min}, r_1)$ and ![]() $\theta \in [0, \theta_\mathrm{max}]$:
$\theta \in [0, \theta_\mathrm{max}]$:
Let
 \begin{align}
\underline w(s,t) := \begin{cases}
\mu R^n - \eta - C^{\star}(\rho(t) - s)^\frac{m}{m-1} =: \underline w_{\mathrm{mid}}(s,t) & \text{if } s \lt \rho(t) - \delta \\
\mu R^n - \varepsilon \kappa (R^n - \theta t - s) =: \underline w_{\mathrm{out}}(s,t) & \text{if } s \geq \rho(t) - \delta
\end{cases}
\end{align}
\begin{align}
\underline w(s,t) := \begin{cases}
\mu R^n - \eta - C^{\star}(\rho(t) - s)^\frac{m}{m-1} =: \underline w_{\mathrm{mid}}(s,t) & \text{if } s \lt \rho(t) - \delta \\
\mu R^n - \varepsilon \kappa (R^n - \theta t - s) =: \underline w_{\mathrm{out}}(s,t) & \text{if } s \geq \rho(t) - \delta
\end{cases}
\end{align} for all ![]() $(s,t) \in [r_0^n, R^n]\times[0,\infty)$, where
$(s,t) \in [r_0^n, R^n]\times[0,\infty)$, where ![]() $\rho(t) := r_1^n -\theta t$ for
$\rho(t) := r_1^n -\theta t$ for ![]() $t \in [0,\infty)$. Then
$t \in [0,\infty)$. Then ![]() $\underline w \in C^1([r_0^n, R^n]\times[0,\infty))$ with
$\underline w \in C^1([r_0^n, R^n]\times[0,\infty))$ with ![]() $\partial_s \underline w \geq \varepsilon\kappa \gt 0$ and
$\partial_s \underline w \geq \varepsilon\kappa \gt 0$ and 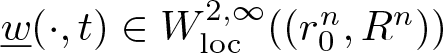 $\underline w(\cdot,t) \in W_\mathrm{loc}^{2,\infty}((r_0^n, R^n))$ for all
$\underline w(\cdot,t) \in W_\mathrm{loc}^{2,\infty}((r_0^n, R^n))$ for all ![]() $t \in [0, \infty)$. If further
$t \in [0, \infty)$. If further
for some ![]() $r_2 \in (r_1, R]$, then
$r_2 \in (r_1, R]$, then
for all ![]() $s \in [r_0^n, r_2^n]\setminus\{\rho(t) - \delta \}$ and
$s \in [r_0^n, r_2^n]\setminus\{\rho(t) - \delta \}$ and ![]() $t\in[0,\infty)$.
$t\in[0,\infty)$.
Proof. Due to ![]() $C^{\star} \lt C_{\mathrm{crit}}(r_1)$, we may fix large κ > 0 as well as small
$C^{\star} \lt C_{\mathrm{crit}}(r_1)$, we may fix large κ > 0 as well as small ![]() $\lambda \in (0,1)$ such that
$\lambda \in (0,1)$ such that
 \begin{align}
C^{\star} \leq \frac{(m-1)\kappa}{m(\kappa + 1)}\left((1-\lambda)\frac{\mu(R^n - r_1^n)(m-1)}{r_1^{2n - 2} n^2}\right)^\frac{1}{m-1}.
\end{align}
\begin{align}
C^{\star} \leq \frac{(m-1)\kappa}{m(\kappa + 1)}\left((1-\lambda)\frac{\mu(R^n - r_1^n)(m-1)}{r_1^{2n - 2} n^2}\right)^\frac{1}{m-1}.
\end{align} We then fix small ![]() $\varepsilon_0 \in (0,1)$ and
$\varepsilon_0 \in (0,1)$ and ![]() $\theta_\mathrm{max} \gt 0$ as well as
$\theta_\mathrm{max} \gt 0$ as well as ![]() $r_\mathrm{min} \in (0, r_1)$ close to r 1 such that
$r_\mathrm{min} \in (0, r_1)$ close to r 1 such that
such that
 \begin{align}
r_1^n - r_0^n \leq \left(\left[\frac{\lambda\mu}{2}(R^n - r_1^n) - \theta_\mathrm{max} - \varepsilon_0\kappa (R^n - r_1^n) \right]\frac{1}{C^{\star}} \right)^\frac{m-1}{m},
\end{align}
\begin{align}
r_1^n - r_0^n \leq \left(\left[\frac{\lambda\mu}{2}(R^n - r_1^n) - \theta_\mathrm{max} - \varepsilon_0\kappa (R^n - r_1^n) \right]\frac{1}{C^{\star}} \right)^\frac{m-1}{m},
\end{align} for all ![]() $r_0 \in [r_\mathrm{min}, r_1)$, and such that the quantities η and δ defined in (4.10) fulfil
$r_0 \in [r_\mathrm{min}, r_1)$, and such that the quantities η and δ defined in (4.10) fulfil
 \begin{align}
\eta \leq \frac{\lambda\mu}{2}(R^n - r_1^n)
\quad \text{and} \quad
\eta = \varepsilon\left(-C^{\star} \left(\frac{\kappa(m-1)}{C^{\star} m}\right)^{m} \varepsilon^{m-1} + \kappa (R^n - r_1^n + \delta) \right) \geq 0
\end{align}
\begin{align}
\eta \leq \frac{\lambda\mu}{2}(R^n - r_1^n)
\quad \text{and} \quad
\eta = \varepsilon\left(-C^{\star} \left(\frac{\kappa(m-1)}{C^{\star} m}\right)^{m} \varepsilon^{m-1} + \kappa (R^n - r_1^n + \delta) \right) \geq 0
\end{align} for all ![]() $\varepsilon \in (0,\varepsilon_0)$, which is possible as δ and thus η converge to 0 as
$\varepsilon \in (0,\varepsilon_0)$, which is possible as δ and thus η converge to 0 as ![]() $\varepsilon \searrow 0$. Henceforth, we fix
$\varepsilon \searrow 0$. Henceforth, we fix ![]() $\varepsilon \in (0, \varepsilon_0)$,
$\varepsilon \in (0, \varepsilon_0)$, ![]() $r_0 \in [r_\mathrm{min}, r_1)$,
$r_0 \in [r_\mathrm{min}, r_1)$, ![]() $r_2 \in (r_1, R]$ and
$r_2 \in (r_1, R]$ and ![]() $\theta \in [0, \theta_\mathrm{max}]$.
$\theta \in [0, \theta_\mathrm{max}]$.
By straightforward calculations, we immediately see that
 \begin{align}
\partial_s \underline w_{\mathrm{mid}}(s,t)
&= \frac{C^{\star} m (\rho(t) - s)^{\frac{1}{m-1}}}{m-1} \gt 0,
\end{align}
\begin{align}
\partial_s \underline w_{\mathrm{mid}}(s,t)
&= \frac{C^{\star} m (\rho(t) - s)^{\frac{1}{m-1}}}{m-1} \gt 0,
\end{align} \begin{align}
\partial_{ss} \underline w_{\mathrm{mid}}(s,t)
&= -\frac{C^{\star} m (\rho(t) - s)^{\frac{1}{m-1}-1}}{(m-1)^2} \lt 0,
\end{align}
\begin{align}
\partial_{ss} \underline w_{\mathrm{mid}}(s,t)
&= -\frac{C^{\star} m (\rho(t) - s)^{\frac{1}{m-1}-1}}{(m-1)^2} \lt 0,
\end{align} \begin{align}
\partial_t \underline w_{\mathrm{mid}}(s,t)
&= -\frac{\rho'(t)C^{\star} m(\rho(t) - s)^{\frac{1}{m-1}}}{m-1}
= \theta \partial_s \underline w_{\mathrm{mid}}(s,t)
\end{align}
\begin{align}
\partial_t \underline w_{\mathrm{mid}}(s,t)
&= -\frac{\rho'(t)C^{\star} m(\rho(t) - s)^{\frac{1}{m-1}}}{m-1}
= \theta \partial_s \underline w_{\mathrm{mid}}(s,t)
\end{align} for all ![]() $s\in[r_0^n, \rho(t) - \delta]$ and
$s\in[r_0^n, \rho(t) - \delta]$ and ![]() $t\in[0,\infty)$ as well as
$t\in[0,\infty)$ as well as
 \begin{align*}
\partial_s \underline w_{\mathrm{out}}(s,t) &= \varepsilon\kappa, \\
\partial_{ss} \underline w_{\mathrm{out}}(s,t) &= 0,\\
\partial_t \underline w_{\mathrm{out}}(s,t) &= \varepsilon\kappa\theta
\end{align*}
\begin{align*}
\partial_s \underline w_{\mathrm{out}}(s,t) &= \varepsilon\kappa, \\
\partial_{ss} \underline w_{\mathrm{out}}(s,t) &= 0,\\
\partial_t \underline w_{\mathrm{out}}(s,t) &= \varepsilon\kappa\theta
\end{align*} for all ![]() $s\in[\rho(t) - \delta, R^n]$ and
$s\in[\rho(t) - \delta, R^n]$ and ![]() $t\in[0,\infty)$. Combined with (4.10), this yields
$t\in[0,\infty)$. Combined with (4.10), this yields
and
 \begin{align*}
\partial_s \underline w_{\mathrm{mid}}(\rho(t) - \delta, t) = \frac{C^{\star} m}{m-1} \delta^{\frac{1}{m-1}} = \varepsilon\kappa = \partial_s \underline w_{\mathrm{out}}(\rho(t) - \delta, t)
\end{align*}
\begin{align*}
\partial_s \underline w_{\mathrm{mid}}(\rho(t) - \delta, t) = \frac{C^{\star} m}{m-1} \delta^{\frac{1}{m-1}} = \varepsilon\kappa = \partial_s \underline w_{\mathrm{out}}(\rho(t) - \delta, t)
\end{align*} for all ![]() $t\in [0,\infty)$. Moreover,
$t\in [0,\infty)$. Moreover, ![]() $\partial_{ss}\underline w_{\mathrm{mid}}$ is continuous on the compact set
$\partial_{ss}\underline w_{\mathrm{mid}}$ is continuous on the compact set ![]() $[r_0^n, \rho(t) - \delta]$ for all
$[r_0^n, \rho(t) - \delta]$ for all ![]() $t\in[0,\infty)$, so that all our desired regularity properties for
$t\in[0,\infty)$, so that all our desired regularity properties for ![]() $\underline w$ are evidently fulfilled.
$\underline w$ are evidently fulfilled.
We will now start the argument proper by plugging ![]() $\underline w_{\mathrm{mid}}$ into the functional
$\underline w_{\mathrm{mid}}$ into the functional ![]() $\mathcal{P}_\varepsilon$ to gain
$\mathcal{P}_\varepsilon$ to gain
 \begin{align*}
\mathcal{P}_\varepsilon \underline w_{\mathrm{mid}} = \partial_s \underline w_{\mathrm{mid}} \left[ \theta - n^2 s^{2-\frac2n}(\partial_s \underline w_{\mathrm{mid}} + \varepsilon)^{m-1}\frac{\partial_{ss} \underline w_{\mathrm{mid}}}{\partial_s \underline w_{\mathrm{mid}}} - \underline w_{\mathrm{mid}} + \mu s \right]
\end{align*}
\begin{align*}
\mathcal{P}_\varepsilon \underline w_{\mathrm{mid}} = \partial_s \underline w_{\mathrm{mid}} \left[ \theta - n^2 s^{2-\frac2n}(\partial_s \underline w_{\mathrm{mid}} + \varepsilon)^{m-1}\frac{\partial_{ss} \underline w_{\mathrm{mid}}}{\partial_s \underline w_{\mathrm{mid}}} - \underline w_{\mathrm{mid}} + \mu s \right]
\end{align*} for all ![]() $s\in[r_0^n, \rho(t) - \delta)$ and
$s\in[r_0^n, \rho(t) - \delta)$ and ![]() $t\in[0,\infty)$.
$t\in[0,\infty)$.
We first estimate the terms originating from taxis to yield
 \begin{align*}
- \underline w_{\mathrm{mid}} + \mu s &= \mu (s-R^n) + \eta + C^{\star}(\rho(t) - s)^{\frac{m}{m-1}} \\
&\leq -\mu (R^n - r_1^n) + \eta + C^{\star}(r_1^n - r_0^n)^{\frac{m}{m-1}}
\end{align*}
\begin{align*}
- \underline w_{\mathrm{mid}} + \mu s &= \mu (s-R^n) + \eta + C^{\star}(\rho(t) - s)^{\frac{m}{m-1}} \\
&\leq -\mu (R^n - r_1^n) + \eta + C^{\star}(r_1^n - r_0^n)^{\frac{m}{m-1}}
\end{align*} for all ![]() $s\in[r_0^n, \rho(t) - \delta)$ and
$s\in[r_0^n, \rho(t) - \delta)$ and ![]() $t\in[0,\infty)$. Applying (4.15) as well as (4.16) to this then results in
$t\in[0,\infty)$. Applying (4.15) as well as (4.16) to this then results in
for all ![]() $s\in[r_0^n, \rho(t) - \delta)$ and
$s\in[r_0^n, \rho(t) - \delta)$ and ![]() $t\in[0,\infty)$.
$t\in[0,\infty)$.
Regarding the diffusive term, we see that (4.17), (4.18), the fact that ![]() $\partial_s \underline w_{\mathrm{mid}} \ge \varepsilon\kappa$ and (4.13) entail that
$\partial_s \underline w_{\mathrm{mid}} \ge \varepsilon\kappa$ and (4.13) entail that
 \begin{align*}
- n^2 s^{2-\frac2n}(\partial_s \underline w_{\mathrm{mid}} + \varepsilon)^{m-1}\frac{\partial_{ss} \underline w_{\mathrm{mid}}}{\partial_s \underline w_{\mathrm{mid}}}
&\le \frac{n^2 s^{2-\frac2n}}{m-1} \left(\frac{\kappa + 1}{\kappa}\partial_s \underline w_{\mathrm{mid}}\right)^{m-1} (\rho(t) - s)^{-1} \\
&\leq \frac{n^2 r_1^{2n - 2}}{m-1} \left(\frac{m(\kappa + 1)}{(m-1)\kappa}C^{\star}\right)^{m-1}
\leq (1-\lambda)\mu(R^n - r_1^n)
\end{align*}
\begin{align*}
- n^2 s^{2-\frac2n}(\partial_s \underline w_{\mathrm{mid}} + \varepsilon)^{m-1}\frac{\partial_{ss} \underline w_{\mathrm{mid}}}{\partial_s \underline w_{\mathrm{mid}}}
&\le \frac{n^2 s^{2-\frac2n}}{m-1} \left(\frac{\kappa + 1}{\kappa}\partial_s \underline w_{\mathrm{mid}}\right)^{m-1} (\rho(t) - s)^{-1} \\
&\leq \frac{n^2 r_1^{2n - 2}}{m-1} \left(\frac{m(\kappa + 1)}{(m-1)\kappa}C^{\star}\right)^{m-1}
\leq (1-\lambda)\mu(R^n - r_1^n)
\end{align*} for all ![]() $s\in[r_0^n, \rho(t) - \delta)$ and
$s\in[r_0^n, \rho(t) - \delta)$ and ![]() $t\in[0,\infty)$. In combination with (4.20), this yields
$t\in[0,\infty)$. In combination with (4.20), this yields
 \begin{align*}
\mathcal{P}_\varepsilon \underline w_{\mathrm{mid}} &\leq \partial_s \underline w_{\mathrm{mid}} \left[ \theta + (1-\lambda)\mu(R^n - r_1^n) - \theta_\mathrm{max} -\varepsilon_0\kappa(R^n - r_1^n) - (1-\lambda)\mu(R^n - r_1^n) \right] \\
&= \partial_s \underline w_{\mathrm{mid}} \left[ \theta - \theta_\mathrm{max} - \varepsilon_0\kappa(R^n - r_1^n) \right]
\leq -\varepsilon\kappa (R^n - r_2^n) \partial_s \underline w_{\mathrm{mid}}
\end{align*}
\begin{align*}
\mathcal{P}_\varepsilon \underline w_{\mathrm{mid}} &\leq \partial_s \underline w_{\mathrm{mid}} \left[ \theta + (1-\lambda)\mu(R^n - r_1^n) - \theta_\mathrm{max} -\varepsilon_0\kappa(R^n - r_1^n) - (1-\lambda)\mu(R^n - r_1^n) \right] \\
&= \partial_s \underline w_{\mathrm{mid}} \left[ \theta - \theta_\mathrm{max} - \varepsilon_0\kappa(R^n - r_1^n) \right]
\leq -\varepsilon\kappa (R^n - r_2^n) \partial_s \underline w_{\mathrm{mid}}
\end{align*} for all ![]() $s\in[r_0^n, \rho(t) - \delta)$ and
$s\in[r_0^n, \rho(t) - \delta)$ and ![]() $t\in[0,\infty)$.
$t\in[0,\infty)$.
We now turn our attention to the linear extension ![]() $\underline w_{\mathrm{out}}$. As its second spatial derivative is always zero, plugging it into the functional
$\underline w_{\mathrm{out}}$. As its second spatial derivative is always zero, plugging it into the functional ![]() $\mathcal{P}_\varepsilon$ allows us to estimate as follows for all
$\mathcal{P}_\varepsilon$ allows us to estimate as follows for all ![]() $s\in(\rho(t) - \delta, r_2^n]$ and
$s\in(\rho(t) - \delta, r_2^n]$ and ![]() $t\in[0,\infty)$ by using (4.14) as well as (4.12):
$t\in[0,\infty)$ by using (4.14) as well as (4.12):
 \begin{align*}
\mathcal{P}_\varepsilon \underline w_{\mathrm{out}} &= \partial_s \underline w_{\mathrm{out}} \left[ \theta - \underline w_{\mathrm{out}} + \mu s \right] \\
&=\partial_s \underline w_{\mathrm{out}} \left[ \theta - \mu(R^n - s) + \varepsilon \kappa(R^n - \theta t - s) \right] \\
&=\partial_s \underline w_{\mathrm{out}} \left[ \theta - (\mu-\varepsilon \kappa)(R^n - s) - \varepsilon \kappa \theta t \right] \\
&\leq\partial_s \underline w_{\mathrm{out}} \left[ \theta - (\mu-\varepsilon_0\kappa)(R^n - r_2^n) \right] \\
&\leq -\varepsilon_0\kappa\partial_s \underline w_{\mathrm{out}}(R^n - r_2^n) \leq -\varepsilon\kappa\partial_s \underline w_{\mathrm{out}}(R^n - r_2^n)
\end{align*}
\begin{align*}
\mathcal{P}_\varepsilon \underline w_{\mathrm{out}} &= \partial_s \underline w_{\mathrm{out}} \left[ \theta - \underline w_{\mathrm{out}} + \mu s \right] \\
&=\partial_s \underline w_{\mathrm{out}} \left[ \theta - \mu(R^n - s) + \varepsilon \kappa(R^n - \theta t - s) \right] \\
&=\partial_s \underline w_{\mathrm{out}} \left[ \theta - (\mu-\varepsilon \kappa)(R^n - s) - \varepsilon \kappa \theta t \right] \\
&\leq\partial_s \underline w_{\mathrm{out}} \left[ \theta - (\mu-\varepsilon_0\kappa)(R^n - r_2^n) \right] \\
&\leq -\varepsilon_0\kappa\partial_s \underline w_{\mathrm{out}}(R^n - r_2^n) \leq -\varepsilon\kappa\partial_s \underline w_{\mathrm{out}}(R^n - r_2^n)
\end{align*}This completes the proof.
To now prove the central result of this subsection, we will use the above family of functions for two consecutive comparison arguments on the approximate level. We begin by comparing with a stationary function ![]() $\underline w$ with θ = 0 on the full interval
$\underline w$ with θ = 0 on the full interval ![]() $(r_0^n, R^n)$ to make use of the uniform boundary value of our approximate solutions at
$(r_0^n, R^n)$ to make use of the uniform boundary value of our approximate solutions at ![]() $s = R^n$. This allows us to show that the support of w at the very least does not expand. We then use this result to establish a similar boundary condition at some point
$s = R^n$. This allows us to show that the support of w at the very least does not expand. We then use this result to establish a similar boundary condition at some point ![]() $r_2^n \lt R^n$ in the interior of the domain to facilitate a second comparison argument on
$r_2^n \lt R^n$ in the interior of the domain to facilitate a second comparison argument on ![]() $(r_0^n, r_2^n)$ with a nonstationary function
$(r_0^n, r_2^n)$ with a nonstationary function ![]() $\underline w$ with θ > 0, which will be key to showing that the support of w in fact actually shrinks. The reason we cannot immediately compare with a nonstationary function in our construction is due to the condition (4.12) on θ, which makes this two-step approach necessary.
$\underline w$ with θ > 0, which will be key to showing that the support of w in fact actually shrinks. The reason we cannot immediately compare with a nonstationary function in our construction is due to the condition (4.12) on θ, which makes this two-step approach necessary.
Lemma 4.3. Let ![]() $r_1 \in (0,R)$ and
$r_1 \in (0,R)$ and ![]() $C \in (0, C_{\mathrm{crit}}(r_1))$ with
$C \in (0, C_{\mathrm{crit}}(r_1))$ with ![]() $C_{\mathrm{crit}}(r_1)$ as in (4.2). Then there exist
$C_{\mathrm{crit}}(r_1)$ as in (4.2). Then there exist ![]() $r_\mathrm{min} \in (0, r_1)$, θ > 0 and λ > 1 such that the following holds for all
$r_\mathrm{min} \in (0, r_1)$, θ > 0 and λ > 1 such that the following holds for all ![]() $r_0 \in [r_\mathrm{min}, r_1)$:
$r_0 \in [r_\mathrm{min}, r_1)$:
If
for all ![]() $s \in [r_0^n, r_1^n]$, then there exists
$s \in [r_0^n, r_1^n]$, then there exists ![]() $T \in (0,T_0)$ such that
$T \in (0,T_0)$ such that
 \begin{align}
w(s,t) \geq \begin{cases}
\mu R^n- \lambda C (r_1^n - \theta t - s)^{\frac{m}{m-1}}& \text{if } s \lt r_1^n - \theta t \\
\mu R^n &\text{if } s \geq r_1^n - \theta t
\end{cases}
\end{align}
\begin{align}
w(s,t) \geq \begin{cases}
\mu R^n- \lambda C (r_1^n - \theta t - s)^{\frac{m}{m-1}}& \text{if } s \lt r_1^n - \theta t \\
\mu R^n &\text{if } s \geq r_1^n - \theta t
\end{cases}
\end{align} for all ![]() $s \in[r_0^n, r_1^n]$ and a.e.
$s \in[r_0^n, r_1^n]$ and a.e. ![]() $t \in [0, T]$.
$t \in [0, T]$.
Proof. We begin by fixing λ > 1 such that
We now fix ![]() $r_\mathrm{min} \in (0,r_1)$,
$r_\mathrm{min} \in (0,r_1)$, ![]() $\theta_\mathrm{max} \gt 0$, κ > 0 and
$\theta_\mathrm{max} \gt 0$, κ > 0 and ![]() $\varepsilon_0 \in (0,1)$ according to Lemma 4.2 and then
$\varepsilon_0 \in (0,1)$ according to Lemma 4.2 and then ![]() $\theta \in (0,\theta_\mathrm{max})$ such that (4.12) holds for
$\theta \in (0,\theta_\mathrm{max})$ such that (4.12) holds for
 \begin{align}
r_2 := \left(\frac{r_1^n + R^n}{2}\right)^\frac1n \in (r_1, R).
\end{align}
\begin{align}
r_2 := \left(\frac{r_1^n + R^n}{2}\right)^\frac1n \in (r_1, R).
\end{align}As (4.21) ensures that
 \begin{align*}
w_0(r_0^n) \geq \mu R^n - C(r_1^n - r_0^n)^{\frac{m}{m-1}} \gt \mu R^n - \frac{\lambda + 1}{2}C(r_1^n - r_0^n)^{\frac{m}{m-1}},
\end{align*}
\begin{align*}
w_0(r_0^n) \geq \mu R^n - C(r_1^n - r_0^n)^{\frac{m}{m-1}} \gt \mu R^n - \frac{\lambda + 1}{2}C(r_1^n - r_0^n)^{\frac{m}{m-1}},
\end{align*} due to 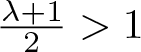 $\frac{\lambda + 1}{2} \gt 1$, there exist
$\frac{\lambda + 1}{2} \gt 1$, there exist ![]() $T \in (0, T_0)$ and
$T \in (0, T_0)$ and ![]() $\varepsilon_1 \in (0,\varepsilon_0]$ such that
$\varepsilon_1 \in (0,\varepsilon_0]$ such that
 \begin{align}
w_\varepsilon(r_0^n, t) \geq \mu R^n - \frac{\lambda + 1}{2}C(r_1^n - r_0^n)^{\frac{m}{m-1}}
\end{align}
\begin{align}
w_\varepsilon(r_0^n, t) \geq \mu R^n - \frac{\lambda + 1}{2}C(r_1^n - r_0^n)^{\frac{m}{m-1}}
\end{align} for all ![]() $t\in[0,T]$ and
$t\in[0,T]$ and ![]() $\varepsilon \in (0, \varepsilon_1)$ by Lemma 2.5 as well as
$\varepsilon \in (0, \varepsilon_1)$ by Lemma 2.5 as well as
 \begin{align}
\delta = \left(\frac{\varepsilon\kappa(m-1)}{C^{\star} m}\right)^{m-1} \lt \frac{r_1^n - r_0^n}{2}
\end{align}
\begin{align}
\delta = \left(\frac{\varepsilon\kappa(m-1)}{C^{\star} m}\right)^{m-1} \lt \frac{r_1^n - r_0^n}{2}
\end{align} for all ![]() $\varepsilon \in (0, \varepsilon_1)$ and
$\varepsilon \in (0, \varepsilon_1)$ and
 \begin{align}
T \lt \max\left\{\frac{r_1^n - r_0^n}{\theta_\mathrm{max}}\left(1 - \left(\frac{2\lambda}{\lambda + 1} \right)^{-\frac{m-1}{m}}\right),\, \frac{r_1^n - r_0^n}{2\theta_\mathrm{max}},\, \frac{R^n - r_1^n}{2\theta_\mathrm{max}}\right\}.
\end{align}
\begin{align}
T \lt \max\left\{\frac{r_1^n - r_0^n}{\theta_\mathrm{max}}\left(1 - \left(\frac{2\lambda}{\lambda + 1} \right)^{-\frac{m-1}{m}}\right),\, \frac{r_1^n - r_0^n}{2\theta_\mathrm{max}},\, \frac{R^n - r_1^n}{2\theta_\mathrm{max}}\right\}.
\end{align} For our first comparison function, let now ![]() $\underline w_{\varepsilon, \mathrm{stat}}$ be as in (4.11) for all
$\underline w_{\varepsilon, \mathrm{stat}}$ be as in (4.11) for all ![]() $\varepsilon \in (0,\varepsilon_1)$ with the parameters as fixed above but θ replaced by 0. Then we gain
$\varepsilon \in (0,\varepsilon_1)$ with the parameters as fixed above but θ replaced by 0. Then we gain
 \begin{align*}
\underline w_{\varepsilon,\mathrm{stat}}(r_0^n, t) = \mu R^n - \eta - \lambda C(r_1^n - r_0^n)^{\frac{m}{m-1}} \leq \mu R^n - \frac{\lambda + 1}{2}C(r_1^n - r_0^n)^{\frac{m}{m-1}} \leq w_\varepsilon(r_0^n, t)
\end{align*}
\begin{align*}
\underline w_{\varepsilon,\mathrm{stat}}(r_0^n, t) = \mu R^n - \eta - \lambda C(r_1^n - r_0^n)^{\frac{m}{m-1}} \leq \mu R^n - \frac{\lambda + 1}{2}C(r_1^n - r_0^n)^{\frac{m}{m-1}} \leq w_\varepsilon(r_0^n, t)
\end{align*} for all ![]() $t \in [0,T]$ and
$t \in [0,T]$ and ![]() $\varepsilon \in (0, \varepsilon_1)$ due to (4.24),
$\varepsilon \in (0, \varepsilon_1)$ due to (4.24), ![]() $\eta \geq 0$,
$\eta \geq 0$, 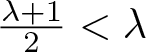 $\frac{\lambda + 1}{2} \lt \lambda$ and (4.25) ensuring that
$\frac{\lambda + 1}{2} \lt \lambda$ and (4.25) ensuring that ![]() $r_0^n \le r_1^n - \delta = \rho(t) - \delta$. We further directly gain that
$r_0^n \le r_1^n - \delta = \rho(t) - \delta$. We further directly gain that
for all ![]() $t \in [0,T]$ and
$t \in [0,T]$ and ![]() $\varepsilon \in (0,\varepsilon_1)$.
$\varepsilon \in (0,\varepsilon_1)$.
Again due to ![]() $\eta \geq 0$, λ > 1 as well as that
$\eta \geq 0$, λ > 1 as well as that 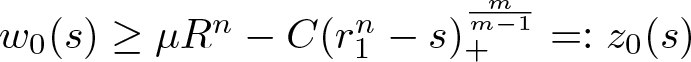 $w_0(s) \geq \mu R^n - C (r_1^n - s)_+^{\frac{m}{m-1}} =: z_0(s)$ for
$w_0(s) \geq \mu R^n - C (r_1^n - s)_+^{\frac{m}{m-1}} =: z_0(s)$ for ![]() $s \in [r_0^n, R^n]$ by (4.21), we see that
$s \in [r_0^n, R^n]$ by (4.21), we see that ![]() $w_0(s) \geq \underline w_{\varepsilon, \mathrm{stat}}(s,0)$ for all
$w_0(s) \geq \underline w_{\varepsilon, \mathrm{stat}}(s,0)$ for all ![]() $s\in[r_0 ^n, r_1^n - \delta]\cup[r_1^n, R^n]$. Moreover, since
$s\in[r_0 ^n, r_1^n - \delta]\cup[r_1^n, R^n]$. Moreover, since ![]() $w_0 \ge z_0$ and
$w_0 \ge z_0$ and ![]() $z_0(r_1^n) \ge \underline w_{\varepsilon, \mathrm{stat}}(r_1^n,0)$, the ordering
$z_0(r_1^n) \ge \underline w_{\varepsilon, \mathrm{stat}}(r_1^n,0)$, the ordering ![]() $w_0(s) \geq \underline w_{\varepsilon, \mathrm{stat}}(s,0)$ in
$w_0(s) \geq \underline w_{\varepsilon, \mathrm{stat}}(s,0)$ in ![]() $[r_1^n - \delta, r_1^n]$ and hence on the full interval
$[r_1^n - \delta, r_1^n]$ and hence on the full interval ![]() $[r_0^n, R^n]$ follows if
$[r_0^n, R^n]$ follows if ![]() $\underline w_{\varepsilon, \mathrm{stat}}(\cdot ,0) - z_0$ is increasing in the former interval. Indeed,
$\underline w_{\varepsilon, \mathrm{stat}}(\cdot ,0) - z_0$ is increasing in the former interval. Indeed,
 \begin{align*}
\partial_s (\underline w_{\varepsilon, \mathrm{stat}}(s,0) - z_0(s))
&= \partial_s \left[ -\varepsilon\kappa(R^n - s) + C (r_1^n - s)^\frac{m}{m-1} \right]
= \varepsilon\kappa - \tfrac{Cm}{m-1} (r_1^n - s)^{\frac{1}{m-1}} \\
&\geq \varepsilon\kappa - \tfrac{Cm}{m-1} \delta^{\frac{1}{m-1}}
= \varepsilon \kappa ( 1 - \tfrac{1}{\lambda})
\geq 0
\end{align*}
\begin{align*}
\partial_s (\underline w_{\varepsilon, \mathrm{stat}}(s,0) - z_0(s))
&= \partial_s \left[ -\varepsilon\kappa(R^n - s) + C (r_1^n - s)^\frac{m}{m-1} \right]
= \varepsilon\kappa - \tfrac{Cm}{m-1} (r_1^n - s)^{\frac{1}{m-1}} \\
&\geq \varepsilon\kappa - \tfrac{Cm}{m-1} \delta^{\frac{1}{m-1}}
= \varepsilon \kappa ( 1 - \tfrac{1}{\lambda})
\geq 0
\end{align*} for ![]() $s \in [r_1^n - \delta, r_1^n]$ by definition of δ in (4.25).
$s \in [r_1^n - \delta, r_1^n]$ by definition of δ in (4.25).
Notably when θ = 0, the condition (4.12) is always trivially fulfilled. Thus Lemma 4.2 ensures that we can apply the comparison result in Lemma 4.1 to wɛ and ![]() $\underline w_{\varepsilon, \mathrm{stat}}$ and thus gain
$\underline w_{\varepsilon, \mathrm{stat}}$ and thus gain ![]() $w_\varepsilon \geq \underline w_{\varepsilon, \mathrm{stat}}$ on
$w_\varepsilon \geq \underline w_{\varepsilon, \mathrm{stat}}$ on ![]() $[r_0^n, R^n]\times[0,T]$. This then directly yields
$[r_0^n, R^n]\times[0,T]$. This then directly yields
 \begin{align}
w_\varepsilon(r_2^n, t) \geq \underline w_{\varepsilon, \mathrm{stat}}(r_2^n, t) = \mu R^n - \varepsilon\kappa \left(\frac{R^n-r_1^n}{2}\right)
\end{align}
\begin{align}
w_\varepsilon(r_2^n, t) \geq \underline w_{\varepsilon, \mathrm{stat}}(r_2^n, t) = \mu R^n - \varepsilon\kappa \left(\frac{R^n-r_1^n}{2}\right)
\end{align} for all ![]() $t\in [0,T]$ and
$t\in [0,T]$ and ![]() $\varepsilon \in (0,\varepsilon_1)$.
$\varepsilon \in (0,\varepsilon_1)$.
For our second comparison argument, we now let
for all ![]() $\varepsilon \in (0,\varepsilon_1)$ with
$\varepsilon \in (0,\varepsilon_1)$ with ![]() $\underline w_\varepsilon$ as in (4.11) with the parameters exactly as chosen at the beginning of this proof (including our choice of θ). We now first observe that
$\underline w_\varepsilon$ as in (4.11) with the parameters exactly as chosen at the beginning of this proof (including our choice of θ). We now first observe that
 \begin{align*}
\underline w_{\varepsilon, \mathrm{shrink}}(r_0^n, t) &= \mu R^n - \eta - \varepsilon\kappa(R^n - r_2^n) - \lambda C(r_1^n - r_0^n - \theta t)^{\frac{m}{m-1}} \\
&\leq \mu R^n - \frac{\lambda + 1}{2}C(r_1^n - r_0^n)^{\frac{m}{m-1}} \\
&\leq w_\varepsilon(r_0^n, t)
\end{align*}
\begin{align*}
\underline w_{\varepsilon, \mathrm{shrink}}(r_0^n, t) &= \mu R^n - \eta - \varepsilon\kappa(R^n - r_2^n) - \lambda C(r_1^n - r_0^n - \theta t)^{\frac{m}{m-1}} \\
&\leq \mu R^n - \frac{\lambda + 1}{2}C(r_1^n - r_0^n)^{\frac{m}{m-1}} \\
&\leq w_\varepsilon(r_0^n, t)
\end{align*} for all ![]() $t\in[0,T]$ and
$t\in[0,T]$ and ![]() $\varepsilon \in (0,\varepsilon_1)$ due to (4.24), (4.26) and
$\varepsilon \in (0,\varepsilon_1)$ due to (4.24), (4.26) and ![]() $\eta \geq 0$, where we have made use of the fact that the conditions on δ and T in (4.25) and (4.26) entail that
$\eta \geq 0$, where we have made use of the fact that the conditions on δ and T in (4.25) and (4.26) entail that ![]() $r_0^n \le r_1^n - \theta T - \delta \le \rho(t) - \delta$. Further,
$r_0^n \le r_1^n - \theta T - \delta \le \rho(t) - \delta$. Further,
 \begin{align*}
\underline w_{\varepsilon, \mathrm{shrink}}(r_2^n, t)
&= \mu R^n - \varepsilon\kappa(R^n - r_2^n) - \varepsilon\kappa\left(R^n - r_2^n - \theta t\right) \\
&= \mu R^n - \varepsilon\kappa\left(R^n - r_1^n - \theta t \right) \\
&\leq \mu R^n - \varepsilon\kappa\left(\frac{R^n - r_1^n}{2} \right) \leq w_\varepsilon(r_2^n, t)
\end{align*}
\begin{align*}
\underline w_{\varepsilon, \mathrm{shrink}}(r_2^n, t)
&= \mu R^n - \varepsilon\kappa(R^n - r_2^n) - \varepsilon\kappa\left(R^n - r_2^n - \theta t\right) \\
&= \mu R^n - \varepsilon\kappa\left(R^n - r_1^n - \theta t \right) \\
&\leq \mu R^n - \varepsilon\kappa\left(\frac{R^n - r_1^n}{2} \right) \leq w_\varepsilon(r_2^n, t)
\end{align*} for all ![]() $t \in [0,T]$ and
$t \in [0,T]$ and ![]() $\varepsilon \in (0,\varepsilon_1)$ due to (4.23), (4.27) and again (4.26). Plugging this second comparison function into
$\varepsilon \in (0,\varepsilon_1)$ due to (4.23), (4.27) and again (4.26). Plugging this second comparison function into ![]() $\mathcal{P}_\varepsilon$, we then see that
$\mathcal{P}_\varepsilon$, we then see that
a.e. on ![]() $[r_0^n, r_2^n]\times[0,T]$ due to Lemma 4.2 and our previous parameter choices. As initial data ordering follows by the same argument as before, this again allows us to apply Lemma 4.1 to gain that
$[r_0^n, r_2^n]\times[0,T]$ due to Lemma 4.2 and our previous parameter choices. As initial data ordering follows by the same argument as before, this again allows us to apply Lemma 4.1 to gain that
on ![]() $[r_0^n, r_1^n]\times[0,T]$. As
$[r_0^n, r_1^n]\times[0,T]$. As ![]() $\underline w_{\varepsilon, \mathrm{shrink}}$ converges pointwise to
$\underline w_{\varepsilon, \mathrm{shrink}}$ converges pointwise to
 \begin{align*}
(s,t) \mapsto \begin{cases}
\mu R^n- \lambda C (r_1^n - \theta t - s)^{\frac{m}{m-1}}& \text{if } s \lt r_1^n - \theta t \\
\mu R^n &\text{if } s \geq r_1^n - \theta t
\end{cases}
\end{align*}
\begin{align*}
(s,t) \mapsto \begin{cases}
\mu R^n- \lambda C (r_1^n - \theta t - s)^{\frac{m}{m-1}}& \text{if } s \lt r_1^n - \theta t \\
\mu R^n &\text{if } s \geq r_1^n - \theta t
\end{cases}
\end{align*} as ![]() $\varepsilon \searrow 0$, we then gain our desired result due to the pointwise convergence property in (3.2).
$\varepsilon \searrow 0$, we then gain our desired result due to the pointwise convergence property in (3.2).
4.2. Case of support expansion
We now treat the support expansion case by showing that w lies above a function of the type seen in (4.1) with a positive coefficient for θ under an appropriate assumption at t = 0.
In this case, we again move the extension point in our approximate comparison functions slightly to the left of ![]() $r_1^n + \theta t$ when compared to (4.1) but also modify said functions in such a fashion as to still allow for a constant extension. This allows us to similarly work around the potential singularity of the second derivative at
$r_1^n + \theta t$ when compared to (4.1) but also modify said functions in such a fashion as to still allow for a constant extension. This allows us to similarly work around the potential singularity of the second derivative at ![]() $r_1^n + \theta t$ as before while ensuring that the extension part is still a supersolution.
$r_1^n + \theta t$ as before while ensuring that the extension part is still a supersolution.
Lemma 4.4. Let ![]() $r_1 \in (0, R)$ and
$r_1 \in (0, R)$ and ![]() $C^{\star} \gt C_{\mathrm{crit}}(r_1)$ with
$C^{\star} \gt C_{\mathrm{crit}}(r_1)$ with ![]() $C_{\mathrm{crit}}(r_1)$ as in (4.2). Then there exists
$C_{\mathrm{crit}}(r_1)$ as in (4.2). Then there exists ![]() $r_\mathrm{min}\in(0,r_1)$, θ > 0 as well as
$r_\mathrm{min}\in(0,r_1)$, θ > 0 as well as ![]() $\varepsilon_0 \in (0,1)$ such that the following holds for all
$\varepsilon_0 \in (0,1)$ such that the following holds for all ![]() $r_0 \in [r_\mathrm{min}, r_1)$ and
$r_0 \in [r_\mathrm{min}, r_1)$ and ![]() $\varepsilon \in (0, \varepsilon_0)$:
$\varepsilon \in (0, \varepsilon_0)$:
Let
 \begin{align}
\overline w(s,t) := \begin{cases}
\mu R^n - C^{\star}(\rho(t) - s)^{\frac{m}{m-1}} + \varepsilon (\rho(t) - s) =: \overline w_{\mathrm{mid}}(s,t) & \text{if } s \lt \rho(t) - \delta \\
\mu R^n + \frac{\delta \varepsilon}{m} =: \overline w_{\mathrm{out}}(s,t) & \text{if } s \geq \rho(t) - \delta
\end{cases}
\end{align}
\begin{align}
\overline w(s,t) := \begin{cases}
\mu R^n - C^{\star}(\rho(t) - s)^{\frac{m}{m-1}} + \varepsilon (\rho(t) - s) =: \overline w_{\mathrm{mid}}(s,t) & \text{if } s \lt \rho(t) - \delta \\
\mu R^n + \frac{\delta \varepsilon}{m} =: \overline w_{\mathrm{out}}(s,t) & \text{if } s \geq \rho(t) - \delta
\end{cases}
\end{align} for all ![]() $(s,t) \in [r_0^n, R^n]\times[0,T^{\star}]$ with
$(s,t) \in [r_0^n, R^n]\times[0,T^{\star}]$ with 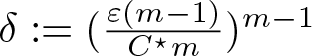 $\delta := (\frac{\varepsilon(m-1)}{C^{\star} m})^{m-1}$,
$\delta := (\frac{\varepsilon(m-1)}{C^{\star} m})^{m-1}$, ![]() $\rho(t) := r_1^n + \theta t$ and
$\rho(t) := r_1^n + \theta t$ and 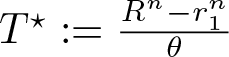 $T^{\star} := \frac{R^n - r_1^n}{\theta}$.
$T^{\star} := \frac{R^n - r_1^n}{\theta}$.
Then ![]() $\overline w \in C^1([r_0^n, R^n]\times[0,T^{\star}])$ with
$\overline w \in C^1([r_0^n, R^n]\times[0,T^{\star}])$ with ![]() $\partial_s \overline w \geq 0$ and
$\partial_s \overline w \geq 0$ and 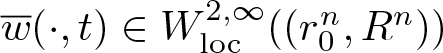 $\overline w(\cdot,t) \in W_\mathrm{loc}^{2,\infty}((r_0^n, R^n))$ for all
$\overline w(\cdot,t) \in W_\mathrm{loc}^{2,\infty}((r_0^n, R^n))$ for all ![]() $t \in [0, T^{\star}]$. Further,
$t \in [0, T^{\star}]$. Further,
for all ![]() $s \in [r_0^n, R^n]\setminus\{\rho(t) - \delta \}$ and
$s \in [r_0^n, R^n]\setminus\{\rho(t) - \delta \}$ and ![]() $t\in[0,T^{\star}]$.
$t\in[0,T^{\star}]$.
Proof. We first fix ![]() $r_\mathrm{min} \in (0, r_1)$ as well as small θ > 0 such that
$r_\mathrm{min} \in (0, r_1)$ as well as small θ > 0 such that
 \begin{align}
C^{\star} \geq \frac{m-1}{m}\left(\frac{(\mu R^n - \mu r_0^n + 2\theta)(m-1)}{r_0^{2n - 2} n^2}\right)^\frac{1}{m-1}
\end{align}
\begin{align}
C^{\star} \geq \frac{m-1}{m}\left(\frac{(\mu R^n - \mu r_0^n + 2\theta)(m-1)}{r_0^{2n - 2} n^2}\right)^\frac{1}{m-1}
\end{align} for all ![]() $r_0 \in [r_\mathrm{min}, r_1)$. We then further note that the definition of
$r_0 \in [r_\mathrm{min}, r_1)$. We then further note that the definition of ![]() $T^{\star}$ entails that
$T^{\star}$ entails that
Finally, we let 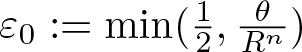 $\varepsilon_0 := \min(\frac12, \frac{\theta}{R^n})$ and fix
$\varepsilon_0 := \min(\frac12, \frac{\theta}{R^n})$ and fix ![]() $\varepsilon \in (0, \varepsilon_0)$ as well as
$\varepsilon \in (0, \varepsilon_0)$ as well as ![]() $r_0 \in [r_\mathrm{min}, r_1)$.
$r_0 \in [r_\mathrm{min}, r_1)$.
By straightforward calculations, we immediately see that
 \begin{align*}
\partial_s \overline w_{\mathrm{mid}}(s,t) &= \frac{C^{\star} m(\rho(t) - s)^{\frac{1}{m-1}}}{m-1} - \varepsilon, \\
\partial_{ss} \overline w_{\mathrm{mid}}(s,t) &= -\frac{C^{\star} m(\rho(t) - s)^{\frac{1}{m-1}-1}}{(m-1)^2}, \\
\partial_t \overline w_{\mathrm{mid}}(s,t) &= -\frac{C^{\star} m \rho'(t)(\rho(t) - s)^{\frac{1}{m-1}}}{m-1} + \varepsilon \rho'(t) = -\theta \partial_s \overline w_{\mathrm{mid}}(s,t)
\end{align*}
\begin{align*}
\partial_s \overline w_{\mathrm{mid}}(s,t) &= \frac{C^{\star} m(\rho(t) - s)^{\frac{1}{m-1}}}{m-1} - \varepsilon, \\
\partial_{ss} \overline w_{\mathrm{mid}}(s,t) &= -\frac{C^{\star} m(\rho(t) - s)^{\frac{1}{m-1}-1}}{(m-1)^2}, \\
\partial_t \overline w_{\mathrm{mid}}(s,t) &= -\frac{C^{\star} m \rho'(t)(\rho(t) - s)^{\frac{1}{m-1}}}{m-1} + \varepsilon \rho'(t) = -\theta \partial_s \overline w_{\mathrm{mid}}(s,t)
\end{align*} for all ![]() $s\in[r_0^n, \rho(t) - \delta)$ and
$s\in[r_0^n, \rho(t) - \delta)$ and ![]() $t\in[0,T^{\star}]$. As the definition of δ warrants that
$t\in[0,T^{\star}]$. As the definition of δ warrants that
 \begin{align*}
\overline w_{\mathrm{mid}}(\rho(t) - \delta,t) &= \mu R^n - C^{\star} \delta^{\frac{m}{m-1}} + \varepsilon \delta
= \mu R^n + (\varepsilon - C^{\star} \delta^\frac{1}{m-1})\delta
= \mu R^n + \frac{\delta \varepsilon}{m} \\
& = \overline w_{\mathrm{out}}(\rho(t) - \delta, t)
\end{align*}
\begin{align*}
\overline w_{\mathrm{mid}}(\rho(t) - \delta,t) &= \mu R^n - C^{\star} \delta^{\frac{m}{m-1}} + \varepsilon \delta
= \mu R^n + (\varepsilon - C^{\star} \delta^\frac{1}{m-1})\delta
= \mu R^n + \frac{\delta \varepsilon}{m} \\
& = \overline w_{\mathrm{out}}(\rho(t) - \delta, t)
\end{align*}and
 \begin{align*}
\partial_s \overline w_{\mathrm{mid}}(\rho(t) - \delta,t) = \frac{C^{\star} m}{m-1} \delta^{\frac{1}{m-1}} - \varepsilon = 0 = \partial_s \overline w_{\mathrm{out}}(\rho(t) - \delta, t),
\end{align*}
\begin{align*}
\partial_s \overline w_{\mathrm{mid}}(\rho(t) - \delta,t) = \frac{C^{\star} m}{m-1} \delta^{\frac{1}{m-1}} - \varepsilon = 0 = \partial_s \overline w_{\mathrm{out}}(\rho(t) - \delta, t),
\end{align*} for all ![]() $t\in[0,T^{\star}]$, and as
$t\in[0,T^{\star}]$, and as ![]() $\partial_{ss}\overline w_{\mathrm{mid}}$ is continuous on the compact set
$\partial_{ss}\overline w_{\mathrm{mid}}$ is continuous on the compact set ![]() $[r_0^n, \rho(t) - \delta]$ for all
$[r_0^n, \rho(t) - \delta]$ for all ![]() $t\in[0,T^{\star}]$, our desired regularity properties for
$t\in[0,T^{\star}]$, our desired regularity properties for ![]() $\overline w$ are immediately evident. Moreover, since
$\overline w$ are immediately evident. Moreover, since ![]() $\partial_{ss} \overline w_{\mathrm{mid}}(s,t) \lt 0$, we can directly see that
$\partial_{ss} \overline w_{\mathrm{mid}}(s,t) \lt 0$, we can directly see that ![]() $\partial_{s} \overline w_{\mathrm{mid}}(s,t) \gt 0$ for all
$\partial_{s} \overline w_{\mathrm{mid}}(s,t) \gt 0$ for all ![]() $s\in[r_0^n, \rho(t) - \delta)$ and
$s\in[r_0^n, \rho(t) - \delta)$ and ![]() $t\in[0,T^{\star}]$.
$t\in[0,T^{\star}]$.
Plugging the above into the parabolic operator ![]() $\mathcal{P}_\varepsilon$, we then see that
$\mathcal{P}_\varepsilon$, we then see that
 \begin{align*}
\mathcal{P}_\varepsilon \overline w_{\mathrm{mid}} = \partial_s \overline w_{\mathrm{mid}} \left[ -\theta - n^2 s^{2-\frac2n}(\partial_s \overline w_{\mathrm{mid}} + \varepsilon)^{m-1}\frac{\partial_{ss} \overline w_{\mathrm{mid}}}{\partial_s \overline w_{\mathrm{mid}}} - \overline w_{\mathrm{mid}} + \mu s \right]
\end{align*}
\begin{align*}
\mathcal{P}_\varepsilon \overline w_{\mathrm{mid}} = \partial_s \overline w_{\mathrm{mid}} \left[ -\theta - n^2 s^{2-\frac2n}(\partial_s \overline w_{\mathrm{mid}} + \varepsilon)^{m-1}\frac{\partial_{ss} \overline w_{\mathrm{mid}}}{\partial_s \overline w_{\mathrm{mid}}} - \overline w_{\mathrm{mid}} + \mu s \right]
\end{align*} for all ![]() $s\in[r_0^n, \rho(t) - \delta)$ and
$s\in[r_0^n, \rho(t) - \delta)$ and ![]() $t\in[0,T^{\star}]$. We now begin by deriving that
$t\in[0,T^{\star}]$. We now begin by deriving that
 \begin{align}
- \overline w_{\mathrm{mid}} + \mu s &= \mu(s - R^n) + C^{\star}(\rho(t) - s)^{\frac{m}{m-1}} - \varepsilon(\rho(t) - s) \nonumber\\
&\geq -\mu (R^n - r_0^n) - \varepsilon \rho(t) \nonumber\\
&\geq -\mu (R^n - r_0^n) - \varepsilon_0 R^n
\geq -\mu (R^n - r_0^n) - \theta
\end{align}
\begin{align}
- \overline w_{\mathrm{mid}} + \mu s &= \mu(s - R^n) + C^{\star}(\rho(t) - s)^{\frac{m}{m-1}} - \varepsilon(\rho(t) - s) \nonumber\\
&\geq -\mu (R^n - r_0^n) - \varepsilon \rho(t) \nonumber\\
&\geq -\mu (R^n - r_0^n) - \varepsilon_0 R^n
\geq -\mu (R^n - r_0^n) - \theta
\end{align} for all ![]() $s\in[r_0^n, \rho(t) - \delta)$ and
$s\in[r_0^n, \rho(t) - \delta)$ and ![]() $t\in[0,T^{\star}]$ by our choice of ɛ 0. Now considering the diffusion term, we further gather that
$t\in[0,T^{\star}]$ by our choice of ɛ 0. Now considering the diffusion term, we further gather that
 \begin{align*}
- n^2 s^{2-\frac2n}(\partial_s \overline w_{\mathrm{mid}} + \varepsilon)^{m-1}\frac{\partial_{ss} \overline w_{\mathrm{mid}}}{\partial_s \overline w_{\mathrm{mid}}}
&= \frac{n^2 s^{2-\frac2n}}{m-1}\left(\frac{C^{\star} m}{m-1}\right)^{m}\frac{(\rho(t) - s)^{\frac{1}{m-1}} }{\frac{C^{\star} m}{m-1}(\rho(t) - s)^{\frac{1}{m-1}} - \varepsilon} \\
&\geq \frac{n^2 r_0^{2n-2}}{m-1}\left(\frac{C^{\star} m}{m-1}\right)^{m-1}
\geq \mu (R^n - r_0^n) + 2\theta
\end{align*}
\begin{align*}
- n^2 s^{2-\frac2n}(\partial_s \overline w_{\mathrm{mid}} + \varepsilon)^{m-1}\frac{\partial_{ss} \overline w_{\mathrm{mid}}}{\partial_s \overline w_{\mathrm{mid}}}
&= \frac{n^2 s^{2-\frac2n}}{m-1}\left(\frac{C^{\star} m}{m-1}\right)^{m}\frac{(\rho(t) - s)^{\frac{1}{m-1}} }{\frac{C^{\star} m}{m-1}(\rho(t) - s)^{\frac{1}{m-1}} - \varepsilon} \\
&\geq \frac{n^2 r_0^{2n-2}}{m-1}\left(\frac{C^{\star} m}{m-1}\right)^{m-1}
\geq \mu (R^n - r_0^n) + 2\theta
\end{align*} for all ![]() $s\in[r_0^n, \rho(t) - \delta)$ and
$s\in[r_0^n, \rho(t) - \delta)$ and ![]() $t\in[0,T^{\star}]$ due to (4.30) and thus that
$t\in[0,T^{\star}]$ due to (4.30) and thus that
by combining this with (4.31). Since ![]() $\overline w_{\mathrm{out}}$ is constant and hence fulfils
$\overline w_{\mathrm{out}}$ is constant and hence fulfils ![]() $\mathcal{P}_\varepsilon \overline w_{\mathrm{out}} = 0$, we obtain (4.29).
$\mathcal{P}_\varepsilon \overline w_{\mathrm{out}} = 0$, we obtain (4.29).
Using the above family of comparison functions, our desired result then follows from Lemma 4.1, which importantly does not require ![]() $\overline w$ to be strictly increasing.
$\overline w$ to be strictly increasing.
Lemma 4.5. Let ![]() $r_1 \in (0,R)$ and
$r_1 \in (0,R)$ and ![]() $C \gt C_{\mathrm{crit}}(r_1)$ with
$C \gt C_{\mathrm{crit}}(r_1)$ with ![]() $C_{\mathrm{crit}}(r_1)$ as in (4.2). Then there exist
$C_{\mathrm{crit}}(r_1)$ as in (4.2). Then there exist ![]() $r_\mathrm{min} \in (0, r_1)$, θ > 0 as well as λ > 1, such that the following holds for all
$r_\mathrm{min} \in (0, r_1)$, θ > 0 as well as λ > 1, such that the following holds for all ![]() $r_0 \in [r_\mathrm{min},r_1)$:
$r_0 \in [r_\mathrm{min},r_1)$:
If
for all ![]() $s \in [r_0^n, r_1^n]$, then there exists
$s \in [r_0^n, r_1^n]$, then there exists ![]() $T \in (0,T_0)$ such that
$T \in (0,T_0)$ such that
 \begin{align}
w(s,t) \leq \begin{cases}
\mu R^n- \frac{C}{\lambda} (r_1^n + \theta t - s)^{\frac{m}{m-1}}& \text{if } s \lt r_1^n + \theta t, \\
\mu R^n &\text{if } s \geq r_1^n + \theta t
\end{cases}
\end{align}
\begin{align}
w(s,t) \leq \begin{cases}
\mu R^n- \frac{C}{\lambda} (r_1^n + \theta t - s)^{\frac{m}{m-1}}& \text{if } s \lt r_1^n + \theta t, \\
\mu R^n &\text{if } s \geq r_1^n + \theta t
\end{cases}
\end{align} for all ![]() $s \in[r_0^n, R^n]$ and a.e.
$s \in[r_0^n, R^n]$ and a.e. ![]() $t \in [0, T]$.
$t \in [0, T]$.
Proof. We begin by fixing λ > 1 such that
 \begin{align*}
C^{\star} := \frac{C}{\lambda} \gt C_{\mathrm{crit}}(r_1).
\end{align*}
\begin{align*}
C^{\star} := \frac{C}{\lambda} \gt C_{\mathrm{crit}}(r_1).
\end{align*} We now let 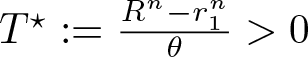 $T^{\star} := \frac{R^n-r_1^n}{\theta} \gt 0$ and fix
$T^{\star} := \frac{R^n-r_1^n}{\theta} \gt 0$ and fix ![]() $r_\mathrm{min} \in (0,r_1)$, θ > 0 as well as
$r_\mathrm{min} \in (0,r_1)$, θ > 0 as well as ![]() $\varepsilon_0 \in (0,1)$ according to Lemma 4.4. As (4.32) ensures that
$\varepsilon_0 \in (0,1)$ according to Lemma 4.4. As (4.32) ensures that
 \begin{align*}
w_0(r_0^n) \leq \mu R^n - C(r_1^n - r_0^n)^{\frac{m}{m-1}} \lt \mu R^n - \frac{2C}{\lambda + 1}(r_1^n - r_0^n)^{\frac{m}{m-1}}
\end{align*}
\begin{align*}
w_0(r_0^n) \leq \mu R^n - C(r_1^n - r_0^n)^{\frac{m}{m-1}} \lt \mu R^n - \frac{2C}{\lambda + 1}(r_1^n - r_0^n)^{\frac{m}{m-1}}
\end{align*} due to 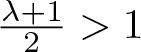 $\frac{\lambda + 1}{2} \gt 1$, Lemma 2.5 allows us to fix
$\frac{\lambda + 1}{2} \gt 1$, Lemma 2.5 allows us to fix ![]() $T \in (0,\min(T_0,T^{\star}) )$ and
$T \in (0,\min(T_0,T^{\star}) )$ and ![]() $\varepsilon_1 \in (0,\varepsilon_0]$ such that
$\varepsilon_1 \in (0,\varepsilon_0]$ such that
 \begin{align}
w_\varepsilon(r_0^n,t) \leq \mu R^n - \frac{2C}{\lambda+1}(r_1^n - r_0^n)^{\frac{m}{m-1}}
\end{align}
\begin{align}
w_\varepsilon(r_0^n,t) \leq \mu R^n - \frac{2C}{\lambda+1}(r_1^n - r_0^n)^{\frac{m}{m-1}}
\end{align} for all ![]() $t\in [0,T]$ and
$t\in [0,T]$ and ![]() $\varepsilon \in (0,\varepsilon_1)$ as well as
$\varepsilon \in (0,\varepsilon_1)$ as well as
 \begin{align}
\delta = \left(\frac{\varepsilon(m-1)}{C^{\star} m}\right)^{m-1} \lt r_1^n - r_0^n
\end{align}
\begin{align}
\delta = \left(\frac{\varepsilon(m-1)}{C^{\star} m}\right)^{m-1} \lt r_1^n - r_0^n
\end{align} for all ![]() $\varepsilon \in (0, \varepsilon_1)$ and
$\varepsilon \in (0, \varepsilon_1)$ and
 \begin{align}
T \leq \frac{r_1^n - r_0^n}{\theta}\left[\left( \frac{2\lambda}{\lambda + 1} \right)^\frac{m-1}{m} - 1\right].
\end{align}
\begin{align}
T \leq \frac{r_1^n - r_0^n}{\theta}\left[\left( \frac{2\lambda}{\lambda + 1} \right)^\frac{m-1}{m} - 1\right].
\end{align} Let now ![]() $\overline w_\varepsilon$ with
$\overline w_\varepsilon$ with ![]() $\mathcal{P}_\varepsilon \overline w_\varepsilon \geq 0$ be as in (4.28) for all
$\mathcal{P}_\varepsilon \overline w_\varepsilon \geq 0$ be as in (4.28) for all ![]() $\varepsilon \in (0,\varepsilon_1)$ with the parameters as chosen above. We then check the necessary ordering at the left boundary as follows:
$\varepsilon \in (0,\varepsilon_1)$ with the parameters as chosen above. We then check the necessary ordering at the left boundary as follows:
 \begin{align*}
\overline w_\varepsilon(r_0^n, t) &= \mu R^n - \frac{C}{\lambda}(r_1^n - r_0^n + \theta t)^{\frac{m}{m-1}} + \varepsilon(r_1^n - r_0^n + \theta t) \\
&\geq \mu R^n - \frac{2C}{\lambda+1}(r_1^n - r_0^n)^{\frac{m}{m-1}} \geq w_\varepsilon(r_0^n, t)
\end{align*}
\begin{align*}
\overline w_\varepsilon(r_0^n, t) &= \mu R^n - \frac{C}{\lambda}(r_1^n - r_0^n + \theta t)^{\frac{m}{m-1}} + \varepsilon(r_1^n - r_0^n + \theta t) \\
&\geq \mu R^n - \frac{2C}{\lambda+1}(r_1^n - r_0^n)^{\frac{m}{m-1}} \geq w_\varepsilon(r_0^n, t)
\end{align*} for all ![]() $t \in [0,T]$ and
$t \in [0,T]$ and ![]() $\varepsilon \in (0,\varepsilon_1)$ due to (4.34) and (4.36) as well as (4.35) ensuring that
$\varepsilon \in (0,\varepsilon_1)$ due to (4.34) and (4.36) as well as (4.35) ensuring that ![]() $r_0^n \lt r_1^n - \delta \leq \rho(t) - \delta$. Regarding the right boundary point, we observe that
$r_0^n \lt r_1^n - \delta \leq \rho(t) - \delta$. Regarding the right boundary point, we observe that
 \begin{align*}
\overline w_\varepsilon(R^n, t) = \mu R^n + \frac{\delta\varepsilon}{m} \geq \mu R^n
\end{align*}
\begin{align*}
\overline w_\varepsilon(R^n, t) = \mu R^n + \frac{\delta\varepsilon}{m} \geq \mu R^n
\end{align*} for all ![]() $t \in [0,T]$ and
$t \in [0,T]$ and ![]() $\varepsilon \in (0,\varepsilon_1)$, where
$\varepsilon \in (0,\varepsilon_1)$, where 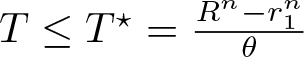 $T \leq T^{\star} = \frac{R^n-r_1^n}{\theta}$ ensures that
$T \leq T^{\star} = \frac{R^n-r_1^n}{\theta}$ ensures that ![]() $R^n \geq \rho(t) \gt \rho(t) - \delta$. Moreover, we can conclude that
$R^n \geq \rho(t) \gt \rho(t) - \delta$. Moreover, we can conclude that
 \begin{align*}
\overline w_\varepsilon(s, 0) = \mu R^n - \frac{C}{\lambda}(r_1^n - s)^{\frac{m}{m-1}} + \varepsilon(r_1^n - s) \geq \mu R^n - C(r_1^n - s)^{\frac{m}{m-1}} \geq w_0(s)
\end{align*}
\begin{align*}
\overline w_\varepsilon(s, 0) = \mu R^n - \frac{C}{\lambda}(r_1^n - s)^{\frac{m}{m-1}} + \varepsilon(r_1^n - s) \geq \mu R^n - C(r_1^n - s)^{\frac{m}{m-1}} \geq w_0(s)
\end{align*} for all ![]() $s \in [r_0^n, r_1^n-\delta)$ due to λ > 1 and (4.32) as well as
$s \in [r_0^n, r_1^n-\delta)$ due to λ > 1 and (4.32) as well as
 \begin{align*}
\overline w_\varepsilon(s, 0) = \mu R^n + \frac{\delta \varepsilon}{m} \geq \mu R^n\geq w_0(s)
\end{align*}
\begin{align*}
\overline w_\varepsilon(s, 0) = \mu R^n + \frac{\delta \varepsilon}{m} \geq \mu R^n\geq w_0(s)
\end{align*} for all ![]() $s \in [r_1^n-\delta, R^n]$ since by construction
$s \in [r_1^n-\delta, R^n]$ since by construction ![]() $w_0 \leq \mu R^n$. Thus, we can now employ Lemma 4.1 to gain that
$w_0 \leq \mu R^n$. Thus, we can now employ Lemma 4.1 to gain that
for all ![]() $(s,t) \in [r_0^n, R^n] \times [0,T]$. Using that
$(s,t) \in [r_0^n, R^n] \times [0,T]$. Using that ![]() $\overline w_\varepsilon$ converges pointwise to
$\overline w_\varepsilon$ converges pointwise to
 \begin{align*}
(s,t) \mapsto \begin{cases}
\mu R^n - \frac{C}{\lambda}(r_1^n + \theta t - s)^\frac{m}{m-1} &\text{if } s \lt \theta t + r_1^n, \\
\mu R^n & \text{if } s \geq \theta t + r_1^n
\end{cases}
\end{align*}
\begin{align*}
(s,t) \mapsto \begin{cases}
\mu R^n - \frac{C}{\lambda}(r_1^n + \theta t - s)^\frac{m}{m-1} &\text{if } s \lt \theta t + r_1^n, \\
\mu R^n & \text{if } s \geq \theta t + r_1^n
\end{cases}
\end{align*} as ![]() $\varepsilon \searrow 0$, we then gain our desired result due to the pointwise convergence property in (3.2).
$\varepsilon \searrow 0$, we then gain our desired result due to the pointwise convergence property in (3.2).
5. Proof of Theorem 1.1
Having now established all necessary prerequisites, we can start putting the puzzle pieces together to prove our main theorem.
Proof of Theorem 1.1
We begin by treating the support shrinking case. We thus now assume that (1.4) holds for some positive ![]() $A \lt A_{\mathrm{crit}}$ and
$A \lt A_{\mathrm{crit}}$ and ![]() $r_0 \in (0,r_1)$. The definitions of
$r_0 \in (0,r_1)$. The definitions of ![]() $A_{\mathrm{crit}}$ and
$A_{\mathrm{crit}}$ and ![]() $C_{\mathrm{crit}}$ in (1.3) and (4.2) entail
$C_{\mathrm{crit}}$ in (1.3) and (4.2) entail
 \begin{align*}
A_{\mathrm{crit}} \frac{n^{-\frac{1}{m-1}}r_1^{-\frac{(n-1)m}{m-1}} r_1^{n-1}(m-1)}{m} = C_{\mathrm{crit}}(r_1),
\end{align*}
\begin{align*}
A_{\mathrm{crit}} \frac{n^{-\frac{1}{m-1}}r_1^{-\frac{(n-1)m}{m-1}} r_1^{n-1}(m-1)}{m} = C_{\mathrm{crit}}(r_1),
\end{align*}so that by replacing r 0 with an r 0 sufficiently close to r 1, if necessary, we may assume
 \begin{align*}
C := \frac{A n^{-\frac{1}{m-1}}r_0^{-\frac{(n-1)m}{m-1}} r_1^{n-1}(m-1)}{m} \lt C_{\mathrm{crit}}(r_1).
\end{align*}
\begin{align*}
C := \frac{A n^{-\frac{1}{m-1}}r_0^{-\frac{(n-1)m}{m-1}} r_1^{n-1}(m-1)}{m} \lt C_{\mathrm{crit}}(r_1).
\end{align*} Let now ![]() $r_\mathrm{min} \in (0,r_1)$ be as provided by Lemma 4.3 for the constant C fixed above. Let then further
$r_\mathrm{min} \in (0,r_1)$ be as provided by Lemma 4.3 for the constant C fixed above. Let then further ![]() $
r_\star := \max(r_\mathrm{min}, r_0)
$. Lemma 3.1 then yields that
$
r_\star := \max(r_\mathrm{min}, r_0)
$. Lemma 3.1 then yields that
for all ![]() $s \in (r_\star^n, r_1^n)$, which in turn allows us to apply Lemma 4.3 to further fix
$s \in (r_\star^n, r_1^n)$, which in turn allows us to apply Lemma 4.3 to further fix ![]() $T \in (0,T_0)$, λ > 0 and θ > 0 such that (4.22) holds for all
$T \in (0,T_0)$, λ > 0 and θ > 0 such that (4.22) holds for all ![]() $s \in [r_\star^n, r_1^n]$ and a.e.
$s \in [r_\star^n, r_1^n]$ and a.e. ![]() $t \in [0,T]$. If we complement this lower bound with the fact that
$t \in [0,T]$. If we complement this lower bound with the fact that ![]() $w(s,t) \leq \mu R^n$ for all
$w(s,t) \leq \mu R^n$ for all ![]() $s \in [r_\star^n, R^n]$ and a.e.
$s \in [r_\star^n, R^n]$ and a.e. ![]() $t \in [0,T]$ due to (3.3), we gain that
$t \in [0,T]$ due to (3.3), we gain that
for all ![]() $s \in [r_1^n - \theta t, R^n]$ and a.e.
$s \in [r_1^n - \theta t, R^n]$ and a.e. ![]() $t\in[0,T]$. This implies that
$t\in[0,T]$. This implies that
 \begin{align*}
0 = w(R^n, t) - w(r_1^n - \theta t, t) = n\int^{R}_{(r_1^n - \theta t)^\frac{1}{n}} \rho^{n-1} u(\rho,t) \,\mathrm{d}\rho
\end{align*}
\begin{align*}
0 = w(R^n, t) - w(r_1^n - \theta t, t) = n\int^{R}_{(r_1^n - \theta t)^\frac{1}{n}} \rho^{n-1} u(\rho,t) \,\mathrm{d}\rho
\end{align*} for a.e. ![]() $t \in [0,T]$. Given the a.e. nonnegativity of u and positivity of ρ, it thus follows that
$t \in [0,T]$. Given the a.e. nonnegativity of u and positivity of ρ, it thus follows that
for a.e. 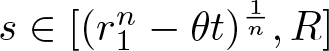 $s \in [(r_1^n - \theta t)^\frac{1}{n}, R]$ and a.e.
$s \in [(r_1^n - \theta t)^\frac{1}{n}, R]$ and a.e. ![]() $t\in[0, T]$ and hence
$t\in[0, T]$ and hence
 \begin{align*}
\sup (\operatorname{ess}\operatorname{supp} u(\cdot, t)) \leq (r_1^n - \theta t)^\frac{1}{n}
\qquad \text{for a.e.}\ t \in (0,T).
\end{align*}
\begin{align*}
\sup (\operatorname{ess}\operatorname{supp} u(\cdot, t)) \leq (r_1^n - \theta t)^\frac{1}{n}
\qquad \text{for a.e.}\ t \in (0,T).
\end{align*} As here  $(r_1^n - \theta t)^\frac{1}{n} - r_1 \le -\frac1n r_1^{1-n} \theta t =: -\zeta t$ for all
$(r_1^n - \theta t)^\frac{1}{n} - r_1 \le -\frac1n r_1^{1-n} \theta t =: -\zeta t$ for all ![]() $t \in (0, T)$ by the mean value theorem, this implies (1.5).
$t \in (0, T)$ by the mean value theorem, this implies (1.5).
By combining Lemma 3.1 and Lemma 4.5 while assuming (1.6), in a very similar fashion to the argument above, we can gain another set of C > 0, ![]() $r_\star\in(0,r_1)$,
$r_\star\in(0,r_1)$, ![]() $T \in (0,T_0)$, λ > 0 and θ > 0 such that (4.33) holds for all
$T \in (0,T_0)$, λ > 0 and θ > 0 such that (4.33) holds for all ![]() $s \in [r_\star^n, R^n]$ and a.e.
$s \in [r_\star^n, R^n]$ and a.e. ![]() $t \in [0, T]$. This implies that
$t \in [0, T]$. This implies that
 \begin{align*}
w(R^n, t) - w(s,t) \geq \mu R^n - \mu R^n + \frac{C}{\lambda} (r_1^n + \theta t - s)^\frac{m}{m-1} \gt 0
\end{align*}
\begin{align*}
w(R^n, t) - w(s,t) \geq \mu R^n - \mu R^n + \frac{C}{\lambda} (r_1^n + \theta t - s)^\frac{m}{m-1} \gt 0
\end{align*}and thus
 \begin{align*}
n\int^{R}_{s^\frac{1}{n}} \rho^{n-1} u(\rho,t) \,\mathrm{d}\rho \gt 0
\end{align*}
\begin{align*}
n\int^{R}_{s^\frac{1}{n}} \rho^{n-1} u(\rho,t) \,\mathrm{d}\rho \gt 0
\end{align*} for all ![]() $s \in (r_\star^n, r_1^n + \theta t)$ and a.e.
$s \in (r_\star^n, r_1^n + \theta t)$ and a.e. ![]() $t \in [0,T]$. Therefore, for all
$t \in [0,T]$. Therefore, for all ![]() $s \in (r_\star^n, r_1^n + \theta t)$ and a.e.
$s \in (r_\star^n, r_1^n + \theta t)$ and a.e. ![]() $t \in [0,T]$, there must exist a set
$t \in [0,T]$, there must exist a set 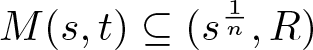 $M(s, t) \subseteq (s^\frac{1}{n}, R)$ of positive measure such that
$M(s, t) \subseteq (s^\frac{1}{n}, R)$ of positive measure such that ![]() $u(\cdot, t) \gt 0$ on
$u(\cdot, t) \gt 0$ on ![]() $M(s, t)$. This directly implies
$M(s, t)$. This directly implies  $\sup(\operatorname{ess}\operatorname{supp} u(\cdot, t)) \geq s^\frac1n$ for all
$\sup(\operatorname{ess}\operatorname{supp} u(\cdot, t)) \geq s^\frac1n$ for all ![]() $s \in (r_\star^n, r_1^n + \theta t)$ and a.e.
$s \in (r_\star^n, r_1^n + \theta t)$ and a.e. ![]() $t \in [0,T]$ and hence
$t \in [0,T]$ and hence
 \begin{align*}
\sup (\operatorname{ess}\operatorname{supp} u(\cdot, t)) \geq (r_1^n + \theta t)^\frac{1}{n}
\qquad \text{for a.e.}\ t \in (0,T).
\end{align*}
\begin{align*}
\sup (\operatorname{ess}\operatorname{supp} u(\cdot, t)) \geq (r_1^n + \theta t)^\frac{1}{n}
\qquad \text{for a.e.}\ t \in (0,T).
\end{align*} By a final application of the mean value theorem, we conclude that (1.7) holds for 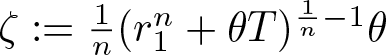 $\zeta := \frac1n (r_1^n + \theta T)^{\frac1n-1} \theta$.
$\zeta := \frac1n (r_1^n + \theta T)^{\frac1n-1} \theta$.
Acknowledgements
The second author acknowledges support of the Deutsche Forschungsgemeinschaft in the context of the project Fine structures in interpolation inequalities and application to parabolic problems, Project Number 462888149.